✍个人博客：https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
📣专栏定位：为学习吴恩达机器学习视频的同学提供的随堂笔记。
📚专栏简介：在这个专栏，我将整理吴恩达机器学习视频的所有内容的笔记，方便大家参考学习。
📝视频地址：吴恩达机器学习系列课程
❤️如果有收获的话，欢迎点赞👍收藏📁，您的支持就是我创作的最大动力💪

二、单变量线性回归

常用表达符号：

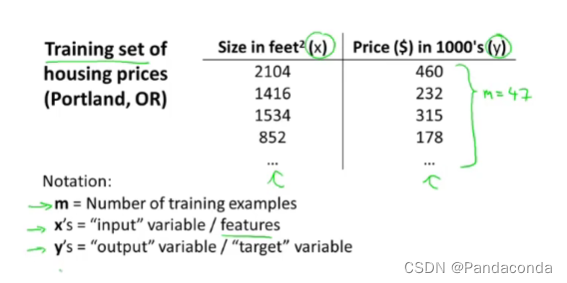
假设函数（Hypthesis）

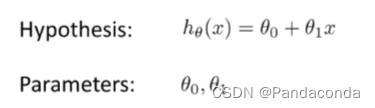
假设函数通过找到最优的两个参数，从而去获得一个与数据最佳拟合曲线。

1. 代价函数

• 定义：通过**代价函数（cost function）**得到的值，来获得最优解，值越小代表准确度越高。
• 所以我们要通过找到代价函数的最小值，从而得到其对应的参数值，然后得到最佳拟合曲线。

平方误差代价函数（The squared error dost function）

其中在算式前面除以二是方便后续的求导计算，此函数可以解决大部分的回归问题。

这就是我们的线性回归模型。

而我们可以通过简化假设函数，从而去更好理解代价函数背后的含义。

其代价函数图像如下：

上面我们可以知道当参数等于1时，代价函数的值最小，所以将参数带回假设函数的方程中，我们就可以得到一条与数据能够最佳拟合的曲线。如果参数更多的话，就会更加复杂，下面是两个参数的三维图像：

小结

因此，对于回归问题，我们只用归结为求出代价函数的最小值即可，下面就是我线性回归的目标函数。

2. 梯度下降

• 定义：我们会得到初始化的参数，然后通过改变参数不断地去寻找更小的J值。

• 注意
  • 梯度下降的其中一个特点为，你可能会因为初始位置的偏差而得到两个不同的局部最优解，就如下图

梯度下降算法（Gradient Descent Algorithm）

赋值与等号

• ：=在计算机中代表赋值，即将b赋值给a
• =在计算机中代表真假判定，即判断a是否等于b

算式中α用来控制下降的速率，值越大则梯度下降的越快，但是α的值不能太大或太小，原因如下：

• 如果α太小，则需要很多很多步才能到达最低点。
• 如果α太大，可能会导致无法收敛甚至发散，它可能会越过最低点。

在梯度下降算法中，参数要同时更新，即下图图左侧为正确操作，右侧为不正确操作。

在算式最右边的那一块导数部分是J函数对参数求偏导即为切线斜率，详解如下：

• 如果所选参数在J函数曲线中切线斜率为正，那么导数块部分也为正，即参数会减去一个正值，从图像上来看，参数减小的方向往左即是往曲线最低点方向进行。
• 如果所选参数在J函数曲线中切线斜率为负，那么导数块部分也为负，即参数会减去一个负值，也就是加上一个正值，从图像上来看，参数增大的方向往右即也是往曲线最低点方向进行。

所以通过图像可知，当运算已经达到了局部最低点，切线斜率为零，参数也不会再改变了，如下图：

小结

综上所述，当α处于正常范围内并且不变的话，函数任然可以找到局部最低点，因为越靠近最低点，切线斜率会越小直至等于零，所以它减小的幅度会越来越小，直至到达局部最低点。

3. 线性回归的梯度下降

• 当学习完线性回归模型（下图右侧）与梯度下降算法（下图左侧）后，就是要解决两者结合的问题

现在我们将线性回归模型带入梯度下降算法中计算，首先来计算导数这一部分，求出我们参数的导数部分表达式。

最后，带回到参数的正式表达式，就如下所示：

在梯度下降函数中，我们可能会因为初始值不同得到不同的局部最优值，但是在线性回归的代价函数中，总会得到一个最小并且唯一的最小值，即会得到一个凸函数（convex function），如下图所示：

所以只要用线性回归函数的梯度下降，最终总会得到一个全局的最优解，他没有其他的局部最优解。

而这个梯度下降问题就如下图所示，不断地改变参数值，从而找到最好拟合数据的曲线。

小结

总的来说，我们上面所用到的算法如下：

Batch 梯度下降法

意思是在每一步梯度下降时，它都会遍历了整个训练集的样本。

这是目前来说，我们第一个所学习的机器算法。