点云配准

实验目标

• 任务一：将两个形状、大小相同的点云进行配准，进而估计两个点云之间的位姿。
• 任务二：将一些列深度图反向投影得到点云，经过配准后，得到每个深度图之间的位姿变换，并将相应的点云融合到一起。

编译运行环境

项目 Python3 编写，实现 RANSAC 配准和 ICP 配准，用到 open3d 和 numpy 库。运行 python main.py src.ply tgt.ply save_path.ply ，读取源点云 src.ply，目标点云 tgt.ply，保存路径 save_path.ply。会显示三张图，分别为原始点云（源点云用红色标注，目标点云用绿色标注）、粗配准结果、精配准结果。

算法设计

任务一和任务二的主要思路一致，都是先对点云进行降采样、滤波后计算点云特征信息（包括法向量、特征直方图、以及后续特征匹配需要的若干特征），再利用提取的特征使用 RANSAC 的方法进行粗配准，最后使用 ICP 的方法进行精配准。

特征提取

【PCL学习笔记】之快速点特征直方图FPFH - pcl::FPFHSignature33 - Eba_

使用 FPFH（Fast Point Feature Histogram）算法。PFH（Point Feature Histogram）算法提取没给点邻域内两两点对间几何特征（一些角度信息），绘制直方图。FPFH 保留了 PFH 的大部分信息，但忽略了相邻点之间的计算，而是按照距离的反比将一个邻域内的点的直方图加权得到 33 维向量，效率更高。尝试了使用 PCA 进行降维以提高后续特征匹配速度，发现作用不大，遂舍弃。

粗配准

使用 RANSAC 的方法，总而言之就是对于源点云中的三个点，去“蒙”他们和目标点云中的那几个点相对应，然后计算变换矩阵，检验其优劣。简要流程如下：

1. 在源点云中随机选择 3 个点。
2. 分别查找他们在目标点云中特征向量最接近的点。这里的“接近”是欧式距离意义下的，查询数据结构使用 KD 树。
3. 计算两个三角形之间的变换矩阵。其实就是按照 ICP 精配准的过程，求最小二乘法意义下的最优变换矩阵。
4. 求出源点云在此变换之后的点云，计算其与目标点云的重合度（定义为源点云中阈值半径内存在目标点的点的个数）。
5. 回到1，重复若干次，维护并返回重合度最高的变换。

实际编码中，由于 4 中 KD 树查询速度比较慢（33 维空间中接近于 $O(n)$），因提高在 1、2 中选择三角形对的质量是一个好的做法。这里三角形对的质量一是指他们匹配的可能性，二是通过他们计算出的变换矩阵是否准确。可以想到的方法有很多，比如三角形的边不能太短、两个三角形的对应边长不能差太多、优先选择特征向量远离均值的点等等。我的实现中采用了前两种。此外，在降采样后的点云上配准也可以提高效率。

精配准

【点云精配准】Iterative Closest Point（ICP）- Forrest Ding

具体推导过程就不赘述了。

深度图融合

上面的算法可以较好地完成对形状、大小相同的点云配准。但是，如果直接应用在深度图上，会出现匹配不上的问题（下面为 single-depth 匹配结果的俯视图）：

这是因为 ICP 为每个源点云中的点，都从目标点云中找到一个距离最近的点和它匹配。但在深度图中，两个点云存在很多点本来就是不匹配的。如果强行令他们匹配，那么在最小二乘法的意义下最优解就是上图这样，一个点云被移动到了另一个的“中央”位置。

改进方法就是，对于源点云中的一个点，如果在目标点云中不存在和它的距离小于某个阈值的点，那么在此次迭代中就不考虑该点。同时，这个阈值随着迭代的进行不断减小的（有下限），这样就使得配准越来越精细。

关键代码

RANSAC

实现中还涉及两个细节。

一是匹配阈值设为多大合适？由于不同的数据具有不同的尺寸，因此本算法实现了自适应的过程。我们想要得到点云（在某个表面上的）平均距离。考虑体素下采样 oldPcd.voxel_down_sample(voxel_size)，采样到一定程度后，点云密集处的平均距离就是 voxel_size。因此将 RANSAC 的匹配阈值设置为 2.5 * voxel_size。

二是如何判断两个三角形的差距？代码中如果对应边长度之差大于 lengthThreshold * 长度平均值。

这样，50 次有效采样就能计算出很好的转移矩阵。从下面的效果可以看出，即使是粗配准的效果就很好了。

def RANSAC():
    maxCount = 0
    jisuan=0
    j = 0
    print("RANSACing...")
    while True:
        j += 1
        // 随机选取三个点
        srcCorr = random.sample(range(srcNum), 3)
        // 如果某两个点距离太近，舍弃
        if not notTooClose3([srcPoints[x] for x in srcCorr]):
            continue
            
        // KD 树特征匹配
        tgtCorr = []
        for id in srcCorr:
            k, idx, dis2 = tgtFpfhKDT.search_knn_vector_xd(srcFpfh[id], knn=1)
            tgtCorr.append(random.choice(idx[0]))
            
        // 如果两个三角形差距太大，也舍弃
        if True in [farAway(srcPoints[i[0]] - srcPoints[j[0]], 
                            tgtPoints[i[1]] - tgtPoints[j[1]]) 
                    for i in zip(srcCorr, tgtCorr) 
                    for j in zip(srcCorr, tgtCorr)]:
            continue
        jisuan += 1
        
        // 得到变换矩阵
        R, T = calculateTrans(np.array([srcPoints[i] for i in srcCorr]), 
                              np.array([tgtPoints[i] for i in tgtCorr]))
        A = np.transpose((R @ srcPoints.T) + np.tile(T, (1, srcNum)))
        
        //计算匹配数
        count = 0
        for point in range(0, srcNum, 1):
            k, idx, dis2 = tgtKDT.search_hybrid_vector_3d(A[point], 
                                                          radius=fitThreshold, max_nn=1)
            count += k
        
        // 更新最大匹配
        if count > maxCount:
            maxCount = count
            bestR, bestT = R, T
        if jisuan > 50 and j > 1000:
            break
        
    print("RANSAC calculated %d times, maximum matches: %d" % (jisuan, maxCount))
    return bestR, bestT

ICP

def ICP(src, tgt):
    limit = fitThreshold
    retR = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
    retT = np.array([[0], [0], [0]])
    trace = []
    for _ in range(400):
        tgtCorr = []
        srcCorr = []
        // 筛选距离近的点对
        for point in src:
            k, idx, dis2 = tgtKDT.search_knn_vector_3d(point, knn=1)
            if dis2[0] < (limit)**2:
                srcCorr.append(point)
                tgtCorr.append(tgt[idx[0]])
        trace.append([limit, len(srcCorr)])
        R, T = calculateTrans(np.array(srcCorr), np.array(tgtCorr))
        retR = R @ retR
        retT = R @ retT + T
        src = np.transpose((R @ src.T) + np.tile(T, (1, srcNum)))
        // 阈值的衰减
        limit = (limit - fitThreshold/1.5) * 0.95 + fitThreshold/1.5
        // 自适应过程，如果匹配点对不变化说明算法收敛，退出迭代
        if len(trace) > 50 and len(set([x[1] for x in trace[-20:]])) == 1:	
            break
    print("ICP trace is:", trace)
    return retR, retT

效果

在所有的测试数据中，算法都能够取得令人满意的结果，这里选择 airplane、person 以及 single-depth 三组数据进行展示。另外，如果直接对原始数据进行配准，会导致源点云和目标点云完全重合，只会显示单一的颜色，不利于观察效果。因此算法对每组数据都做了适量的下采样之后进行配准，因此能够看出是两个点云匹配的结果。

airplane:

配准前：

粗配准：

精配准：

person:

配准前：

粗配准：

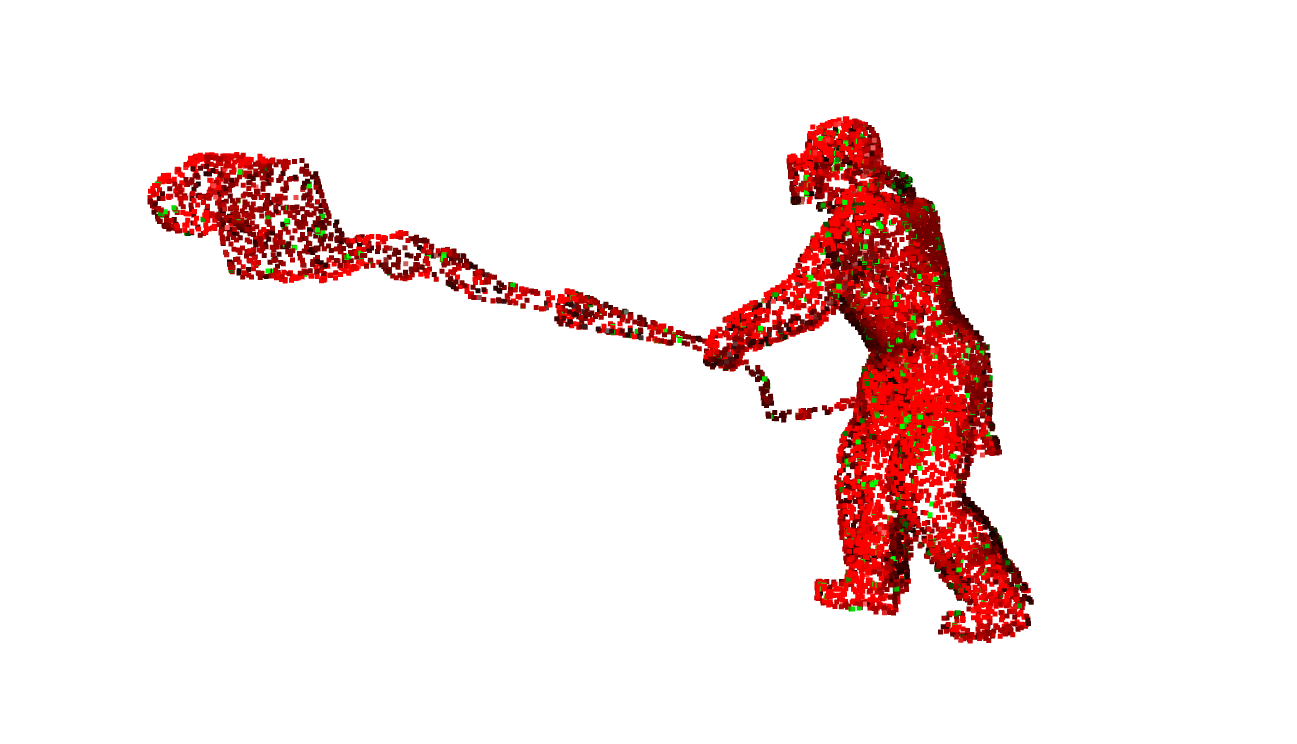
精配准：

single-depth:

配准前（降采样后）：

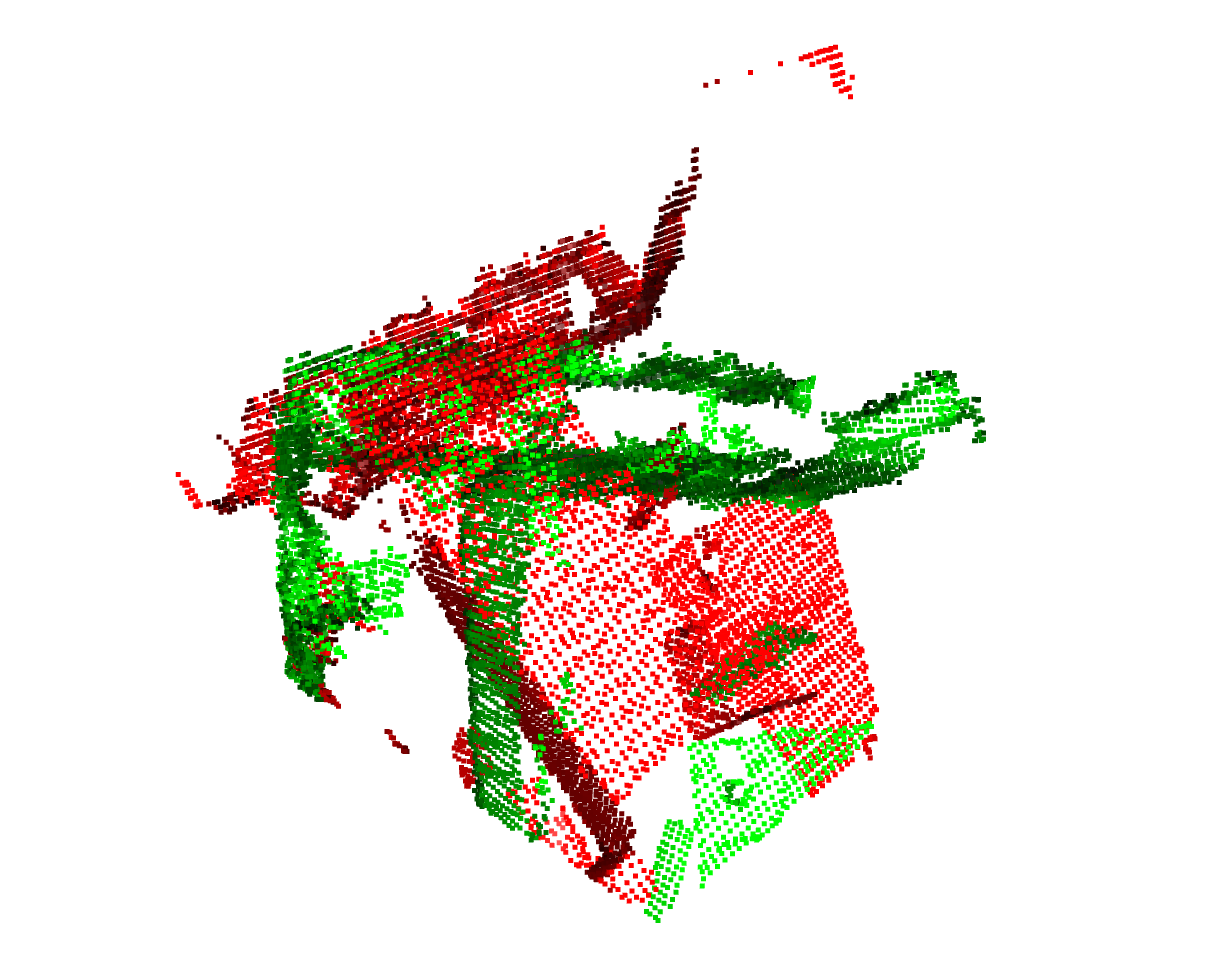
粗配准（降采样后）：

精配准：