一、元组tuple定义

为什么需要元组

列表是可以修改的，如果想要传递的信息不被篡改，列表就不适合了

元组和列表一样，都是可以封装多个不同类型的元素在内

最大的不同点在于：

元祖一旦定义完成，就不可修改

所以，当我们需要在程序内封装数据，但不希望封装的数据被篡改，元组就非常合适了

元组的定义： 定义元组使用小括号，且用逗号隔开，数据可以是不同类型。

注意：元组只有一个元素，这个数据后面要加逗号；否则类型是str 而不是tuple

元组也支持嵌套，元组也可以利用下表索引取出元素 

# 定义元祖

t1 = (1,'jerk',True)

t2 = ()

t3 =tuple()

print(f"t1的类型是：{type(t1)},内容是：{t1}")

print(f"t2的类型是：{type(t2)},内容是：{t2}")

print(f"t3的类型是：{type(t3)},内容是：{t3}")

# 定义单个元素的元素 后面带逗号，否则不是tuple类型

t4 = ('one',)

print(f"t4的类型是：{type(t4)},内容是：{t4}")

# 元组的嵌套

t5 = (1,2,3,t4,(6,7))

print(f"t5的类型是：{type(t5)},内容是：{t5}")

# 元组也可以利用下表索引取出元素 取出 t5中的7

element = t5[4][1]

print(f"从嵌套t5中取出的数据是：{element}")

二、元组的相关操作

# 元组的遍历：while

index = 0

while index < len(t8):

    element = t8[index]

    print(f"通过while遍历的元组有元素：{element}")

    index += 1



# 元组的遍历：for

for element1 in t8:

    print(f"通过for遍历的元组有元素：{element1}")

注意事项：

• 不可以修改元祖的内容，否则会直接报错

• 可以修改元组内的list的内容（修改元素、增加、删除、反转等）

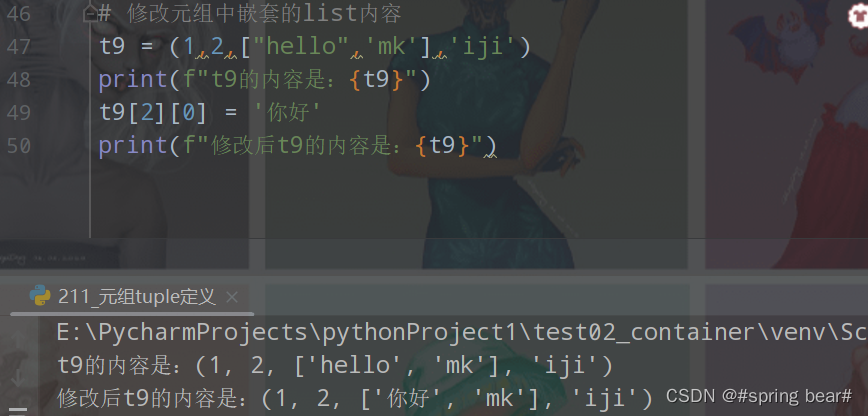
总结元组特点：

• 可以容纳多个数据

• 可以容纳不同类型的数据（嵌套）

• 数据是有序存储的（下标索引）

• 允许重复数据存在

• 不允许修改元组（增删改），但是可以修改嵌套在其中的list的内容

• 支持while/for循环

多数特性和list一致，不同点在于不可修改的特性