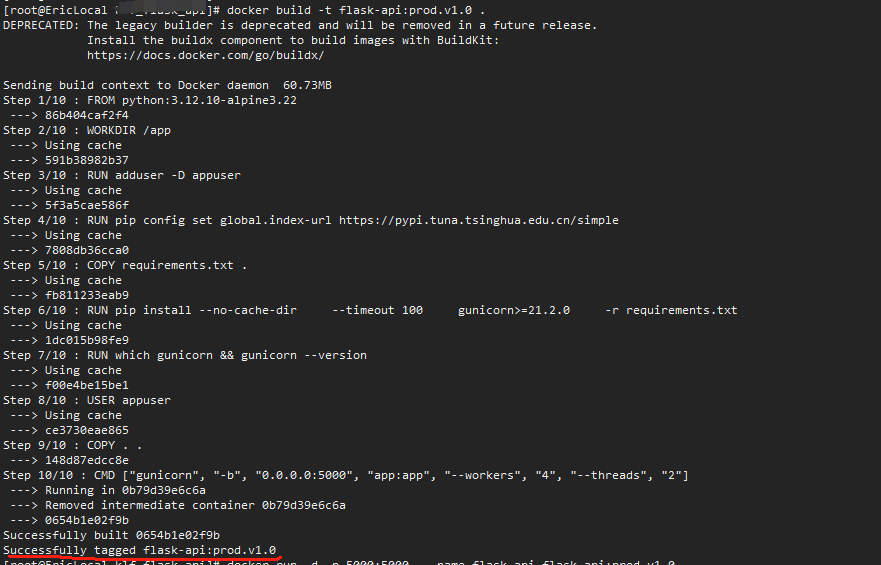
前言
byd这组题纯靠感觉是吧…^_^¦¦¦
b题赛时举了无数个例子都没想明白,然后一直卡到结束,后面题都没看到,结果补题的时候c题d题直接秒了…-_-||
A. Energy Crystals
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
void solve()
{
int x;
cin>>x;
priority_queue<int,vector<int>,greater<int>>pq;
for(int i=0;i<3;i++)
{
pq.push(0);
}
int ans=0;
while(!pq.empty())
{
int cur=pq.top();
pq.pop();
ans++;
if(!pq.empty())
{
int next=pq.top()*2+1;
if(next<x)
{
pq.push(next);
}
}
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}上来这个题就花了半个小时,但好歹观察了半天观察出来了……
思路就是准备一个小根堆,维护三个晶体能量的最小值,然后在往上增加的过程中最优解肯定是让三者的最小值增加到能增加到的最大值。接着就是每次拿堆顶元素,让最小值往上跳,操作数ans+1。之后若堆不为空,就每次往第二小,即当前堆顶的两倍加一跳。若比目标x小,就再加入堆顶,等着后续去跳。否则就当作直接跳到x,不往堆里加即可。
B. Fibonacci Cubes
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int MAXN=10+5;
//数列值
vector<int>fib(MAXN);
void build(int n)
{
fib[1]=1;
fib[2]=2;
for(int i=3;i<=n;i++)
{
fib[i]=fib[i-1]+fib[i-2];
}
}
void solve()
{
int n,m;
cin>>n>>m;
//生成斐波那契数列
build(n);
for(int i=0,w,l,h;i<m;i++)
{
//重点:斐波那契数列的性质
//…… 13 8 5 3 2 1
//对于最大的立方体,只有长宽高都大于等于的时候才能放
//若底面较大,高度不够了
// 因为13=8+5,所以只需要判断剩余底面上的空间是否大于8,之后8和5可以并列放在13旁边
// 又因为5=3+2,8=5+3,所以在边长为5的立方体上,必然可以放下3和2,此时5+3高度正好8
// 最后在边长为2的立方体上必然可以放下1
//若高度较大,底面不够了
// 同样因为13=8+5,所以只要上方高度大于等于8,就存在8×13×13的区域
// 此时和上个情况相同,必然可以放下后续所有的
//题目本身已经定义了哪面是底!!!!!
cin>>w>>l>>h;
if(w<l)//让w更大
{
swap(w,l);
}
if(h<fib[n]||l<fib[n]||w<fib[n])//放不下
{
cout<<0;
}
else if(w>=fib[n]+fib[n-1])//底面上放下fib[n]后存在fib[n-1]×fib[n]×fib[n]的区域
{
cout<<1;
}
else if(h>=fib[n]+fib[n-1])//高度满足
{
cout<<1;
}
else
{
cout<<0;
}
}
cout<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}这个题的重点是斐波那契数列的性质对放置的影响。虽然赛时想到了要联系斐波那契数列的性质,但真没想到这个结论……
首先,这个题里已经明确给出了哪条边是长宽高,不需要自己判断!!!(nnd赛时没看到这个,一直在想如何放置之后判断长宽高,浪费了不少时间……)读入数据之后,可以默认w大于l,如果相反就交换。然后,因为肯定从最大的开始放,所以若三条边中有一条比这个最大值还小,那直接就是不可能放出来,直接输出0即可。
之后的思路是重点,举个例子,当n=6时,此时数列从大到小为13,8,5,3,2,1。此时可以分底面比较大、高度比较小和高度比较大、底面比较小两种情况讨论。
对于第一种情况,在底面上放下13×13×13后,因为高度比较小,所以只能在这个正方体旁边的底面上放后续立方体。而根据斐波那契数列的性质,13=8+5,所以考虑极限情况,即若底面剩余的空间只能放下8×8×8的,那么这个立方体和5×5×5的立方体必然可以整齐地贴在13×13×13的立方体旁边。然后因为8=5+3,所以即使底面剩余的空间放不下了,3×3×3的立方体仍可以放在5×5×5的立方体上,和8×8×8的立方体的高对齐。同理,2×2×2的立方体也能贴着3×3×3的立方体正好和5×5×5的立方体的边对齐,最后1×1×1的也可以放在2×2×2的上面和3×3×3的高对齐。
第二种情况里,因为底面比较小,所以极限情况是在放下13×13×13的立方体后底面放不下剩下的立方体了。同样因为13=8+5,所以若剩余高度能放下8×8×8的,那么5×5×5的就能靠着8×8×8的和13×13×13的边对齐。之后还是因为8=5+3,所以3×3×3的可以放在5×5×5的上方和8×8×8的高对齐。接下来的过程就和第一种情况类似了。
所以,只需要判断底面两边的最大值w或者高度h是否大于等于fib[n]+fib[n-1]即可,满足的话就必然可以放下,输出1,否则就是0。
C. Equal Values
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
void solve()
{
int n;
cin>>n;
vector<int>a(n+1);
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
ll ans=1e18;
for(int i=1;i<=n;i++)
{
ll left=(i-1)*(ll)a[i];
while(i+1<=n&&a[i+1]==a[i])
{
i++;
}
ll right=(n-i)*(ll)a[i];
ans=min(ans,left+right);
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}蚌埠住了,感觉cd比b简单多了……
这个题直接观察测试用例就能发现方法了。要想把整个数组刷成一样的,那么对于每个数,要把数组刷成和当前数一样就是往左刷一次再往右刷一次。而为了让刷的次数减小,所以若遇到几个连续相等的数,那就让最左侧的往左刷,最右侧的往右刷,中间天然相等的部分就可以不用刷了。
所以方法就是来到每个数时先统计一下往左刷的代价,再跳到这一段连续相等的最后一个数,计算一下往右刷的代价,最后统计代价left和right之和的最小值即可。
D. Creating a Schedule
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
void solve()
{
int n,m;
cin>>n>>m;
vector<int>c(m);
for(int i=0;i<m;i++)
{
cin>>c[i];
}
sort(c.begin(),c.end());
//这代码太抽象了
for(int i=0,p=0;i<n;i+=2,p++)
{
for(int j=0;j<((n-i)>1?2:1);j++)
{
bool t=j%2;
for(int k=0;k<6;k++)
{
cout<<(t?c[p]:c[m-p-1])<<" ";
t=!t;
}
cout<<endl;
}
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}这个题真属于是贪心到极致了……
因为随便输出一种即可,观察测试用例就能发现,只需要让这n个班级两两一组,每组在两个教室交替着上课即可。又因为要求跨越的楼层最大,所以对于每一组两个班,让他们在序号最大和最小的两个教室来回走即可。
所以方法就是先对教室从小到大排序,然后枚举这n个班级,注意每次i+=2往后跳两个表示一组两个班级。接着当剩余班级大于1时,就说明可以合并成一组,那就循环两次,每次交替输出去上课的教室。而对于每一组去上课的教室,就是设置一个指针p,每过完一组p往后跳一步。当前组上课的两个教室就是p位置的教室和m-p-1位置的教室,即剩下空闲的教室的最大最小值。
要注意的就是若只剩下一个班级,那只需要循环一次即可。
E. Changing the String
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
void solve()
{
int n,q;
cin>>n>>q;
string s;
cin>>s;
//需要考虑操作的先后次序!!
//字符类型转数字方便操作
vector<int>b(q);
for(int i=0;i<q;i++)
{
char x,y;
cin>>x>>y;
b[i]=(x-'a')*10+y-'a';//转数字
}
//字符串转数字
vector<int>a(n);
for(int i=0;i<n;i++)
{
a[i]=s[i]-'a';
}
//用set存第几次操作
vector<set<int>>c(23);
for(int i=0;i<q;i++)
{
c[b[i]].insert(i);
}
//从高位到低位考虑
for(int i=0;i<n;i++)
{
//是'a'不改
if(a[i]==0)
{
continue;
}
//是'b'
if(a[i]==1)
{
//能一步转'a'
if(!c[10].empty())
{
a[i]=0;
c[10].erase(c[10].begin());//删第一次
}
else if(!c[12].empty()&&!c[20].empty())//不能一步转 -> "bc""ca"
{
auto iter=c[20].lower_bound(*c[12].begin());//删"bc"后的第一个"ca"
if(iter!=c[20].end())//后续有"ca"才改
{
a[i]=0;
c[12].erase(c[12].begin());
c[20].erase(iter);
}
}
}
else//是'c'
{
if(!c[20].empty())//能一步转'a'
{
a[i]=0;
c[20].erase(c[20].begin());
}
else if(!c[21].empty()&&!c[10].empty()
&&c[10].lower_bound(*c[21].begin())!=c[10].end())//不能一步转 -> "cb""ba"
{
auto iter=c[10].lower_bound(*c[21].begin());
a[i]=0;
c[21].erase(c[21].begin());
c[10].erase(iter);
}
else if(!c[21].empty())//不能转到'a' -> 只能转到'b'
{
a[i]=1;
c[21].erase(c[21].begin());
}
}
}
for(int i=0;i<n;i++)
{
cout<<char(a[i]+'a');
}
cout<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}啧,这个题自己补的时候思路其实对了,但就是没考虑到操作的顺序也会产生影响,错解里直接读相应操作出现的次数,然后就WA2了……
整体思路就是考虑所有操作出现的组合,三个字母无非就是“ab”“ac”“ba”“bc”“ca”“cb”这六种。而为了让字典序最小,所以就是从高位到低位依次考虑。来到每一位时,首先只要能变成“a”肯定变“a”,变不到的话再考虑“b”的情况。所以对于转成“a”而言,可以“ba”“ca”直接一步转,还可以经过“bc”"ca"和“cb”“ba”这两种情况两步转到“a”。那么之后的思路就是,如果当前位为“a”就直接不看去下一位。当不是“a”时,如果能一步直接转到“a”就直接转,不能的话再考虑两步转的操作。而对于两步转的操作,如果第一种情况“bc”"ca"有一种不存在就不能转,而第二种情况即使“ba”不存在,也可以通过“cb”将“c”转成“b”。
所以实现方法就是先把操作转成一个两位数,接着再把字符串也转成数方便计算。为了记录每种操作出现的位置,所以考虑用一个set存对应操作的那个两位数的所有出现位置。之后从高位到低位遍历字符串,是“a”就跳过,不是“a”的话才考虑。首先如果能一步转成就直接转,不能的话可以用一个lower_bound在第二步的所有操作位置的set里找大于等于第一步操作最早出现的位置。若此时迭代器不等于end说明有第二步操作,那就可以转,最后每次把第一步操作的begin和第二步操作的iter删除。这样就能保证不打乱操作顺序。
总结
思维还是不够,多想多练吧……