up:
溶金落梧桐
溶金落梧桐的个人空间-溶金落梧桐个人主页-哔哩哔哩视频
蓝桥杯三十天冲刺系列
BV18eQkY3EtP
网站:
OI Wiki
OI Wiki - OI Wiki
注意
比赛时,devc++勾选c++11(必看)
必须勾选c++11一共有两个方法,任用一个就可以了。(方法一有两个c++11可以选,好像都可以)
如果不勾选,map、to_string等不能使用,无法编译
蓝桥杯用的是c++11,所以C++17自带gcd函数或GCC拓展的__gcd函数不能用
- 方法一:

- 方法二

c++大概一秒跑10⁸的数据
10^8,大约是2^26次
对于子集枚举的算法中,O(n)=2^n
int大约2.1*10^9
long long大约9.2*10^18
c++除法 / 是向0取整(对于正数就是向下取整)
return退出函数
return 可以用来退出函数,如果是嵌套的循环,想要直接退出,要在每一层循环都break
可以用return
一般在main函数中调用solve()函数,在solve()函数中写解题逻辑
void solve(){
for(){
for(){
for(){
//这里使用return,直接退出了循环
//如果用break,在这里要使用三次,每一层都写一遍
return;
}
}
}
}
int main(){
solve();
return 0;
}变量int _=1;
首先使用
_作为变量名是符合语法规则的使用 _ 来作为这种控制循环次数的变量。一种竞赛时的默认写法,有一定的通用性
#include <bits/stdc++.h>
using namespace std;
void solve(){
}
int main() {
//使用下划线
int _=1;
while(_--)solve();
return 0;
}万能头
定义万能头,不需要敲所有的头文件了,因为都包含了
缺点:影响编译速度,和运行速度没有关系,所以比赛可以用
#include <bits/stdc++.h>关闭缓冲流
提高运行效率
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
return 0;
}endl比'\n'慢
直接这样换,即打的轻松,又用了'\n'
#define endl '\n'#define int long long
如果代码中混合使用 int 和 long long,可能导致隐式类型转换错误。统一使用 long long 可以避免这类问题
int main必须改为signed main
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main(){
return 0;
}数组开大一点点,定义到全局
对于题目给出的数组,自己定义的时候,开大一点点(数字随便,多10个甚至9个都行),为了防止数组越界
数组定义到全局里,不要定义在main中,c++中,如果把数组定义到main函数中,main函数是栈空间,空间比较小,一定义可能会把栈爆了
#include <bits/stdc++.h>
using namespace std;
//如果题目要求a数组最大是1000,开大一点点
//定义到全局,不要定义在main函数中
const int NN=1010;
int a[NN];
int main(){
return 0;
}记忆化搜索的dp,如果是多测(多组测试数据),不要写memset
memset的复杂度是数组的空间复杂度,如果是多组测试数据,用for循环手动把dp初始化成-1
main函数外声明的函数顺序影响调用
同理全部变量的声明也要放在最上面
#include <bits/stdc++.h>
using namespace std;
//可以在最上面使用函数声明({}前的,带个分号),这么就无关定义顺序了
void f2();
//这个f3不可以使用,因为f3之中有f2,f2还没有定义,f3不知道调用什么
void f3(){
f2();
}
void f2(){
}
//这个f1可以使用,因为f2已经定义了,f1在调用f2的时候知道是什么函数
void f1(){
f2();
}
int main() {
return 0;
}由数据范围反推算法复杂度以及算法内容
枚举

题目
蓝桥杯第15届-好数
日期模拟
得到星期:
在最外层的year循环外面,int week=x;//x是第一天的星期
在第三层day循环里面,week=week%7
题目
蓝桥杯 2024 省 A-艺术与篮球

#include <bits/stdc++.h>
using namespace std;
int ans=0;
int bh[]={13,1,2,3,5,4,4,2,2,2};
int months[]={-1,31,28,31,30,31,30,31,31,30,31,30,31};
bool leap(int year){
return (year%400==0)||((year%4==0)&&(year%100!=0));
}
void solve(){
for(int year=2000;year<=2024;year++){
//闰年特判
months[2] = leap(year) ? 29 : 28;
for(int month=1;month<=12;month++){
for(int day=1;day<=months[month];day++){
int y1,y2,y3,y4,m1,m2,d1,d2;
y1=year/1000;
y2=year/100%10;
y3=year/10%10;
y4=year%10;
m1=month/10%10;
m2=month%10;
d1=day/10%10;
d2=day%10;
int sum=bh[y1]+bh[y2]+bh[y3]+bh[y4]
+bh[m1]+bh[m2]
+bh[d1]+bh[d2];
if(sum>50)ans++;
if(year==2024&&month==4&&day==13)return;
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
cout<<ans;
return 0;
}进制转换

将字符转换成数字
如果是数字字符,这个字符 c - '0' 就能直接转换为对应的数字值
如果是字母字符,判断条件字符 c >= 'A',c - 'A' + 10 就能转换为对应的数字值(16进制,A表示10,所以字母对应数字是从10开始的)
提升位权(把字符变数字一定要提升位权)
之前累加的结果 ans 乘以进制 k,这相当于把之前的结果左移一位(也就是提升一位位权)
K进制转十进制

c是char类型,是字符。如字符'1'是按照ascii存,数字字符-'0'得到int类型的数字
int calc(char c) {
// 如果字符是字母(即大于 '9')转换为对应的数字值(A=10, B=11, ...)
if(c >= 'A') return c - 'A'+10;
// 如果是数字字符,直接转换为对应的数字值
return c - '0';
}
int change(int k, string s) {
int ans = 0;
for(int i = 0; i < s.size(); i++) {
ans = ans * k + calc(s[i]); // 基于进制 k 进行累加
}
return ans; // 返回转换后的十进制数
}十进制转K进制(短除法)
关键:十进制x%=k(得到k进制的当前位),然后x/=k(更新x)

string change(int x, int k) {
string ans; // 初始化空字符串,用于存储转换结果
while (x) {
int tmp = x % k; // 计算 x 对 k 取余,得到当前位的值
// 如果余数小于等于9,直接将其转换为字符并追加到结果字符串
// 因为是字符串和字符,所以+代表拼接
if (tmp <= 9) {
// '0' + tmp 转为对应数字字符的ASCII码
//因为tmp是int,'0'强转成int,所以得到得是ASCII码中的整数
//需要强转成char才能获得真正对应的数字字符
ans = ans + (char)(tmp + '0');
} else {
// 如果余数大于9,表示需要用字母 A, B, C...表示(例如10为A,11为B等)
// tmp - 10 + 'A' 转为对应字母字符的ASCII码
ans = ans + (char)( tmp - 10 + 'A' );
}
x /= k; // 更新 x,x 除以 k
}
// 将结果字符串反转并返回,返回的字符串为转换后的进制表示
reverse(ans.begin(), ans.end()); // reverse反转字符串(注意:没有返回值)
//返回反转的字符串
return ans;
}题目
穿越时空之门

#include <bits/stdc++.h>
using namespace std;
int cnt=0;
//求k进制各数位之和
int calc(int n,int k){
int sum=0;
while(n){
sum=sum+n%k;
n/=k;
}
return sum;
}
void solve(){
for(int i=1;i<=2024;i++){
if(calc(i,2)==calc(i,4))cnt++;
}
}
int main(){
solve();
cout<<cnt;
return 0;
}一维前缀和
一维前缀和,即一个数列中,某个数的前n项和=前n-1项的和+这个数
计算前缀和时,索引从1开始,让prefix[0]用默认的0
区间和查询
sum[ l,r ]区间和,即 l~r 之间的和,即 r 的前缀和减去 l 前面一项的前缀和
不会看,直接无脑把区间和sum设置成long long类型后,就不管了
在题目求和中,运用了一维前缀和的思维,出现了int*int的情况,强转成long long防止溢出
sum=sum+(long long)a[i]*(prefix[n]-prefix[i]);
前缀和求差分得到原数组
差分,就是后一项减去前一项的行为
a[ i ] = prefix[ i ] - prefix[ i-1 ] // 对于 i > 0

题目
一维前缀和
#include <bits/stdc++.h>
using namespace std;
const int NN=1e5+10;
int n,q;
int a[NN];
int prefix[NN];
int main() {
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>a[i];
prefix[i]=prefix[i-1]+a[i];
}
int sum=0;
for(int i=0;i<q;i++){
int l,r;
cin>>l>>r;
int sum=prefix[r]-prefix[l-1];
cout<<sum<<endl;
}
return 0;
}求和(强转成long long类型,防止溢出)

思路:
#include <bits/stdc++.h>
using namespace std;
const int NN=2e5+10;
int a[NN];
int b[NN];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=b[i-1]+a[i];
}
long long sum=0;
for(int i=1;i<n;i++){
//i=1时,是a2+a3+...+an,第一个元素索引是i+1,b[i+1-1]
//这里int*int会溢出,强转成long long
sum=sum+(long long)a[i]*(b[n]-b[i]);
}
cout<<sum;
return 0;
}一维差分(解决区间修改问题)
对差分数组求前缀和得到原数组(个人理解:求第i项原数组=前一项(i-1)原数组+位置i-1到i的变化率(diff[ i ]))
a[ i ] = a[ i-1 ] + diff[ i ]
a[i-1]:表示前一个位置(i-1)的原始值
diff[i]:表示从位置i-1到位置i的"变化量"或"增量"(即变化率)

差分数组,即这一项与前一项之差
对于数组[ 2,3,7,4,5,1 ],一维差分[ 2,1,4,-3,1,-4 ]
一维差分的前缀和就是原数组(可以看成积分求面积)
快速区间修改
在区间[ l,r ]修改
b[l] += d,相当于对后面所有的项都形成了“连坐”的反应,要求在[ l,r ]区间修改,即希望这个“连坐”只在这个区间有效,所以 b[r+1] -=d 来消除“连坐”影响(差分,就是变化率,对差分的修改,就是直接修改了变化率,而不是修改原数组)
对于数组[ 2,3,7,4,5,1 ],一维差分[ 2,1,4,-3,1,-4],希望[ 3,7,4 ]这个序列全部加上3,对应公式b[2]+=3,b[5]-=3
先看b[2]+=3,后面全部被影响了
再看b[5]-=3
判定序列中是否全部数字相同
已知:差分数组求前缀和就是原数组
当差分数组除第一项以外的所有项数均为0时,原数组一定所有数字相同(因为前缀和一致)
让某一项-1,再让某一项+1(相当于对原序列中的某一个连续的区间全部-1)
最后再让某一项-1
如:
1 2 -1
第二项-1,第三项+1:1 1 0
第二项-1,让不参与计算的n+1项+1: 1 0 0 [+1]
无解的情况
1 2 -3
无论如何 -3不能变成0,因为只能让某一项-1后,让某一项+1,第一项是不参与的,其他的正数和,比-3小,所以不够
在正数和<负数和时,无解
让原数组变成相同的数字
就是让一维差分数组的的b[1]有值,而且所有都是0
i==1时的特判
让一维差分方程b[i](i>1)变成0的操作数,就是所有一维差分数组中所有的正数的和
b[1] 作为差分数组的第一个元素,和其他 b[i](i > 1) 一样,都是差分数组整体的一部分。在处理差分数组时,为了保证处理逻辑的一致性和完整性,把b[1]的值也加上,先把它视做和其他b[i]一样要归0的数
因为本题要求原数组最后全为1,即要b[1]=1,所以在代表操作数的ans+b[1]只有-1,表示留下数字,不要操作,比如这里希望b[1]=1,就要-1,表示操作时,要留下一个数字不操作,它就被保留下来了,最后就是b[1]=1。如果是-1,表示留下两个数字不操作,最后就是b[1]=2
i==1时的特判,按情况而定
long long ans=0;
for(int i=1;i<=n;i++){
//i=1时的特判
if(i==1){
ans=ans+diff[1]-1;
}else{
if(b[i]>0)ans=ans+diff[i];
}
}题目
一维差分

#include <bits/stdc++.h>
using namespace std;
const int NN=2e5+10;
int n,m;
int a[NN],b[NN];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];
}
for(int i=1;i<=m;i++){
int l,r,d;
cin>>l>>r>>d;
b[l]+=d;
b[r+1]-=d;
}
for(int i=1;i<=n;i++){
b[i]=b[i-1]+b[i];
cout<<b[i]<<" ";
}
return 0;
}小蓝的操作数

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],diff[N];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
diff[i]=diff[i]-diff[i-1];
}
long long ans=0;
for(int i=1;i<=n;i++){
//i=1时的特判
if(i==1){
ans=ans+diff[1]-1;
}else{
if(b[i]>0)ans=ans+diff[i];
}
}
cout<<ans;
return 0;
}二维前缀和
二维前缀和
prefix是前缀和数组,a是原序列(即这个格子的值)
prefix[ i ][ j ] 表示从 a[ 1 ][ 1 ] 到 a[ i ][ j ] 的子矩阵中所有元素的和
构造二维前缀和数组公式:
prefix[ i ][ j ]=prefix[ i-1 ][ j ]+prefix[ i ][ j-1 ]-prefix[ i-1 ][ j-1 ]+a[ i ][ j ];
(s[ i ][ j ]=a[ i ][ j ]+s[ i-1 ][ j ]+s[ i ][ j-1 ]-s[ i-1 ][ j-1 ],两个是一样的,用prefix名字清晰,图中忽视S,只看坐标就行)
通过二维前缀和数组,求解某个子矩阵数组的值:
求解(x1,y1)到(x2,y2)
prefix[ x2 ][ y2 ]-prefix[ x1-1 ][ y2 ]-prefix[ x2 ][ y1-1 ]+prefix[ x1-1 ][ y1-1 ]
前缀和求差分得到原数组(差分,就是前一项减去后一项)
a[ i ][ j ] =prefix[ i ][ j ]-prefix[ i−1 ][ j ]-prefix[ i ][ j−1 ]+prefix[ i−1 ] [ j−1 ]
二维前缀和

#include <bits/stdc++.h>
using namespace std;
const int NN=1010;
int a[NN][NN],s[NN][NN];
int n,m,q;
int main(){
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
//构建二维前缀和数组
prefix[i][j]=prefix[i-1][j]+prefix[i][j-1]-prefix[i-1][j-1]+a[i][j];
}
}
for(int i=1;i<=q;i++){
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
cout<<prefix[x2][y2]-prefix[x1-1][y2]-prefix[x2][y1-1]+prefix[x1-1][y1-1]<<endl;
}
return 0;
}二维差分(子矩阵修改问题)

用差分数组进行区间更新:
假设我们要对子矩阵 (x1,y1) 到 (x2,y2) 的所有元素加上 d,可以转化为对差分数组 diff[][] 的 4 个单点操作
这个一个二维的差分
希望对(x1,y1)到(x2,y2)这一块就加上d,对diff[x1][y1]+d之后,从(x1,y1)开始,一直到最右下角(某个点(n,m))都会加上d
这时候,我们要消除不需要的加d操作
diff[ x1 ] [y1 ] += d(标记左上角,表示从 (x1,y1) 开始的所有区域都 +d,一直加到了右下角,)
diff[ x2+1 ][ y1 ] -= d(标记左下角,表示从 (x2+1,y1) 开始的所有区域撤销 +d)
diff[ x1 ] [ y2+1 ] -= d(标记右上角,表示从 (x1,y2+1) 开始的所有区域撤销 +d)
diff[ x2+1 ][ y2+1 ] += d(右下角,多减的补回来)
二维差分求前缀和,得到原数组(原数组=前一项数组+变化率diff):
a[ i ][ j ]=a[ i−1 ][ j ]+a[ i ][ j−1 ]−a[ i−1 ][ j−1 ]+diff[ i ][ j ]
构造差分数组(后一项减前一项):
diff[ i ][ j ]=a[ i ][ j ]-a[ i−1 ][ j ]-a[ i ][ j−1 ]+a[ i−1 ][ j−1 ]
(对于差分的理解就是前一项减去后一项,但是在二维数组中,二维的“后一项”是从左上角到这个点( i,j )的,而“前一项”也是同理,对于二维,要减去这个点( i,j )的左侧( i,j-1 )和上侧(i-1,j),再补上多减的( i-1,j-1 ))
题目
二维差分

#include <bits/stdc++.h>
using namespace std;
const int NN=1010;
int a[NN][NN];
int diff[NN][NN];
int n,m,q;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>q;
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
cin>>a[i][j];
diff[ i ][ j ]=a[ i ][ j ]-a[ i-1 ][ j ]-a[ i ][ j-1 ]+a[ i-1 ][ j-1 ];
}
}
//查询
while(q--) {
int x1,y1,x2,y2,d;
cin>>x1>>y1>>x2>>y2>>d;
diff[x1][y1]+=d;
diff[ x2+1 ][ y1 ] -= d;
diff[ x1 ] [y2+1 ] -= d;
diff[ x2+1 ][ y2+1 ] += d;
}
//求前缀和
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = diff[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
cout << a[i][j] << " ";
}
cout << endl;
}
return 0;
}棋盘

#include <bits/stdc++.h>
using namespace std;
const int NN=2010;
int a[NN][NN],diff[NN][NN];
int n,m;
int main()
{
cin>>n>>m;
while(m--){
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
//原数组是0,差分数组也是0,不用在构建差分数组了,直接操作
diff[x1][y1]+=1;
diff[x2+1][y1]-=1;
diff[x1][y2+1]-=1;
diff[x2+1][y2+1]+=1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+diff[i][j];
//反转奇数次就是1,反转偶数次就是0
cout<<a[i][j]%2;
}
cout<<endl;
}
return 0;
}二分
左程云-二分搜索
BV1bX4y177uT
序列二分
"大于等于"和"等于的最左边"(即查找第一个满足条件的元素,即求最小,舍弃右边)可以使用同一个模板
"小于等于"和"等于的最右边"(即查找最后一个满足条件的元素,即求最大,舍弃左边)可以使用同一个模板
输出有序数组中等于 x 的最左边的数的下标
因为求的是最左边的x,所以把右边抛弃,a[mid] 在 x 右边,包含了mid这个位置(a[mid]>=x),右边不要(r=mid)(因为包含了mid这个位置,即a[mid]有等于x的可能,不能把mid这个位置舍去)
a[mid] 在 x 左边的可能,不包含mid这个位置(a[mid]<x),左边不要(l=mid+1)(因为不包括mid这个位置,a[mid]不等于x,
它一定不是要求的位置,把包含mid的左边部分舍去,由于舍弃的是左边,即要加1,在更右边的位置从算把mid一起舍弃)
while(l < r) {
int mid = l + r >> 1;
if(a[mid] >= x) r = mid;
else l = mid + 1;
}
if(a[l] == x) cout << l << endl;输出有序数组中等于 x 的最右边的数的下标(求最大,把左边抛弃)
思路和前面一样
只是把包含mid的右边部分舍去,由于舍弃的是右边,即要减1,在更左边的位置才算把mid一起舍弃
int mid=l+r+1>>1,记住和 mid-1 绑定
while(l < r) {
int mid = l + r + 1 >> 1;
if(a[mid] <= x) l = mid;
else r = mid - 1;
}
if(a[l] == x) cout << l << endl;查找第一个大于x的元素(不含等于)
对于a[mid]==x的情况
在大于等于x,和小于等于x的要求中,要把a[mid]保留
但在大于x或者小于x的要求中,要把a[mid]跳过
while(l < r) {
int mid = l + r >> 1;
if(a[mid] > x) { // 仅大于,不含等于
r = mid;
} else {
l = mid + 1; // 包括等于的情况都跳过
}
}查找最后一个小于x的元素(不含等于)
while(l < r) {
int mid = l + r + 1 >> 1;
if(a[mid] < x) { // 仅小于,不含等于
l = mid;
} else {
r = mid - 1; // 包括等于的情况都跳过
}
}upper_bound()和low_bound()函数
upper_bound()和lower_bound(),stl中的二分查找函数,返回的是一个指针/迭代器
upper_bound(first,last,value):
在范围 [first,last) 内查找第一个大于value的元素位置(结果减1得到了最后一个小于等于value的位置,注意题目)lower_bound(first,last,value):
在范围 [first,last) 内查找第一个不小于(大于等于)value的元素位置(用value+1来达成和upper_bound一样,找到大于value的元素)
对于引用:比如&a[3],想要获得引用的值,只需要让引用减去第0项的引用,在这里就是&a[3]-&a[0]
对于数组,如int a[N],a本身就是第0项的引用,所以也可以写成&a[3]-a,让得到的是元素在数组中的索引(从0开始)
题目
整数查找(模板题)
蓝桥账户中心
最大通过数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
ll a[N],b[N];
int main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,m,k;
cin>>n>>m>>k;
for(int i=1; i<=n; i++) {
cin>>a[i];
//原地做前缀和
a[i]=a[i-1]+a[i];
}
for(int i=1; i<=m; i++) {
cin>>b[i];
//原地做前缀和
b[i]=b[i-1]+b[i];
}
int ans=0;
//因为关卡或许连第一关都没过,所以索引从0开始
for(int i=0; i<=n; i++) {
//第一关水晶用完了,break
if(a[i]>k)break;
//第一关剩下的水晶
ll rest=k-a[i];
//upper_bound找到首个大于value的元素的迭代器,得到结果-1,获得最后一个小于等于value的迭代器,减去数组得到元素值
//b+m+1,+1确保搜索到最后一个元素,因为upper_bound和lower_bound都是[first,last)
int j=upper_bound(b,b+m+1,rest)-1-b;
ans=max(i+j,ans);
}
cout<<ans;
return 0;
}暴力
答案二分

左程云
BV1Mh4y1P7qE

阶乘后的0(额外)
阶乘尾数的0,是由1到n中,因子10的数量决定,每有一个10,新增一个0
而10=2*5
含有2的因子,每两个出现一次,含有5的因子,每五个出现一次
所以因子5的个数一定小于因子2的个数
所以求1到n中因子5的个数就是答案
含有5的因子,每五次出现一次(5,10,15……)
含有5的平方的因子,每25(5的平方)次,出现一次(25,50……)
含有5的三次方的因子,每125(5^3)次,出现一次(125……)
依此类推
int countTrailingZeros(int n) { int cnt = 0; while (n) { cnt += n/5; //除以5,方便进行迭代 n /= 5; } return cnt; }
题目
二分答案
解析
随着枚举的最小值变大,消耗的x越来越多,即x剩余的越来越少
对于枚举的 i,上限在本题中是10^6+10^13(操作数k+a的最大值),这里直接用1e14

进行二分,对中间的m进行左边的操作,如果不对,就不要了
然后就是普通二分的思路了

代码
暴力(过不了,了解一下思路)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int NN=1e5+10;
ll k;
int n;
int a[NN];
void solve(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
}
//用来枚举数组中最小值,即通过最多k次操作使得数组中的所有元素都至少为i
/*输入的a上限是1e6,操作次数k上限是1e13,当序列中只有一个数是1e6
k次操作后这个数最大的可能性是这个数最大可能性变成1e13+1e6*/
for(int i=1;i<=1e13+1e6;i++){
/*用ll cnt=0 //cnt表示操作数*/
//把操作数赋值给x
ll x=k;
//用来枚举序列中每一个数
for(int j=1;j<=n;j++){
//如果这个数小于最小值,更新操作数
if(a[j]<i){
k=k-(i-a[j]);
/*cnt+=i-a[j] //把每次需要的操作数加上,也可以这样想,不过对于答案二分的「给定条件」和「问题答案」之间的关系不明确*/;
}
//至少要把数组中每一个变成i,操作次数不够,就不能把每一个数变成i了
//i-1 是最后一个满足条件的 i(因为 i-1 时 k 还没耗尽)
/*if(cnt>k)*/
if(x<0){
cout<<i-1;
return;
}
}
}
}
int main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
while(t--){
solve();
}
return 0;
}答案二分
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int NN=1e5+10;
ll k;
int n;
int a[NN];
bool check(ll m){
ll x=k;
for(int j=1;j<=n;j++){
if(a[j]<m){
//得到剩余操作数
x=x-(m-a[j]);
}
if(x<0){
return false;
}
}
return true;
}
void solve(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
}
//r表示上限,应该是a的最大值+k的最大值,1e6+1e13,这里用1e14方便写
ll l=1,r=1e14;
while(l<r){
ll mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
cout<<l;
}
int main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
while(t--){
solve();
}
return 0;
}代码解析
贪心思想:
对于每个元素,严格按需分配操作次数:只提升不足m的部分。
不浪费操作次数在已经≥m的元素上
(m - a[ j ]) 的含义:
如果当前元素 a[ j ] 小于 m,则需要将它从 a[ j ] 提升到 m。需要操作的次数 = 两者的差值 = m - a[ j ]
(例如:a[ j ]=2,m=5 → 需要 5-2=3 次操作)
if(check(mid)) l=mid:
这里true的情况是所有元素>=mid的情况,所以包含了mid
求阶乘

代码(90%)
#include <bits/stdc++.h>
using namespace std;
#define int long long
int countZero(int n) {
int cnt = 0;
while (n){
cnt += n / 5;
n /= 5;
}
return cnt;
}
int K;
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> K;
int l = 0, r = 1e18;
while (l < r) {
int mid = l + r >> 1;
if (countZero(mid) >= K) r = mid;
else l = mid + 1;
}
if (countZero(l) == K) cout << l;
else cout << -1;
return 0;
}数列分段

题目解析
数组4 2 4 5 1,要求分成三段
我们假设,每一段的最大值是1
放入第一个数组4,就直接爆了,不行
依次类推,枚举的最大值,从1开始到3,都会爆
直接看5
数组4 2 4 5 1,放了三个数字,5放不进,所以枚举的最大值5不行
枚举每一段的最大值是6
首先放入4,发现可以放后面的数字2,就继续放,第一段放了4和2
之后数组都能放进去
所以6是最先符合的
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int NN=1e5+10;
int a[NN];
int N,M;
bool check(ll mid){
//每一段内的和,用来判断分段
ll sum=0;
//段数,一开始默认段数就是1了
int cnt=1;
for(int i=1;i<=N;i++){
//这个数大于要求的最大值,怎么也放不进,直接false
if(a[i]>mid)return false;
if(sum+a[i]<=mid){
sum+=a[i];
}else{
//当这一段爆了之后,增加一段,里面的容量重新开始算
cnt++;
sum=a[i];
}
}
return cnt<=M;
}
void solve(){
cin>>N>>M;
for(int i=1;i<=N;i++){
cin>>a[i];
}
ll l=1,r=(ll)(1e13);
while(l<r){
ll mid=r+l>>1;
if(check(mid))r=mid;
else l=mid+1;
}
cout<<l;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t=1;
while(t--)solve();
return 0;
}代码解析
当枚举的最小值的二分后,mid所代表的cnt>m了,所以mid不行,二分逻辑上的mid的左边舍去
当枚举的最小值的二分后,mid所代表的cnt<m了,这里代表因为枚举出来的要求的最小值偏大了,所以实际的段数更少
如:一共五个数:4 2 2 5 1,要求分成三段
枚举的8作为最小值偏大了,所以用两段就足够了,但实际上,把枚举的最大值缩小,前两段中也有数字能放进第三段
所以check检查的逻辑是:段数cnt<=m
因为比要求的段数m更少的段数cnt也可以,只是没有达到二分上mid最好的值
浮点数二分
up说不大可能会考,所以没看
高精度加法
栈

指针一开始指向栈的第一格的下面

题目
模拟栈

#include <bits/stdc++.h>
using namespace std;
const int NN = 1e5 + 10;
int stk[NN];
int top = -1;
void push(int x) {
stk[++top]=x;
}
void pop() {
top--;
}
bool empty() {
return top==-1;
}
int query() {
return stk[top];
}
void solve() {
int m;
cin >> m;
while (m--) {
string op;
cin>>op;
if (op=="push") {
int x;
cin>>x;
push(x);
} else if (op=="empty") {
if(empty())cout<<"YES\n";
else cout<<"NO\n";
} else if (op == "pop") {
if (!empty()) pop();
} else{
if (empty()) cout<<"empty\n";
else cout<<query()<<"\n";
}
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t = 1;
while (t--) solve();
return 0;
}递归
对于递归,只需模拟最后两层,剩下所有的递归和最后两层是一样的
回溯
dfs一种是正常的回溯法,一种是在图上进行的dfs操作
子集枚举(递归实现指数型枚举,O(n)=2^n)
对于每个东西,是选和不选,删和不删,留和不留
一旦涉及到两个状态,就是子集枚举

对角线(额外)
主对角线(正对角线):n - j + i(主对角线是从方阵的左上角延伸到右下角的一条线,该线上每个元素的行索引和列索引相等,即i=j)
方向:从 左上到右下(↘️)数学性质:同一主对角线上的所有点满足 行号 - 列号 = 常数(即 i - j = C)
例如:点 (3,1) 和 (4,2) 在同一条主对角线上,因为 3-1 = 4-2 = 2
索引处理:
原始公式 i - j 可能为负数(如 i=1, j=2 → 1-2=-1)
通过变形 n - j + i 确保索引为正数
辅对角线(反对角线):i + j(在二维数组中,对于一个n*n的方阵,若以 0 开始计数,辅对角线元素的行索引 i 和列索引 j 满足i + j = n - 1)
方向:从 右上到左下(↙️)
数学性质:同一副对角线上的所有点满足 行号 + 列号 = 常数(即 i + j = C)
例如:棋盘上的点 (2,3) 和 (1,4) 在同一条副对角线上,因为 2+3 = 1+4 = 5
对角线的数量是2*N-1(对角线是所有斜着的线,不光是中间的那根)
题目
递归实现排列型枚举

#include <iostream>
using namespace std;
const int NN=10;
int path[NN];
bool vis[NN];
int n;
void dfs(int u){
//出递归
if(u>n){
for(int i=1;i<=n;i++){
cout<<path[i]<<" ";
}
cout<<"\n";
return;
}
//
for(int i=1;i<=n;i++){
if(!vis[i]){
vis[i]=1;
//path用来记录已经确定的排列顺序
path[u]=i;
//下一层
dfs(u+1);
//回溯
vis[i]=0;
}
}
}
int main()
{
cin>>n;
dfs(1);
return 0;
}N皇后
N*N的方格放置N个皇后
即要求每一行都放置一个皇后

#include <bits/stdc++.h>
using namespace std;
const int NN=20;
//fan反对角线,zhu主对角线
bool col[NN],zhu[NN],fu[NN];
int N;
int cnt=0;
//i表示当前正在处理的行号,看每一行是否有位置
void dfs(int i) {
//可以填棋子,如果能填完最后一行,就是一个可行解
//代表当前行号的u大于要求的行数n,因为i==n时,最后一行还没有开始填
if(i>N) {
cnt++;
return;
}
for(int j=1; j<=N; j++) {
if(!col[j]&&!zhu[N-j+i]&&!fu[i+j]) {
//dfs()中的数是按行枚举,如果这个位置有了,它所在的列、主对角线、反对角线不能有棋子
//在这个位置有棋子时,可以标记所在的列、主对角线、反对角线为访问过,下次不能访问
col[j]=1;
zhu[N-j+i]=1;
fu[i+j]=1;
//访问下一个
dfs(i+1);
//回溯
col[j]=0;
zhu[N-j+i]=0;
fu[i+j]=0;
}
}
}
void solve() {
cin>>N;
dfs(1);
cout<<cnt;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t=1;
while(t--)solve();
return 0;
}递归实现指数型枚举(n<=25都可以用)
题目解析
x代表不选,数字代表选了,?代表正在选

代码
#include<bits/stdc++.h>
using namespace std;
const int N = 16;
int n;
//status,表示选或不选的状态
bool st[N];
//u是当前正在处理的数字
void dfs(int u) {
//当u>n时,所有数字遍历完,遍历st数组,打印所有st[i]=1的数字
if(u>n) {
for(int i=1;i<=n;i++) {
if(st[i]) cout<<i<<" ";
}
cout<<endl;
return;
}
//选和不选在这里就是一种回溯,改变顺序会有影响,这里是先不选后选的情况
//不选u
st[u]=0;
//处理下一个数字
dfs(u+1);
//选u
st[u]=1;
//处理下一个数字
dfs(u+1);
}
int main() {
cin >> n;
dfs(1);
return 0;
}二进制枚举(O(n)=n*2^n)

基本位运算:
左移<<:二进制位中,在右边补0
这里1<<3,在二进制中补三个0,就是1000,就是8
对于一个十进制数:
<<1,就是*2
>>1,就是/2
&1,就是保留二进制位最后一位的值
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n; // 输入集合的大小 n
// 遍历所有可能的子集(2^n 种)
for (int i = 0; i < (1 << n); i++) {
// 检查每个元素是否被选中
for (int j = 0; j < n; j++) {
if ((i >> j & 1) == 1) { // 如果 i 的第 j 位为 1
// 这里可以处理选中的元素
// 例如:输出选中的元素
cout << j << " ";
}
}
cout << "\n"; // 换行,表示一个子集结束
}
return 0;
}行==0或列==0或对角线==0,五子棋也没有获胜(额外)
当 row 或者 col 的值等于 0 时,这表明当前行或者当前列上没有放置任何一方的棋子,或者全部放置的是另一方的棋子
在代码逻辑里,同样把这种情况视为一方获胜(因为另一方没有在这一行或列落子),所以也判定当前棋盘状态不是平局对于主对角线和辅对角线也同理
题目
五子棋对弈

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
int a[30];//用一维数组从棋子落子情况,存放棋子是1还是0
int b[10][10];//用二维数组存棋盘
int ans=0;
bool check(){
int pos=0;
for(int i=0;i<5;i++){
for(int j=0;j<5;j++){
//把棋子落子情况从一维转成二维
b[i][j]=a[pos++];
}
}
//行和列棋子的情况
for(int i=0;i<5;i++){
int row=0,col=0;
for(int j=0;j<5;j++){
row+=b[i][j];//从左向右加,就是行
col+=b[j][i];//从上向下加,就是列
}
//行或列连成5颗棋子,不是平局
if(row==0||row==5||col==0||col==5)return false;
}
//对角线棋子的情况
int zhu=0,fu=0;
for(int i=0;i<5;i++){
//主对角线i=j
zhu+=b[i][i];
//辅对角线i+j=n-1
fu+=b[i][4-i];
}
//对角线连成5颗棋子,不是平局
if(zhu==0||zhu==5||fu==0||fu==5)return false;
return true;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n=25;
//遍历所有子集
for(int i=0;i<(1<<n);i++){
int cnt=0;
//检查每个元素
for(int j=n-1;j>=0;j--){
if((i>>j&1)==1)cnt++;
//用数组存棋盘中落子情况,表示棋盘第j位的棋子是1还是0
a[j]=(i>>j&1);
}
//一个25格,下满棋盘,所以白子13个,黑子12个
if(cnt!=13)continue;
if(check())ans++;
}
cout<<ans;
return 0;
}dfs和bfs题目
acwing,课程中的kuangbin
登录 - AcWing
bfs格式
bfs使用队列维护数据
在 BFS(广度优先搜索)中,使用队列(Queue)来维护待处理的节点,是因为 BFS 的核心思想是 按层级逐步扩展搜索,而队列的 先进先出(FIFO) 特性正好符合这一需求
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
//最大常量
const int NN=;
//对于图的搜索,可能需要地图
char g[NN][NN][NN];
//访问数组,如果题目状态唯一,没有重复和无意义的搜索路径,不需要访问数组
bool vis[NN][NN][NN];
//答案数组,如果题目结果唯一,不存在多个有效答案需要记录,不需要答案数组
int ans[NN][NN][NN];
struct point{
int x,y,z;
};
//使用队列,看情况使用结构体
queue<point> que;
//对于位置方向的移动,一般使用偏移量,看情况可能是一维、二维、三维
//{}中写出偏移量
//在某些题目不写偏移量
int dx[]={};
int dy[]={};
int dz[]={}
int bfs(){
while(!que.empty()){
//得到队列首元素
auto p=que.front();
//队头扩展搜索完毕后出队,避免重复搜索
que.pop();
//一维位置移动问题
//当当前位置x等于目标位置k时,就找到了最短路径,直接返回
//if(p==k)return ans[p];
//循环,进行遍历
for(){
//这个点的位置再加上偏移量就是下个点的位置
//nx的n表示next
int nx=p.x+dx[i], ny=p.y+dy[i], nz=p.z+dz[i];
//对边界的判断
if(){
//状态更新
vis[nx][ny][nz]=1;
//答案更新,下一个的位置就是上一个+1
ans[nx][ny][nz]=ans[p.x][p.y][p.z]+1;
//三维迷宫问题
//return语句处于if判断之中。因为一旦找到了目标位置,就意味着找到了最短路径,直接返回
if() return ans[nx][ny][nz];
//没有得到答案就入队
que.push({nx,ny,nz});
}
}
}
//如果0也是可能的答案,就return -1;
return 0;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
while(){
// 初始化(多个样例)
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
queue<point> empty; swap(que, empty);
// 读入
for(int i=1;i<=L;i++){
for(int j=1;j<=R;j++){
for(int k=1;k<=C;k++){
//读入地图
cin>>g[i][j][k];
if(g[i][j][k]=='S'){
//放入起点
que.push({i,j,k});vis[i][j][k]=1;
}
}
}
}
//答案
cout<<bfs();
}
return 0;
}坐标系
二维网格坐标系
和数学的笛卡尔坐标系不同,X向下,Y向右
在三维坐标系中,通常采用 右手坐标系(X向右,Y向前,Z向上)
// 右、左、前、后、上、下 int dx[] = {1, -1, 0, 0, 0, 0}; int dy[] = {0, 0, 1, -1, 0, 0}; int dz[] = {0, 0, 0, 0, 1, -1};
棋盘问题(dfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN=20;
int n,k,ans=0;
char g[NN][NN];//表示棋盘
bool col[NN];//代表每一行的每一列是否有棋子
//u:行,sum:总棋子数
void dfs(int u,int sum){
//符合条件得到答案,退出
if(sum==k){
ans++;
return;
}
//超出边界,退出
//先得到答案,再退出,如果先判断超出边界,无论sum 是否等于 k,都会直接返回
if(u>n)return;
//遍历每一列
for(int i=1;i<=n;i++){
if(!col[i]&&g[u][i]=='#'){
col[i]=1;
dfs(u+1,sum+1);
col[i]=0;
}
}
//这一行不能放棋子(没有#的情况),直接去下一行
dfs(u+1,sum);
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
while(cin>>n>>k,n!=-1&&k!=-1){
//每一次输入都要初始化访问数组和答案
memset(col,0,sizeof(col));
ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>g[i][j];
}
}
dfs(1,0);//枚举每一行
cout<<ans<<endl;
}
return 0;
}地牢大师(三维迷宫bfs)


#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN=110;
char g[NN][NN][NN];
int ans[NN][NN][NN];
bool vis[NN][NN][NN];
int L,R,C;
struct point{
int x,y,z;
};
queue<point>que;
int dx[]={1,-1,0,0,0,0};
int dy[]={0,0,1,-1,0,0};
int dz[]={0,0,0,0,1,-1};
//看情况bfs类型是int还是void
int bfs(){
while(!que.empty()){
auto p=que.front();
que.pop();
for(int i=0;i<6;i++){
int nx=p.x+dx[i],ny=p.y+dy[i],nz=p.z+dz[i];
if(nx>=1&&nx<=L
&&ny>=1&&ny<=R
&&nz>=1&&nz<=C
&&!vis[nx][ny][nz]
&&g[nx][ny][nz]!='#'){
vis[nx][ny][nz]=1;
ans[nx][ny][nz]=ans[p.x][p.y][p.z]+1;
if(g[nx][ny][nz]=='E')return ans[nx][ny][nz];
que.push({nx,ny,nz});
}
}
}
return 0;
}
int main(){
while(cin>>L>>R>>C,L!=0&&R!=0&&C!=0){
//初始化
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
queue<point>empty;
swap(que,empty);
//读入
for(int i=1;i<=L;i++){
for(int j=1;j<=R;j++){
for(int k=1;k<=C;k++){
cin>>g[i][j][k];
if(g[i][j][k]=='S'){
vis[i][j][k]=1;
que.push({i,j,k});
}
}
}
}
int res=bfs();
if(res)printf("Escaped in %d minute(s).\n",res);
else cout<<"Trapped!"<<endl;
}
return 0;
}抓住那头牛(一维位置移动bfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
//N,K上限是1e5,但是X有2*X的情况,所以X上限是2*1e5
const int NN=2e5+10;
int ans[NN];
bool vis[NN];
int N,K;
queue<int>que;
int dx[]={-1,1,2};
int bfs(){
while(!que.empty()){
auto x=que.front();
que.pop();
//当前位置 x 等于目标位置 K 时,就找到了最短路径,直接返回对应的步数 ans[x]
if(x==K)return ans[x];
for(int i=0;i<3;i++){
int nx;
if(dx[i]==2)nx=x*dx[i];
else nx=x+dx[i];
//边界判断
if(nx>=0&&nx<NN&&!vis[nx]){
vis[nx]=1;
ans[nx]=ans[x]+1;
que.push(nx);
}
}
}
return -1;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>N>>K;
vis[N]=1;
que.push(N);
cout<<bfs();
return 0;
}找倍数(状态唯一,没有访问数组,结果唯一,没有答案数组bfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
int n;
queue<int>que;
int bfs(){
while(!que.empty()){
auto p=que.front();que.pop();
if(p%n==0)return p;
//*10,相当于在末尾补0
que.push(p*10);
//*10+1,相当于在末尾补1
que.push(p*10+1);
}
return -1;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
while(cin>>n,n!=0){
queue<int>empty;
swap(que,empty);
//不考虑前导0,直接将1放入队列
que.push(1);
cout<<bfs()<<endl;
}
return 0;
}质数路径(位权)

#include <bits/stdc++.h>
using namespace std;
const int N = 10010; // 四位数的最大范围是9999,多一点,避免数组越界
int ans[N]; // 记录操作数
bool vis[N]; // 访问标记
int a[4]; // 存放数字的各位
int d[4] = {1000, 100, 10, 1}; // 位权偏移量
queue<int> que;
int A, B;
// 判断一个数是否为素数
bool isPrime(int num) {
if (num < 2) return false;
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
}
int bfs() {
while (!que.empty()) {
int p = que.front();que.pop();
if (p == B) return ans[p];
// 分解数字各位
//每次迭代结束时,先执行 i/=10,再执行 j--(如果颠倒不行)
//当 i 变为 0 时,循环立即终止,不会执行多余的 j--
//防止j变成负数,数据越界
for (int i = p, j = 3; i > 0; i /= 10,j--) {
a[j] = i % 10;
}
// 尝试修改每一位
for (int j = 0; j < 4; j++) {//遍历给出数字的每一位
for (int i = 0; i < 10; i++) {//对于每一位 j,这尝试将该位数字修改为 0 ~9 中的任意一个值
//优化
if (j == 0 && i == 0) continue; // 千位不能为0
//计算将数字 p 的第 j 位修改为 i 后得到的新数字 nx。
//其中 d[j] 是位权偏移量数组 d 中对应第 j 位的位权(如千位是 1000,百位是 100 等)
//a[j] 是数字 p 当前第 j 位的原始数字。
int nx = p + d[j] * (i - a[j]);
if (nx >= 1000 && nx < N && isPrime(nx) && !vis[nx]) {
vis[nx] = 1;
ans[nx] = ans[p] + 1;
que.push(nx);
}
}
}
}
return -1; // 如果无法到达
}
int main() {
int T;
cin >> T;
while (T--) {
cin >> A >> B;
//初始化
memset(ans, 0, sizeof(ans));
memset(vis, 0, sizeof(vis));
queue<int>empty;swap(que,empty);
//放入起点
que.push(A);
vis[A] = 1;
int res = bfs();
if (res != -1) {
cout << res << endl;
} else {
cout << "Impossible" << endl;
}
}
return 0;
}代码解析(新整数=原整数+对应位权*对应数位变化量)
(i - a[j]) 计算的是将整数 p 的第 j 位从 a[j] 修改为 i 时,该位数字的变化量
例如,如果 a[j] = 3,i = 5,那么 (i - a[j]) = 5 - 3 = 2,表示该位数字需要增加 2
d[j] * (i - a[j]) 则是将该位数字的变化量乘以对应的位权,得到由于这一位数字变化对整个整数的影响值。例如,对于百位(d[1] = 100),如果数字变化量是 2,那么 d[1] * (i - a[1]) = 100 * 2 = 200,表示百位数字变化 2 会使整个整数变化 200
p + d[j] * (i - a[j]) 就是在原整数 p 的基础上,加上由于第 j 位数字变化对整个整数的影响值,从而得到修改后的新整数 nx
罐子(把操作看成二维坐标)
把两个罐子倒水的操作看成二维坐标

题目

#include <bits/stdc++.h>
using namespace std;
struct Point {
// 当前两个容器的水量
int x, y;
// 操作步骤记录
//定义成string类型,将多个操作编号按顺序拼接起来
string steps;
};
const int NN = 110;
string op[6] = {
"FILL(1)", "FILL(2)", "DROP(1)",
"DROP(2)", "POUR(1,2)", "POUR(2,1)"
};
int ans[NN][NN]; // 记录到达每个状态的最少步数
bool vis[NN][NN]; // 标记状态是否被访问过
queue<Point> que;
int a, b, c; // 容器容量和目标水量
int bfs() {
while (!que.empty()) {
auto p = que.front();que.pop();
// 检查是否达到目标
if (p.x == c || p.y == c) {
cout << ans[p.x][p.y] << endl;
//在结构体中,每一个操作都拼接成了一个字符串,用增强for获得每一个操作,变成数字
for (char i : p.steps) {
cout << op[i - '0'] << endl;
}
return 0;
}
// 计算6种操作的水量变化
//pour1 表示从罐子 x(容量为 a)向罐子 y(容量为 b)倒水时,能够倒过去的水量
//取 p.x(罐子 x 当前的水量)和 b - p.y(罐子 y 还能容纳的水量)中的较小值
int pour1 = min(p.x, b - p.y); // POUR(1,2)
int pour2 = min(a - p.x, p.y); // POUR(2,1)
//两个罐子的变化量,六个操作对应六个值
int dx[] = {a - p.x, 0, -p.x, 0, -pour1, pour2};
int dy[] = {0, b - p.y, 0, -p.y, pour1, -pour2};
for (int i = 0; i < 6; i++) {
int nx = p.x + dx[i];
int ny = p.y + dy[i];
// 检查新状态是否合法且未访问
if (nx >= 0 && nx <= a && ny >= 0 && ny <= b &&!vis[nx][ny]) {
vis[nx][ny] = 1;
ans[nx][ny] = ans[p.x][p.y] + 1;
//结构体中定义了操作步骤是string,用+可以拼接
que.push({nx, ny, p.steps + to_string(i)});
}
}
}
return -1;
}
int main() {
cin >> a >> b >> c;
memset(ans, 0, sizeof ans);
memset(vis, 0, sizeof vis);
//放入起点,一开始两个罐子都是空的,且没有操作
que.push({0, 0, ""});
vis[0][0] = 1;
int res=bfs();
if(res==-1)cout<<"impossible"<<endl;
return 0;
}全球变暖(两个bfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN = 1010;
char g[NN][NN];
bool vis[NN][NN];
struct Point {
int x, y;
};
queue<Point> que; // 全局队列
int dx[] = {-1, 0, 1, 0};
int dy[] = {0, 1, 0, -1};
int N, sum=0, notYanMo=0;
// 判断岛屿是否会被完全淹没
bool willBeFlooded(int x, int y) {
queue<Point> empty;swap(que, empty);// 清空队列
que.push({x, y});
vis[x][y] = 1;
bool isFlooded = true; // 初始假设会被淹没
while (!que.empty()) {
auto p = que.front();que.pop();
//必须在 while 循环内部,确保每次处理新的陆地节点时,都能正确判断其是否有邻接海洋
bool hasAdjacentSea = false; // 当前陆地是否有邻接海洋
for (int i = 0; i < 4; i++) {
int nx = p.x + dx[i];
int ny = p.y + dy[i];
if (nx >= 1 && nx <= N && ny >= 1 && ny <= N) {
if (g[nx][ny] == '.') {
hasAdjacentSea = true; // 当前陆地有邻接海洋
} else if (g[nx][ny] == '#' &&!vis[nx][ny]) {
que.push({nx, ny});
vis[nx][ny] = 1;
}
}
}
// 如果当前陆地没有邻接海洋,整个岛屿不会被完全淹没
if (!hasAdjacentSea) {
isFlooded = false;
}
}
return isFlooded;
}
void bfs() {
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (g[i][j] == '#' &&!vis[i][j]) {
//因为willBeFlooded函数对每个陆地都bfs了
//所以bfs函数中的!vis[i][j] 保证了这个位置没有被其他 BFS 过程访问过
//所以当进入这个分支时,意味着发现了一个新的、独立的岛屿
sum++;//连通岛总数
if (!willBeFlooded(i, j)) {
notYanMo++;
}
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cin >> g[i][j];
}
}
bfs();
cout << sum - notYanMo << endl;
return 0;
}代码解析(isFlooded和hasAdjacentSea的bool值)

组合数

不选第n个数,在n-1个数中选m个数,就是n个数中选m个数的部分方案数
选第n个数,在n-1个数中,选择m-1个数,把这第n个数一加,就是n个数中选m个数的部分方案数
题目
递归求组合数

#include <iostream>
using namespace std;
int n,m,t;
int f(int m,int n){
if(n==m||m==0)return 1;
return f(m-1,n-1)+f(m,n-1);
}
void solve(){
cin>>n>>m;
int ans=0;
ans=f(m,n);
cout<<ans<<"\n";
}
int main()
{
cin>>t;
while(t--)solve();
return 0;
}记忆化搜索
数组的维度通常与问题的状态空间一致:
与dfs函数的参数一致
实现搜索函数:
检查当前状态是否已经被计算过
这一步要在递归边界下面写
一般写dfs函数,返回值是void,使用记忆化搜索,dfs的返回值写成int

#include <bits/stdc++.h>
using namespace std;
//1.定义记忆化数组
//记忆化数组的维度和问题的状态空间一致
//因为问题是求斐波那契数列,只有一个参数,所以一维
int dp[50];
int f(int n){
//递归边界
if(n==1||n==2)return 1;
//3.实现搜索函数,检查当前状状态是否被计算过
//这一步放在递归边界下
if(dp[n]!=-1)return dp[n];
//3.实现搜索函数,保存记忆化数组
//本来return f(n-1)+f(n-2);
//增加一个dp[n]=
return dp[n]=f(n-1)+f(n-2);
}
int main(){
//2.初始化记忆化数组
memset(dp,-1,sizeof(dp));
cout<<f(19);
return 0;
}题目
01背包
01 背包,即一种 DP 问题,以放置物品为模型,每个物品只能放一次

题目解题
递归分治
分而治之:将问题分解为若干子问题,递归解决子问题,最后合并结果无记忆化:子问题可能被重复计算,导致效率低下
特点
自顶向下:从原问题出发,逐步分解为子问题可能重复计算:同一子问题会被多次求解(这个背包问题)
代码直观:直接反映问题逻辑,但时间复杂度高
dfs(1,0)往右,表示对第一个物品选,到dfs(2,1)表示第一个物品选了,虽然参数是2,但第二个物品还没有选
这个dfs不是当前的状态,而是当前选完之后会进入到的状态
(代码中,我的变成习惯是从1开始到i<=N,所以第一个物品在索引为1的位置,别的代码可能在索引为0的位置)
代表选的ans2的ans2=dfs(u+1,sum+v[u])+w[u]是递归(题中是价值)返回值的累加
如:dfs(4,5),因为选了第三个物品,第三个物品的价值是四,把4带回去
代码
不用记忆化搜索(时间复杂度2^n,超时)
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int w[N],v[N];
int n,m;
int dfs(int u,int sum) {
//u代表当前选择的是第几个物品
//sum表示当前的总体积,用当前体积隔离不同递归层的状态,没有(用数组的)显式回溯的使用
//递归函数返回值代表最大价值
if(u>n) {
return 0;
}
//ans1不选,ans2选
int ans1=0,ans2=0;
//ans1不选,直接跳过第u个物品,
ans1=dfs(u+1,sum);
//ans2选第u个物品,并增加价值 w[u]
//这里的ans2=dfs(u+1,sum+v[u])+w[u]是递归返回值的累加
if(sum+v[u]<=m) ans2=dfs(u+1,sum+v[u])+w[u];
return max(ans1,ans2);
}
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>v[i]>>w[i];
cout<<dfs(1,0);
}使用记忆化搜索
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int w[N],v[N];
//1.定义记忆化数组,参数和递归函数参数一样
int dp[N][N];
int n,m;
int dfs(int u,int sum) {
//u代表当前选择的是第几个物品
//sum表示当前的总体积
//递归函数返回值代表最大价值
if(u>n) {
return 0;
}
//3.搜索的时候记忆
// - 在递归边界下判断当前状态是否访问过,访问过,直接返回
if(dp[u][sum]!=-1) return dp[u][sum];
//ans1是不选,ans2是选
int ans1=0,ans2=dfs(u+1,sum);
if(sum+v[u]<=m) ans1=dfs(u+1,sum+v[u])+w[u];
// - 没访问过,正常搜索,记忆下来
return dp[u][sum]=max(ans1,ans2);
}
int main() {
//2.初始化记忆化数组为 -1
memset(dp,-1,sizeof(dp));
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>v[i]>>w[i];
cout<<dfs(1,0);
}使用动态规划
01背包问题,也是选与不选的问题,可以通过子集枚举枚举出来,但是子集枚举时间复杂度为2^n,很高

如果不选,就从上面转移过来,如果选
看选这个物品和不选这个物品那个是最优的
dp[ i ][ j ]=max(dp[ i-1 ][ j-v[ i ]]+w[ i ],dp[ i-1 ][ j ]);
如图:对于dp[ 2 ][ 2 ],选是从dp[ 1 ][ 0 ]过来,不选是从dp[ 1 ][ 2 ]过来
所以代码中选要 j-v[ i ]
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int dp[N][N];
int n,m;
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
//第一维枚举每件物品
for(int i=1;i<=n;i++){
//第二维枚举体积
for(int j=0;j<=m;j++){
if(j<v[i]){
//如果容积不够,不能选
dp[i][j]=dp[i-1][j];
}else{
//容积够,能选这个物品
//看选这个物品和不选这个物品那个是最优的
dp[i][j]=max(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);
}
/*优化
//默认不选
dp[i][j]dp[i-1][j];
if(j>=v[i]){
//当容积允许选第i件物品时,才选
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
}
*/
}
}
cout<<dp[n][m];
return 0;
}数组分割(没看)

#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int a[N];
int dp[N][2];//统计奇偶性
int n;
const int mod=1000000007;
int dfs(int u,int sum) { //前u个数中选出奇偶性为1/0
if(u>n) {
//如果奇偶性总和sum是0,是偶数,return 1;是奇数,return 0
return sum==0;
}
if(dp[u][sum]!=-1) return dp[u][sum];
//对数字有选和不选,进行判断
int ans=0;
if(a[u]%2==1) {
//当前这个数是奇数
//dfs(u+1,sum^1),选这个数
//如果当前的数是奇数,奇数+奇数就是偶数,奇偶性sum变成0
//dfs(u+1,sum),不选这个数
ans=ans+dfs(u+1,sum^1)+dfs(u+1,sum);
} else {
//当前这个数是偶数
//dfs(u+1,sum),奇数选偶数奇偶性不变
//dfs(u+1,sum),不选这个数,奇偶性也不便
ans=ans+dfs(u+1,sum)+dfs(u+1,sum);
}//可以合二为一,直接写成dfs(u+1,sum^(a[u]%2))+dfs(u+1,sum);
return dp[u][sum]=ans%mod;
}
void solve() {
int sum=0;
cin>>n;
for(int i=1; i<=n; i++)
//只关注奇偶性,范围缩小
for(int i=1; i<=n; i++) {
//多组测试数据,手动初始化dp
dp[i][0]=dp[i][1]=-1;
int x;
cin>>x;
x%=2;
a[i]=x;
sum+=a[i];
}
//总和为奇数,只能拆成一组偶数,用一组奇数,不能拆成两组都为偶数
if(sum%2==1) {
cout<<"0\n";
return;
}
cout<<dfs(1,0);
}
int main() {
int t;
cin>>t;
while(t--) solve();
return 0;
}动态规划
动态规划,O(n)=n^3,对于n<=100的情况下使用的算法
动态规划的特点:
有后效性,当前的决策会影响到后面的决策。具有最优子结构的特征
解这类题的步骤:
1.定义数组(数学归纳法中的定义函数):如dp[i](dp代表方案)表示的是什么,时刻记住定义的数组的含义2.初始化dp:初始化dp,初始化的方法有两种:根据数组定义来写或根据实际意思。
3.遍历所有的情况:用子结构递推到最终的结果
4.写状态转移方程:dp[i]由前一个怎样转移过来的
题目
李白打酒加强版(三维dp)


#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int NN=110;
//1.定义数组
//含义:dp是前i个店遇到j朵花,剩k斗酒的方案
int dp[NN][NN][NN];//三维dp数组
int n,m;
int main()
{
cin>>n>>m;
//2.初始化
//这里根据数组定义写
//题目:一天,他提着酒壶,从家里出来,酒壶中有酒 2 斗,所以遇0店0花有2酒方案数是1
dp[0][0][2]=1;
//3.遍历所有的情况
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m-1;j++)
{
if(i==0&&j==0) continue;
for(int k=0;k<=100;k++)//因为最多出现100次操作2,故va最大为100
{
//4.写状态转移方程:dp[i]由什么转移过来
//i代表店,逢店加一倍。所以对于i-1时,是从k/2的状态转移到k的
//因为i-1,所以i>=1。因为k/2,所以k要是偶数
if(k%2==0&&i>=1) dp[i][j][k]=(dp[i][j][k]%mod+dp[i-1][j][k/2]%mod)%mod;
//j代表花,遇花喝一斗。所以对于j-1,是从k+1的状态转移到k的
if(j>=1) dp[i][j][k]=(dp[i][j][k]%mod+dp[i][j-1][k+1]%mod)%mod;
}
}
}
//最后的结果,题目:最后一次遇到的是花,他正好把酒喝光了
//即对于花m-1的情况,还有1酒
cout<<dp[n][m-1][1]%mod;
}跳石头(使用bitset的dp)

#include <bits/stdc++.h>
using namespace std;
const int NN=4e4+10;
/*
这个数组的大小是 MAXN,即数组有 MAXN 个元素
而数组中的每个元素的类型是 bitset<MAXN> 。即,数组的每个元素本身都是一个 bitset 对象
每个这样的 bitset 对象可以存储 MAXN 个二进制位
*/
bitset<NN> dp[NN];
int c[NN];
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>c[i];
int ans=0;
//动态规划的依赖关系:dp [j] 依赖于 dp [j + c [j]] 和 dp [2*j],即 后面的状态会影响前面的状态
//如果从 j = 1 开始,dp[j + c[j]] 和 dp[j * 2] 可能还未计算,导致错误
for(int j=n;j>=1;j--){
/*
bitset 的本质是 二进制位数组,每一位只能是 0 或 1
f因此,dp[j][c[j]] = 1 就是在 dp[j] 的二进制位中,把第c[j]位设为1,表示这个数字可以被访问
*/
dp[j][c[j]]=1;
/*
dp[j + c[j]] 存储了从位置 j + c[j] 出发能到达的状态集合,dp[2*j] 存储了从位置 2*j 出发能到达的状态集合
通过按位或操作,将这些状态集合合并到 dp[j] 中
即从位置 j 出发不仅能到达自身直接能到达的状态,还能到达通过 j + c[j] 或 2*j 这些位置能到达的状态
*/
if(j+c[j]<=n)dp[j]|=dp[j+c[j]];
if(2*j<=n)dp[j]|=dp[2*j];
/*
利用 bitset 的 count() 函数统计 dp[j] 中值为 1 的位的数量
即从位置 i 出发能到达的不同状态的数量
通过不断更新 ans 取最大值,最终得到小明最多能获得的分数
*/
ans=max(ans,(int)dp[j].count());
}
cout<<ans;
return 0;
}dijkstra(最短路)
图-最短路径-Dijkstra(迪杰斯特拉)算法_哔哩哔哩_bilibili
dijkstra算法求单元最短路问题,即图中某一确定的点到另一点的最短路
使用堆(优先队列)时,堆能够自动依据距离对所有点进行排序。在每一轮迭代时,直接从堆顶取出当前距离源点最近的点

邻接表存储图(额外)
//用邻接表存图
int h[NN],e[NN],ne[NN],w[NN],idx;
void add(int a,int b,int c){
w[idx]=c;e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}dijkstra模板
#include <bits/stdc++.h>
using namespace std;
//注意:对于无向图,边的存储量是实际的2倍,看情况提高最大值
const int NN= ;
int n,m;
typedef pair<int,int> PII; //first存距离,second存结点编号
//dist储从起点(源点)到各个结点的当前最短距离
//st标记某个结点的最短距离是否已经确定
int dist[NN],st[NN];
//用邻接表存图
int h[NN],e[NN],ne[NN],w[NN],idx;
void add(int a,int b,int c) {
w[idx]=c;
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int dijkstra() {
memset(dist,0x3f,sizeof(dist)); // 将所有距离初始化正无穷
priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆
dist[1] = 0; // 第一个点到起点的距离为 0
//把 1 号点放入堆中,0代表到1号点的最短路径,1是坐标
heap.push({0,1});
while(!heap.empty()) { // 堆不空
//找到当前距离最小的点
auto p = heap.top();
heap.pop();
//second就是点的编号,如果这个点的最短路确定了,就不用更新其他点了
if(st[p.second]) continue;
st[p.first] = true;//标记p已经确定最短路
// 遍历节点 p.second 的所有邻边(p.second 是当前距离起点最近的节点)
for(int i = h[p.second]; i != -1; i = ne[i]) {
// e[i] 是当前边的终点(即 p.second 的邻居节点)
int j = e[i];
// 如果从起点到 j 的当前最短距离 > 从起点到 p.second 的最短距离 + 当前边的权重
if(dist[j] > dist[p.second] + w[i]) {
// 更新到 j 的最短距离
dist[j] = dist[p.second] + w[i];
// 将 {新距离, 节点j} 加入堆
heap.push({dist[j], j});
}
}
}
// 说明 1 和 n 是不连通的,不存在最短路
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main() {
//h 数组存储的是每个顶点的第一条边在 e 数组中的索引
//若 h[i] 为 -1,则表示顶点 i 没有出边
memset(h,-1,sizeof(h));
cin >> n >> m;
while(m--) {
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
//add(b,a,c); //如果题目要求双向,再来add
}
cout << dijkstra();
return 0;
}题目

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
//注意:对于无向图,边的存储量是实际的2倍
const int NN=2e5+10;
int n,m;
int a[NN];
typedef pair<int,int> PII; //first存距离,second存结点编号
int dist[NN],st[NN];
//用邻接表存图
int h[NN],e[NN],ne[NN],w[NN],idx;
void add(int a,int b,int c){
w[idx]=c;e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
int dijkstra(){
memset(dist,0x3f,sizeof(dist)); // 将所有距离初始化正无穷
priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆
//把 1 号点放入堆中,0代表到1号点的最短路径,1是坐标
heap.push({0,1});
dist[1] = 0; // 第一个点到起点的距离为 0
while(!heap.empty()) // 堆不空
{
//找到当前距离最小的点
auto p = heap.top();heap.pop();
//second就是点的编号,如果这个点的最短路确定了,就不用更新其他点了
if(st[p.second]) continue;
st[p.second] = true;//标记p已经确定最短路
//i赋值成头节点,一直遍历到下一条边
for(int i = h[p.second]; i!=-1; i=ne[i]){
//取出这个节点孩子的编号
int j = e[i];
//题目中:dist[j]是未确定的最短路的点,w[i]是路程的时间,a[j]是隔离的时间
if(dist[j] > dist[p.second] + w[i]+a[j]){
dist[j] = dist[p.second] + w[i]+a[j];
heap.push({dist[j],j}); //入堆
}
}
}
// 说明 1 和 n 是不连通的,不存在最短路
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
//h 数组存储的是每个顶点的第一条边在 e 数组中的索引
//若 h[i] 为 -1,则表示顶点 i 没有出边
memset(h,-1,sizeof(h));
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
while(m--){
int x,y,z;cin>>x>>y>>z;
//x,y是两个顶点,z是权重,题目要求路线双向,所以两个add构建无向图
add(x,y,z);
add(y,x,z);
}
//到第n个城市不需要隔离,要把n减掉
int res=dijkstra();
if(res!=-1)cout<<res-a[n];
return 0;
}数学
求最大公因数(最大公约数)
欧基里得算法(辗转相除法)
BV19r4y127fu
公约数(公因数):一个能被若干个整数同时均整除的整数
- 求 A 和 B 的最大公因数,除法关系
- (A,B)=(B,R)
- 求到最后,R=0,B 就是最大公因数

//求最大公因数
int GCD(int a,int b){
if (a%b==0)return b;
else return GCD(b,a%b);
}求最小公倍数
- 两个数相乘,然后除以它们的最大公因数
//求最小公倍数
int LCM(int a,int b){
return ((a*b)/GCD(a,b));
}C++17自带lcm函数
分解质因数
给定正整数,打印出所有的因数都是质数
对正整数n进行分解质因数,先找到一个最小的质数
1.该正整数n为质数,则说明不需要分解
2.如果该正整数n不是质数,但是能被最小的质数整除,就打印最小的质数,然后从正整数n除以最小质数,作为新的正整数重复执行1和2
从小到大遍历 i
循环从 i=2 开始,逐步增加 i
由于 i 从小到大遍历,第一个满足 x % i == 0 的 i 一定是 x 的最小质因数:
如果 i 是合数,它一定已经被更小的质因数分解过:
例如 i=4:
如果 x % 4 == 0,说明 x 是 4 的倍数。
但 4 本身可以分解为 2*2,所以 x 一定已经被 i=2 分解过。
因此,x 不可能再被 4 整除(因为 2 已经分解完了)
结论:i 只会是质数,因为合数因数已经被更小的质因数分解
if(n>1):
处理可能剩余的大于sqrt(n)的质因数
假设输入 n = 15
首先,i = 2,15 % 2 != 0,不执行内层循环。
接着,i = 3,15 % 3 == 0,进入内层循环,n 变为 5
此时,i = 4,4 * 4 > 5,外层循环结束
此时 n = 5 > 1,需要处理
//分解质因数核心步骤
//用 i*i <= n 动态判断,整数运算更快,用i<=sqrt(n)慢
for(int i=2;i*i<=n;i++){
//确认当前的 i 是否为 n 的因数。只有当 n 能被 i 整除时,i 才有可能是 n 的质因数
if(n%i==0){
//内层的 while 循环来进一步分解 n 中包含的所有 i 因子
while(n%i==0){
n/=i;
}
}
}
// 处理可能剩余的大于 sqrt(n) 的质因数
if(n>1){
//...
}唯一分解定理(额外)
完全平方数

题目解析
由唯一分解定理:任何一个数,都可以分解成若干个质数的乘积
如果这个数是完全平方数,那么这若干个质数的指数一定是偶数
对于本题,需要记录指数不是偶数的数字
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int n;cin>>n;
map<int,int>mp;
//分解质因数
for(int i=2;i*i<=n;i++){
while(n%i==0){
n/=i;
//这里i就是分解出来的质因子
//把 n 中包含的 i 因子去除,然后将 mp[i] 的值加 1,以此记录 i 作为质因数出现的次数
mp[i]++;
}
}
if(n>1)mp[n]++;
int ans=1;
for(auto i:mp){
//如果分解出的质因子只出现了一次
if(i.second%2==1)ans*=i.first;
}
cout<<ans;
return 0;
}判断素数(欧拉筛法)
质数,又称素数,除了1和该数自身外,无法被其他自然数整除的数
1既不是质数(素数)也不是合数
平方根法(欧拉筛法)判断素数:
对于一个数字 n,根号n*根号n=n
因数是关于根号 n 对称分布的
所以只需要遍历到根号 n,如果在根号n内没有因数,那么之后也没有了
bool isPrime(int num) {
//有的题目,传入的num就直接从2开始,这个if(num<2)可以不写
if (num < 2) return false;
//不要写sqrt,比i*i慢
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
}模运算性质(额外)
对于减法的取模,在成为负数时,要再加上p

快速幂
蓝桥云课-快速幂
BV1nd4y1A7vF
n&1:
判断n的二进制形式最后一位是否为1
//这个mod可以不用
ll qmi(ll a,ll n,ll mod) { //计算a^n
ll ans=1;//用ans返回结果
while(n) { //把n看成二进制,逐个处理它的最后一位
if(n&1)ans=ans*a%mod;//n的最后一位是1表示这一位要计算,需要乘a,这个mod自己定义,1000或某个数
a=a*a%mod;//加倍,a^2->a^4->a^8...
n>>=1;//n右移1位,把n的最后一位去掉
}
return ans;
}
乘法逆元
乘法逆元
BV195411w75c
视频里还讲了p不是质数的情况,用扩展欧几里得算法
但题目中一般是10^9+7

欧拉算法
题目
最大公约数

筛质数

#include <bits/stdc++.h>
using namespace std;
//不要用sqrt,比用i*i慢
bool isPrime(int num) {
if (num < 2) return false;
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
}
int n;
int cnt=0;
int main()
{
cin>>n;
//1既不是质数(素数)也不是合数,遍历从2开始
for(int i=2;i<=n;i++){
if(isPrime(i))cnt++;
}
cout<<cnt;
return 0;
}分解质因数
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
void divide(int n){
cout<<n<<"=";
for(int i=2;i*i<=n;i++){
if(n%i==0){
while(n%i==0){
cout<<i;
n/=i;
//如果还有剩余,输出乘号
if(n>1)cout<<"*";
}
}
}
// 处理剩余的质数
if(n>1)cout<<n;
cout<<endl;
}
int a,b;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>a>>b;
for(int i=a;i<=b;i++)divide(i);
return 0;
}快速幂
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll qmi(ll a,ll n,ll mod){
ll ans=1;
while(n){
if(n&1)ans=ans*a%mod;
a=a*a%mod;
n>>=1;
}
return ans;
}
ll b,p,k;
int main()
{
cin>>b>>p>>k;
cout<<qmi(b,p,k);
return 0;
}乘法逆元
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl '\n'
ll p=1e9+7;
int T;
ll qmi(ll a,ll n){
ll ans=1;
while(n){
if(n&1)ans=ans*a%p;
a=a*a%p;
n>>=1;
}
return ans;
}
int main()
{
cin>>T;
while(T--){
ll N;
cin>>N;
cout<<qmi(N,p-2)<<endl;
}
return 0;
}高斯求和
高斯求和是一种快速计算连续整数和的方法

同余定理
给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余
记作a≡b(mod m)
a 和 b 除以 m 后的余数相同,即a-b是m的倍数(m能整除a-b)
即,如果a%m==b%m,(a-b)%m==0
两个数模 m 同余,所以它们的差能被 m 整除
题目
k倍区间(前缀和,同余定理,组合数)

题目解析
k=2,对1 2 3 4 5这个序列求前缀和
然后再对k进行取余
已知同余定理:对于余数相同的两个数字,它们的差能被某个正整数k整除(a≡b(mod k))
在这里,“它们的差”就是区间和(用前缀和求差就是求区间和)
而这个区间和能被k整除,符合题目要求
所以要计算不同余数,相同的次数出现了几次
然后用组合数的基本定义(组合数的基本定义是阶乘的方式,和递推公式数学本质一样)求有几个区间
因为是在出现相同余数的前缀和中选两个,即在出现的同余次数中选两个
所以公式为n(n-1)/2
对于两个不同的模 K 为 0 的前缀和,它们之间的子数组和是 K 的倍数,这样的组合数可以用组合公式 C(n, 2) = n * (n - 1) / 2 计算(从 n 个元素中选 2 个的组合数)
但是,单个模 K 为 0 的前缀和本身也算一种满足条件的情况,所以需要额外加上这 n 种情况。而 n * (n - 1) / 2 + n = n * (n + 1) / 2
代码
AC
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int N,K;
const int NN=1e5+10;
int a[NN];
ll prefix[NN];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>N>>K;
map<int,int>mp;
for(int i=1;i<=N;i++){
cin>>a[i];
//对每一个前缀和取模
prefix[i]=(prefix[i-1]+a[i])%K;
//计算不同余数出现的次数
mp[prefix[i]]++;
}
ll ans=0;
for(auto i:mp){
//组合数C(n,2)=n(n-1)/2
if(i.first==0){
//ans+=i.second*(i.second+1)/2;//简写
ans+=(ll)i.second*(i.second-1)/2+i.second;
}
else ans+=(ll)i.second*(i.second-1)/2;
}
cout<<ans;
return 0;
}暴力(只通过2个)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int N,K;
const int NN=1e5+10;
ll a[NN],prefix[NN];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>N>>K;
for(int i=1;i<=N;i++){
cin>>a[i];
prefix[i]=prefix[i-1]+a[i];
}
int cnt=0;
//求区间,O(n^2)
for(int i=1;i<=N;i++){
for(int j=i;j<=N;j++){
if((prefix[j]-prefix[i-1])%K==0)cnt++;
}
}
cout<<cnt;
return 0;
}等差数列

等差数列求和
题目要求中包含连续的正整数相加,这就可以联想到等差数列求和公式
判断是否是2^n
bool check(int n){
//如果是2^n,一直除2,最后会等于1,所以在n=1是循环停止,循环进行条件是n!=1
while(n!=1){
//n为偶,除2
if(n%2==0)n/=2;
//n是奇数且不等于1(比如 3、5 等),返回false,因为它不可能是2的幂次方数
else return false;
}
return true;
}题目
等差数列

题目分析
题目要求项数最少,即公差 d 最大。
而由于等差数列的任意两项之差都是公差的倍数,所以我们只需要求出给出的数两两之差的最大公因数即可
代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN=1e5+10;
int a[NN];
int n;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
sort(a+1,a+n+1);
if (a[1] == a[n]){
//公差d为0的情况
//都排完序了第一个和最后一个还是相等
//肯定是全部都相等,直接结束
cout << n << endl;
return 0;
}
int d = a[2] - a[1];//初值设为一个公差的若干倍
for (int i = 3; i <= n; i++)
d = __gcd(d, a[i] - a[i - 1]);
cout << (a[n] - a[1]) / d + 1 << endl;//求项数
return 0;
}数字诗意

#include <bits/stdc++.h>
using namespace std;
#define int long long
bool check(int n){
while(n!=1){
if(n%2==0)n/=2;
else return false;
}
return true;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int n;cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int x;cin>>x;
if(check(x))ans++;
}
cout<<ans;
return 0;
}并查集
BV1Bh4y1k7fZ
用并查集或者bfs求连通块
并查集也可以判断两个点在不在同一个集合(就是判断两个点连不连通)
并查集优化方式有:

题目
并查集

朴素代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN=1e5+10;
//父节点是前一个节点
int pre[NN];
//函数命名成root,因为并查集,查的是元素的根节点,而且避免和stl中的find重名
int root(int x){
//朴素写法
//当 pre[x]=x 时,说明x的父节点就是它自身,此时x就是所在集合的根节点,直接返回 x
//x不是根节点,传入pre[x],继续查找 x 的父节点的根节点,直到找到根节点为止
//return pre[x]==x?x:root(pre[x]);
//路径压缩优化
//找到节点x的根节点后,将节点x的父节点直接设置为根节点,实现了路径压缩
return pre[x]=pre[x]==x?x:root(pre[x]);
}
void merge(int x,int y){
//此时,x和y代表的是两个集合的根节点
x=root(x),y=root(y);
//x和y的根节点相同,已经在同一个集合中,此时不需要进行合并操作,直接返回
if(x==y)return;
//x和y不相等,分别属于不同的集合。将x的父节点设置为y(将y的父节点设置为x没区别)
pre[x]=y;
}
void solve(){
int n,m;
cin>>n>>m;
//初始化,把每个节点变成自己的父节点(自环)
for(int i=1;i<=n;i++) pre[i]=i;
while(m--){
int op,x,y;
cin>>op>>x>>y;
//如果操作是1,合并
if(op==1)merge(x,y);
else cout<<(root(x)==root(y)?'Y':'N')<<endl;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _=1;
while(_--)solve();
return 0;
}
路径压缩(优化)
原本
优化
优化的代码只有一个改动,在朴素代码中注释了
合根植物(是否属于同一个集合)


#include <bits/stdc++.h>
using namespace std;
const int M=1000;
const int N=1000;
//父节点
int pre[M*N];
int m,n,k;
int root(int x){
return pre[x]=pre[x]==x?x:root(pre[x]);
}
void merge(int x,int y){
x=root(x);y=root(y);
if(x==y)return;
pre[x]=y;
}
void solve(){
cin>>m>>n>>k;
for(int i=1;i<=m*n;i++)pre[i]=i;
while(k--){
int a,b;
cin>>a>>b;
merge(a,b);
}
int cnt=0;
for(int i=1;i<=n*m;i++){
//如果根节点等于自身,说明没有成为别人的子节点
if(root(i)==i)cnt++;
}
cout<<cnt;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _=1;
while(_--)solve();
return 0;
}修改数组(先把所有可能都设置成父节点,是否出现过,出现就修改)
题目

题目分析



代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN=1e5+10;
int pre[NN];
int N;
int root(int x){
return pre[x]=pre[x]==x?x:root(pre[x]);
}
void merge(int x,int y){
x=root(x);y=root(y);
if(x==y)return;
pre[x]=y;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>N;
for(int i=1;i<=1e5+5;i++){
pre[i]=i;
}
int A;
for(int i=1;i<=N;i++){
cin>>A;
A=root(A);//找到A的根节点
cout<<A<<' ';
merge(A,A+1);//将A与A+1相连
}
return 0;
}字符串
isdigit(c)检查是否是数字字符
和c<='9'&&c>='0'效果一样
数字字符-'0'得到原本的数字
to_string(把十进制整数和浮点变成字符串)
stoi(返回对应字符串内容的整数值)
reverse(s.begin(),s.end())反转
sort(s.begin(),s.end())按字典序排序
toupper和tolower
把字符串全部转成大写或者小写
substr截取字符串
字符串基本操作
// string str1; //生成空字符串
// string str2("123456789"); //生成"1234456789"的复制品
// string str5(5, '1'); //结果为"11111"
// 尾插一个字符s1.push_back('a');
//但是对于字符串,+就是连接,可以直接s1+='a',这个push_back()没用
//插入字符找迭代器
//str.insert(s.begin()+i,'a')如果前面是s.begin()+i那么只能插入字符;
//插入字符串找下标
// str.insert(pos,"string"如:cs):在指定的位置pos插入字符串;
//string s1 = "123456789";
// s1.erase(s1.begin()+1); // 结果:13456789
// s1.erase(1);//删除1,包括1以后的所有值;//结果:1
// s1.erase(s1.begin()+1,s1.end()-2); // 结果:189//都是闭区间
// s1.erase(2,2); 从第二个位置开始是删除2后边的2个位置 // 结果:1256789
//转置字符串
// reverse(s.begin(),s.end());string str=s;
//string s("dog bird chicken bird cat");
//字符串查找-----找到后返回首字母在字符串中的下标
// 1. 查找一个字符串
// if(s.find("chicken",0)!=string::npos) //代表从0下标开始,没有找到返回string::npos(通常是 4294967295 或 18446744073709551615,取决于系统)
//cout << s.find("chicken") << endl; // 结果是:9
// 2. 从下标为6开始找字符'i',返回找到的第一个i的下标
//cout << s.find('i',6) << endl; // 结果是:11
//tring s1("0123456789");
//string s2 = s1.substr(2,5);
// 结果:23456-----参数5表示:截取的字符串的长度题目
记数问题(数字字符-'0',to_string)

#include <bits/stdc++.h>
using namespace std;
int n,x;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n>>x;
int cnt=0;
for(int i=1;i<=n;i++){
string s=to_string(i);
for(int i=0;i<s.size();i++){
if(s[i]-'0'==x)cnt++;
}
}
cout<<cnt;
return 0;
}统计单词数
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//读入两行
getline(cin,s1);
getline(cin,s2);
//全部转成大写,方便判断
for(int i=0;i<s1.size();i++) s1[i]=toupper(s1[i]);
for(int i=0;i<s2.size();i++) s2[i]=toupper(s2[i]);
//要找给定的单词,单词是独立的,即这个单词左右两边都有空格
s1=' '+s1+' ';
//把句子的开头和结尾增加空格,方便找到出现在开头或结尾的单词
s2=' '+s2+' ';
//没有找到返回-1
if(s2.find(s1)==-1){
cout<<-1;
}else{
int cnt=0;
//这个单词第一次出现的开始位置
int st=s2.find(s1);
int pos=st;
while(pos!=string::npos){
cnt++;
//要找单词有多少个,即每次找到单词的位置pos之后,再从下一个位置往后找,每次找到次数cnt++
pos=s2.find(s1,pos+1);
}
cout<<cnt<<' '<<st;
}
return 0;
}结构体
题目

#include <bits/stdc++.h>
using namespace std;
const int NN=1010;
int N;
struct Node{
string name;
int chinese,math,eng;
int sum;
int idx;
}stu[NN];//直接用Node类型声明数组stu
bool cmp(Node a,Node b){
if(a.sum!=b.sum) return a.sum>b.sum;
else return a.idx<b.idx;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>N;
for(int i=1;i<=N;i++){
string name;
int x,y,z;cin>>name>>x>>y>>z;
stu[i]={name,x,y,z,x+y+z,i};
}
//自定义排序
sort(stu+1,stu+1+N,cmp);
cout<<stu[1].name<<' '<<stu[1].chinese<<' '<<stu[1].math<<' '<<stu[1].eng;
return 0;
}输入输出
getchar()获取空字符
scanf读时间/日期
用scanf读要把流关闭
scanf可以按照一定的格式读入数据。读入整数用%d,读入long long 用%lld
printf("%02d\n",a),表示输出2位数字,没有两位就补前导0
题目
日期问题
set、map、priority_queue 等容器在存储自定义结构体时,必须知道如何比较元素(默认按 < 排序)
operator<用于 set 去重和排序:set 会自动根据 < 排序,并保证元素唯一

#include <bits/stdc++.h>
using namespace std;
struct Node {
int year, month, day;
// set对于自定义的结构体,要定义比较运算符,用于排序
bool operator<(const Node& other) const {
//返回year成员较小的对象为true
if (year != other.year) return year < other.year;
//返回month成员较小的对象为true
if (month != other.month) return month < other.month;
//返回day成员较小的对象为true
return day < other.day;
}
};
bool leap(int year) {
return (year % 400 == 0) || (year % 4 == 0 && year % 100 != 0);
}
int main() {
int x, y, z;
//用scanf读取日期
scanf("%d/%d/%d", &x, &y, &z);
//题目要求不相同的日期,所以去重
set<Node> st;
int months[] = {-1, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
for (int year = 1960; year <= 2059; year++) {
// 每次年份循环时设置2月天数
months[2] = leap(year) ? 29 : 28;
for (int month = 1; month <= 12; month++) {
for (int day = 1; day <= months[month]; day++) {
// 检查三种可能的日期格式
if ((x == year % 100 && y == month && z == day) ||
(x == month && y == day && z == year % 100) ||
(x == day && y == month && z == year % 100)) {
st.insert({year, month, day});
}
}
}
}
// 输出结果
for (auto i : st) {
//02:输出至少两位,不足补0
printf("%d-%02d-%02d\n", i.year, i.month, i.day);
}
return 0;
}航班时间


#include <bits/stdc++.h>
using namespace std;
int f(){
int h1,h2,m1,m2,s1,s2;
scanf("%d:%d:%d %d:%d:%d",&h1,&m1,&s1,&h2,&m2,&s2);
int day=0;
if(getchar()==' '){
scanf("(%d)",&day);
}
//把去程/回程花费时间变成秒
return (day*24*3600+h2*3600+m2*60+s2)-(h1*3600+m1*60+s1);
}
int main(){
int n;scanf("%d",&n);
while(n--){
int sec=(f()+f())/2;
//一小时3600秒,总的秒/3600=小时
//一分钟60秒,总的秒%3600/60=分钟(总的秒%3600就是不超过一个小时的秒数)
//总的秒%60=秒(总的秒%60就是不超过一个分钟)
printf("%02d:%02d:%02d\n",sec/3600,sec%3600/60,sec%60);
}
return 0;
}getline(cin,a)获取整行

while(cin>>a[++cnt])全读,忽略空格换行
题目

#include <bits/stdc++.h>
using namespace std;
const int NN=110;
int a[NN];
int N;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//这个代表行数的N没有用,因为while(cin>>a[++cnt]);跳过空格换行
cin>>N;
int cnt=0;
//一直输入,++cnt,先++,让数组从下标1开始
while(cin>>a[++cnt]);
sort(a+1,a+cnt+1);
int m,n;
for(int i=2;i<=cnt;i++){
if(a[i]==a[i-1]+2)m=a[i]-1;
if(a[i]==a[i-1])n=a[i];
}
cout<<m<<" "<<n;
return 0;
}stl

stack
对于出栈,一定要判断是否为空,如果栈为空,出栈会报错

题目
表达式括号匹配

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
string s;cin>>s;
stack<char>st;
for(int i=0;i<s.size();i++){
if(s[i]=='(')st.push('(');
else if(s[i]==')'){
//对于出栈,一定要考虑是否为空,如果栈为空,出栈会报错
if(st.empty()){
cout<<"NO"<<endl;
return 0;
}
st.pop();
}
}
if(st.empty())cout<<"YES"<<endl;
else cout<<"NO"<<endl;
return 0;
}后缀表达式
洛谷P1449 后缀表达式_哔哩哔哩_bilibili
题目解析
变成树,遍历方式:遍历左子树,然后遍历右子树,最后遍历根节点
遇到数字就压栈,遇到符号就出栈运算,把运算后新的数字入栈,依次循环

代码
#include <bits/stdc++.h>
using namespace std;
string s;
stack<int> st;
int l = 0, r = 0;
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin>>s;
for(int i = 0; i < s.size(); i++) {
if(s[i] == '@') break;
if(isdigit(s[i])) {
l = l * 10 + (s[i] - '0');
}
else if(s[i] == '.') {
st.push(l);
l = 0; // 重置临时数字
}
else if(s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/') {
// 注意顺序:左操作数先出栈
l = st.top(); st.pop();
r = st.top(); st.pop();
if(s[i] == '+') {
st.push(l + r);
}
else if(s[i] == '-') {
st.push(r - l); // 注意顺序
}
else if(s[i] == '*') {
st.push(l * r);
}
else if(s[i] == '/') {
st.push(r / l); // 注意顺序
}
l = 0; // 重置
}
}
cout << st.top();
return 0;
}queue
循环问题用队列做比较好
队列先进先出
在循环问题中,最早发现的节点最早被处理
题目
约瑟夫问题

#include <bits/stdc++.h>
using namespace std;
int n,m;
queue<int>que;
int cnt=1;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n>>m;
//把元素放入队列
for(int i=1;i<=n;i++) que.push(i);
while(que.size()){
//首元素保存,然后出队
int first=que.front();que.pop();
if(cnt==m){
//到了规定的此处,出队的元素输出
cout<<first<<" ";
cnt=1;
}else{
//没有到规定的次数,原本出队的元素入队
que.push(first);
cnt++;
}
}
return 0;
}赢球票(循环问题用队列)
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int NN=110;
int a[NN];
int N;
queue<int>que;
int check(int x){
queue<int>empty;swap(que,empty);
//实现轮转数组
for(int i=x;i<=N;i++)que.push(a[i]);//把x后面的数字入队
for(int i=1;i<x;i++)que.push(a[i]);//把x前面的数字入队
int sum=0,cur=1;
while(!que.empty()){
int p=que.front();que.pop();
if(p==cur){
//如果报数和当前值一样,加上
sum+=p;
cur=1;
}else{
//不一样,重新入队(入队操作让圆圈的轮转顺序不变)
que.push(p);
cur++;
}
if(cur>N)break;
}
return sum;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>N;
for(int i=1;i<=N;i++)cin>>a[i];
int ans=0;
for(int i=1;i<=N;i++)ans=max(ans,check(i));
cout<<ans;
return 0;
}priority_queue
优先队列是一种堆
greater,小根堆,从小到大,堆顶是最小的
less,大根堆,从大到小,堆顶是最大的
![]()
题目
合并果子
#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int n;cin>>n;
priority_queue<int,vector<int>,greater<int>>pque;
for(int i=1;i<=n;i++){
int x;cin>>x;
pque.push(x);
}
int ans=0;
//找到大于两堆才进行合并
while(pque.size()>1){
int t1=pque.top();pque.pop();
int t2=pque.top();pque.pop();
ans+=t1+t2;
pque.push(t1+t2);
}
cout<<ans;
return 0;
}map
BV1Bw9GYBEj8
哈希表是一种通过键直接访问值的数据结构,很多语言的map底层基于哈希表实现。哈希表内部由一个数组构成,这个数组中的每个元素(数组项 )被视为一个 “桶”
std::map 提供了高效的查找操作。可以通过 count 函数快速判断某个键是否存在
find函数,指向键等于 key 的元素的迭代器。若找不到这种元素,则返回尾后(end() )迭代器

map自动按照第一个type的字典序,从小到大排序

哈希表的实现
#include <bits/stdc++.h>
using namespace std;
map<int,bool>mp;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int q;
cin>>q;
while(q--){
char op;
int x;
cin>>op>>x;
if(op=='I')mp[x]=true;
else cout<<(mp.count(x)?"Yes":"No")<<endl;
}
return 0;
}密文搜索

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
string s;cin>>s;
map<string,int>mp;
for(int i=0;i<s.size();i++){
string str=s.substr(i,8);
if(str.size()!=8)break;
//获得每一个子串,自己按照字典序手动排序
sort(str.begin(),str.end());
//有相同排序的,就是同一种,直接++
mp[str]++;
}
int n;cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
string str;cin>>str;
//对密码列表进行手动排序
sort(str.begin(),str.end());
//经过排序后,一样的话,加上一样的个数,就是答案
ans+=mp[str];
}
cout<<ans;
return 0;
}set


题目
不重复数字(用set存元素,元素顺序存数组,手动按顺序输出)

用set存数字,虽然可以去重,但是会从小到大排序
可以存数组,让set去重之后,按照数组中数字的顺序
通过count和erase手动按照顺序输出
#include <bits/stdc++.h>
using namespace std;
int T,n;
const int NN=5e4+10;
int a[NN];
void solve(){
cin>>n;
set<int>st;
//这里元素用数组存,应为set会从小到大排序,不能直接存数字
for(int i=1;i<=n;i++){
cin>>a[i];
st.insert(a[i]);
}
for(int i=1;i<=n;i++){
//因为用数组a保存了元素的顺序,让i=1开始遍历,就能按照顺序输出
if(st.count(a[i])){
//如果存在这个数字,输出,然后删除所有相同的元素
cout<<a[i]<<' ';
st.erase(a[i]);
}
}
cout<<endl;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>T;
while(T--)solve();
return 0;
}unordered_set
set有序集合,速度log
unordered_set无序集合,速度c
都是不重复
题目
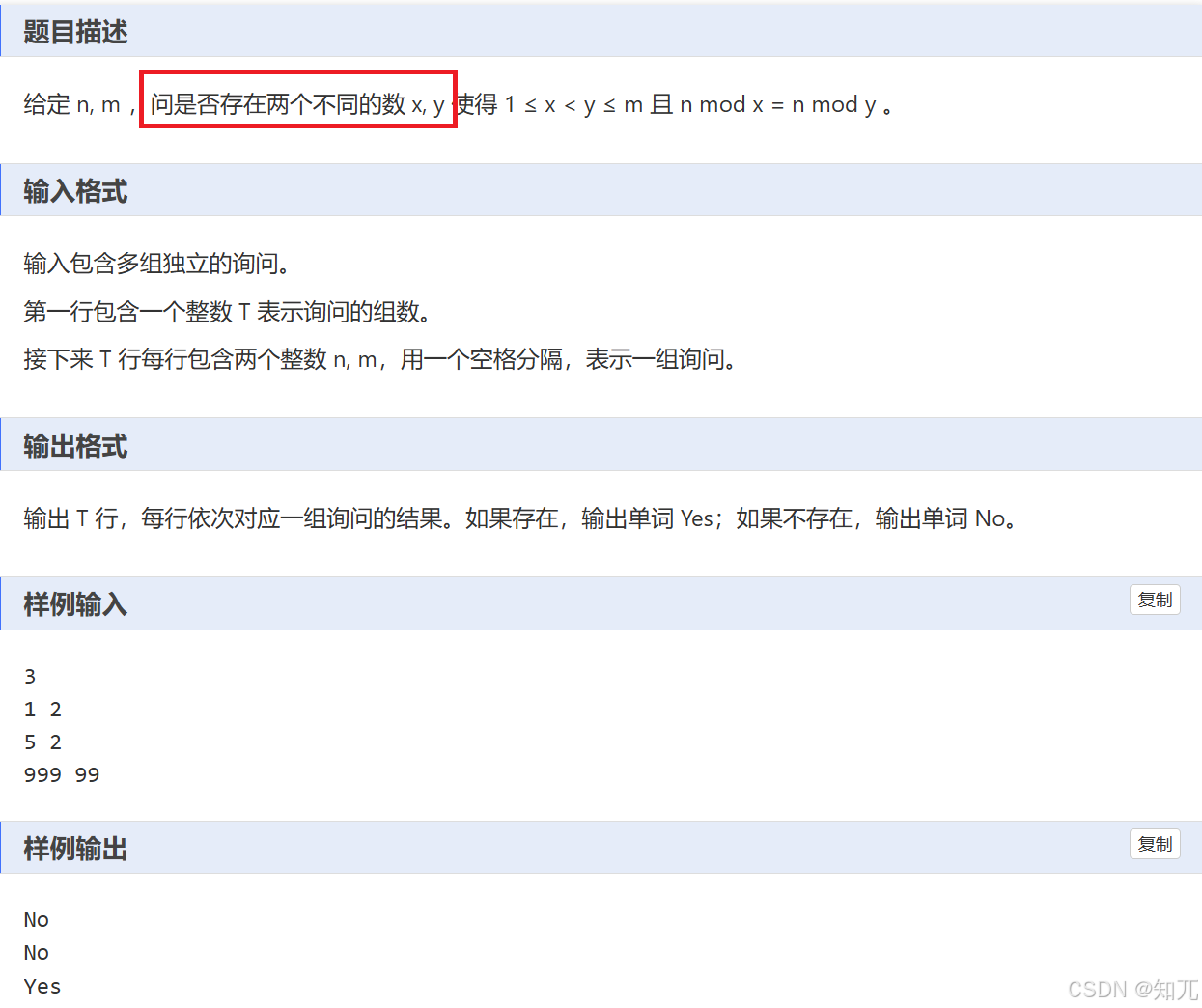
#include <bits/stdc++.h>
using namespace std;
int main(){
int tt;
scanf("%d",&tt);
while(tt--){
int n,m;
scanf("%d %d",&n,&m);
bool flag=false;
unordered_set<int>sett;
for(int i=1;i<=m;i++){
int temp=n%i;
auto it=sett.find(temp);
if(it!=sett.end()){
cout<<"Yes"<<'\n';
flag=true;
break;
}else{
sett.insert(temp);
}
}
if(!flag)cout<<"No"<<'\n';
}
return 0;
}用advance()移动迭代器 (额外)

题目
第k小整数(advance()移动set)

#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int n, k;
cin >> n >> k;
set<int> st;
while(n--){
int x; cin >> x;
st.insert(x);
}
// 输出第k小的元素
if(st.size() < k) {
cout << "NO RESULT";
} else {
auto it = st.begin();
advance(it, k-1); // 移动到第k小的元素
cout << *it;
}
return 0;
}双指针
题目
最长子序列
题目解析
一个指针指向S,一个指针指向T
遍历S,如果S[i]==T[j],j++

代码
#include <bits/stdc++.h>
using namespace std;
string S,T;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>S>>T;
int ans=0;
for(int i=0,j=0;i<S.size()and j<T.size();i++){
if(S[i]==T[j]){
j++;
ans++;
}
}
cout<<ans;
return 0;
}#include <bits/stdc++.h>
using namespace std;
#define int long long
int a,b,n;
int ans=0;
void solve(){
cin>>a>>b>>n;
int cnt=0;
for(int week=1;;week++){
week%=7;
if(week>=1&&week<=5){
cnt+=a;
ans++;
}else{
cnt+=b;
ans++;
}
if(cnt>=n)return;
}
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int _=1;
while(_--)solve();
cout<<ans;
return 0;
}几何
拼正方形
要拼成一个正方形,需要的相同的小正方形的个数必须是完全平方数
题目

题目分析
要使边长尽可能的大,就肯定是要多用 2×2 的方块
我们先用 2×2 的方块拼一个最大正方形
的结果2717561.0183988509662675986152793⋯,向下取整后值为 2717561,因为用的是2*2的方块,所以边长要*2(不然就是用1×1小正方形拼成正方形时的边长),目前正方形最大边长就是 2717561×2=5435122
这时,再用1*1的方块补
到这里要想让边长 +1 就要用 5435122×4+4 个 1×1 的正方形
但是5435122×4+4>10470245,故不能再拼一层
答案
5435122











































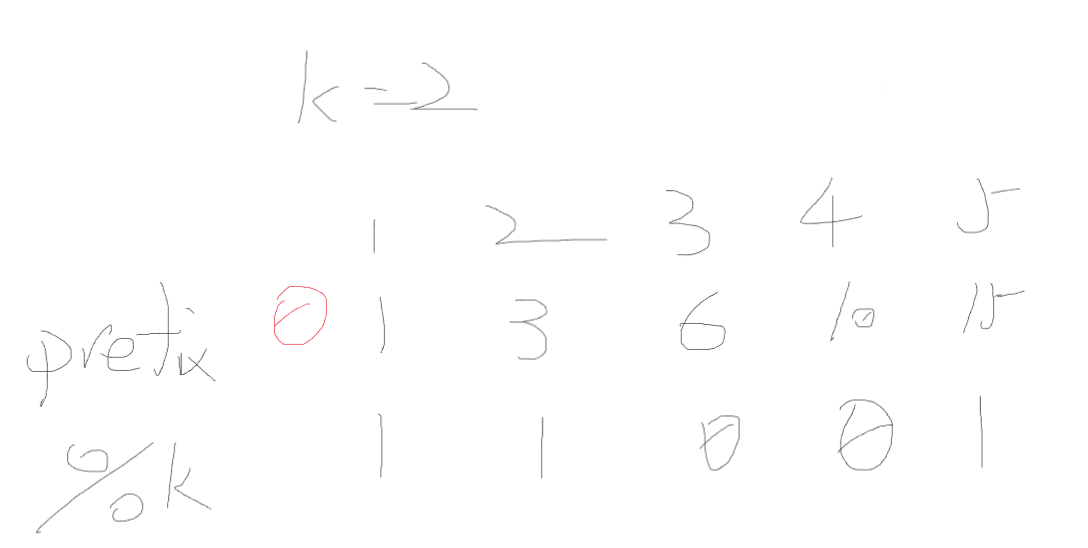


















![[论文阅读] 人工智能 | 利用负信号蒸馏:用REDI框架提升LLM推理能力](https://i-blog.csdnimg.cn/direct/be41d81fe52e4acfbce6f9cf312afd02.png)