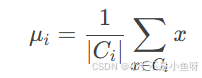采油

题目描述

LQ 公司是世界著名的石油公司，为世界供应优质石油。

最近，LQ 公司又在森林里发现了一大片区域的油田，可以在这个油田中开采 nn 个油井。

LQ 公司在这 nn 个油井之间修建了 n−1n−1 条道路，每条道路连接两个油井，路径中间不会路过任何油井，而且这些道路将所有油井连通。

建立油井的时候需要使用一台大型设备，运输起来非常麻烦，LQ 公司准备在其中的一个油井位置建立一个空运站，先将设备空运到空运站，之后每次经过他们建立的道路来运输这个大型设备以建立不同的油井，当油井建立完毕后再从空运站将大型设备运走。

为了减少运输的麻烦，公司要求大型设备在道路上运输的总路程是最短的。

在建立油井和采油的过程中需要花费一些人力，第 ii 个油井需要花费 BiBi​ 个人，而一旦油井建成，就需要 SiSi​个人一直坚守在油井上进行维护。

当然，如果一个人参与了油井的建设，他可以直接留下来维护油井，或者参与下一个油井的建设，但是在维护油井的人不能再参加后续油井的建设了。

现在 LQ 公司想知道，大型设备运输的总路径长度最短是多少？在保证总路径长度最短的情况下，LQ 公司至少需要花费多少人力才能完成所有油井的建立与维护。

输入描述

输入的第一行包含一个整数 nn ，表示油井的数量。油井由 1 到 nn 依次标号。

第二行包含 nn 个整数，依次表示 B1,B2,...,BnB1​,B2​,...,Bn​，相邻的整数之间用一个空格分隔。

第三行包含 nn 个整数，依次表示 S1,S2,...,SnS1​,S2​,...,Sn​，相邻的整数之间用一个空格分隔。

接下来 n−1n−1 行描述油井之间的道路，其中的第 ii 行包含两个整数 a，ba，b，用一个空格分隔，表示一条道路的起点为 i+1i+1、终点为 aa，长度为 bb，道路是双向的，设备可以从任意一端运送到另一端，每条道路都可以经过任意多次。数据保证任意两个油井之间都可以通过道路连接。

其中，nn 不超过 105105，B、S、cB、S、c 均为不超过 104104 的正整数。

输出描述

输出包含两个整数，用一个空格分隔，表示最优情况下大型设备需要运输的总路程，以及在总路程最短的情况下最少需要花费的人力数量。

输入输出样例

示例

输入

2
10 20
15 15
1 8

输出

16 30

样例说明

有两种方案达到最优。

方案一：在油井 2 建立空运站，先建立油井 2，再将大型设备运输到油井 1 建立油井 1，最后将大型设备运回油井 2。

方案二：在油井 1 建立空运站，先将大型设备运输到油井 2 建立油井 2 ，再将大型设备运送到油井 1 建立油井 1 。

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

总通过次数: 36  |  总提交次数: 65  |  通过率: 55.4%

难度: 困难   标签: 2018, 规律, 思维, 国赛

算法思路

本题需要解决两个关键问题：

1. ​​设备运输总路径​​：在树形油田结构中，设备运输总路径恒等于​​所有边权之和的两倍​​（因为每条边需要往返一次）
2. ​​最少人力花费​​：完成所有油井的建立与维护所需的最小人力为​​所有油井维护人力之和​​（即 ΣS_i），因为维护人员需要长期驻守，而建设人员是临时调配的

算法步骤

1. ​​计算总路径长度​​：

   • 读取所有道路长度
   • 路径总和 = 所有边权之和 × 2

2. ​​计算最少人力​​：

   • 读取所有油井的维护人力 S_i
   • 人力总和 = ΣS_i

C++代码实现：

#include <iostream>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    // 读取油井数量
    int n;
    cin >> n;
    
    // 跳过建设人力B_i（不影响结果）
    for (int i = 0; i < n; i++) {
        int tmp;
        cin >> tmp;
    }
    
    // 计算维护人力总和
    long long total_people = 0;
    for (int i = 0; i < n; i++) {
        int s;
        cin >> s;
        total_people += s;
    }
    
    // 计算道路总长度
    long long total_path = 0;
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b; // a可忽略
        total_path += b;
    }
    total_path *= 2; // 往返路径
    
    // 输出结果
    cout << total_path << " " << total_people;
    return 0;
}

代码解析

1. ​​输入处理​​：

   • n：油井数量
   • 跳过B_i：建设人力不影响最终结果
   • 累加S_i：维护人力总和决定最终花费

2. ​​路径计算​​：

   • 每条道路长度累加后乘以2（往返路径）
   • 使用long long防止溢出（最大路径 2e9）

3. ​​输出格式​​：

   • 先输出设备总路径
   • 再输出维护人力总和

实例验证

​​输入样例​​：

2
10 20
15 15
1 8

​​计算过程​​：

• 路径总和：8 × 2 = 16
• 维护人力：15 + 15 = 30
• ​​输出​​：16 30

注意事项

1. ​​数据范围​​：

   • n ≤ 10^5：需用long long存储路径总和
   • 边权 ≤ 10^4：最大路径 2×10^5×10^4 = 2×10^9

2. ​​输入顺序​​：

   • 第二行（建设人力）可完全忽略
   • 道路信息只需读取边权（起点编号无用）

3. ​​时间复杂度​​：

   • O(n) 线性复杂度
   • 1秒可处理最大规模数据

测试点设计

​​测试类型​​	输入样例	预期输出	验证点
最小规模	n=1, B=[5], S=[3], 无边	0 3	单节点处理
边界值	n=10^5, 所有边权=10^4	2e9 ΣS_i	大数据溢出防护
维护人力不均	n=3, S=[100,200,300]	路径 600	人力累加正确性
道路权重差异	n=3, 边权=[1,1000]	2002 ΣS	路径计算正确性

优化建议

1. ​​I/O优化​​：

   ios::sync_with_stdio(false);
   cin.tie(0);

   禁用C与C++流同步，提升输入输出效率

2. ​​内存优化​​：

   • 不存储B数组，边权实时累加
   • 峰值内存仅需几KB

3. ​​算法扩展​​：

   • 若题目要求建设人力优化，需用树形DP：

   # 伪代码：树形DP求最小人力峰值
   def dfs(u, parent):
       dp[u] = S[u]  # 维护人力
       children = []
       for v in tree[u]:
           if v == parent: continue
           dfs(v, u)
           children.append((B[v]-S[v], dp[v]))
       # 贪心排序：净释放大的优先
       sort(children by B_v-S_v descending)
       
       current = 0  # 当前可用人力
       for (net_release, sub_dp) in children:
           if current < B[v]:
               dp[u] += B[v] - current  # 补充人力
               current = 0
           else:
               current -= B[v]
           current += net_release
           dp[u] += sub_dp - S[v]  # 累加子树需求