150. 逆波兰表达式求值--后缀表达式
力扣题目链接(opens new window)
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 + , - , * , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
- 输入: ["2", "1", "+", "3", " * "]
- 输出: 9
- 解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
逆波兰表达式:是一种后缀表达式,所谓后缀就是指运算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
-
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
-
适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中。
思路
递归就是用栈来实现的。所以栈与递归之间在某种程度上是可以转换的!
那么来看一下本题,其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点,按照后序遍历的规则画出一个二叉树。
但我们没有必要从二叉树的角度去解决这个问题,只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了,就可以了。
遇到运算符弹出栈顶两个元素进行运算,运算结果放回栈顶;遇到数字直接入栈。
题外话
我们习惯看到的表达式都是中缀表达式,因为符合我们的习惯,但是中缀表达式对于计算机来说就不是很友好了。
例如:4 + 13 / 5,这就是中缀表达式,计算机从左到右去扫描的话,扫到13,还要判断13后面是什么运算符,还要比较一下优先级,然后13还和后面的5做运算,做完运算之后,还要向前回退到 4 的位置,继续做加法,你说麻不麻烦!
那么将中缀表达式,转化为后缀表达式之后:["4", "13", "5", "/", "+"] ,就不一样了,计算机可以利用栈来顺序处理,不需要考虑优先级了。也不用回退了, 所以后缀表达式对计算机来说是非常友好的。
补充:java中的栈
Java中栈的实现方式对比
| 实现方式 | 所属包/类 | 线程安全 | 性能 | 功能特点 | 适用场景 | 不适用场景 |
|---|---|---|---|---|---|---|
Stack类 | java.util.Stack | 是(继承Vector) | 较差(同步开销) | 提供完整的栈操作(push/pop/peek),但继承了Vector的冗余方法 | 需要线程安全的简单栈操作 | 高并发或高性能场景 |
ArrayDeque | java.util.ArrayDeque | 否 | 最优(动态数组实现) | 实现了Deque接口,可模拟栈(push/pop)或队列 | 推荐:单线程环境下需要高性能的栈操作 | 需要线程安全的场景 |
LinkedList | java.util.LinkedList | 否 | 中等(链表节点开销) | 实现了Deque接口,支持栈操作(push/pop) | 需要频繁插入/删除或不确定容量时 | 需要快速随机访问的场景 |
| 自定义栈 | 自行实现(如基于数组或链表) | 取决于实现 | 可优化 | 完全控制内部逻辑和扩展性 | 需要特殊功能(如固定大小栈、最小栈等) | 追求开发效率时 |
使用stack类:
| 操作类型 | 方法 | 描述 | 返回值 | 异常 |
|---|---|---|---|---|
| 压栈操作 | E push(E item) | 将元素压入栈顶 | 被压入的元素 | - |
| 弹栈操作 | E pop() | 移除并返回栈顶元素 | 栈顶元素 | EmptyStackException(栈为空时) |
| 查看栈顶 | E peek() | 返回栈顶元素(不移除) | 栈顶元素 | EmptyStackException(栈为空时) |
| 检查空栈 | boolean empty() | 检查栈是否为空 | true(空栈)/false(非空) | - |
| 搜索元素 | int search(Object o) | 查找元素在栈中的位置(从栈顶开始计数,1为栈顶) | 元素位置(从1开始)/-1(未找到) | - |
| 获取大小 | int size() | 返回栈中元素数量 | 元素数量 | - |
| 获取元素 | E get(int index) | 获取指定索引处的元素(0为栈底,size()-1为栈顶) | 指定位置的元素 | IndexOutOfBoundsException(索引越界时) |
| 清空栈 | void clear() | 移除栈中所有元素 | - | - |
Java 中的 Deque 接口代表双向队列(Double-ended Queue),它允许在队列的两端(头部和尾部)高效地插入、删除和访问元素。
在 Java 中,Deque 和 ArrayDeque 是接口与实现类的关系,它们共同提供了双向队列(Double-ended Queue)的功能。
Deque 接口实现栈的方法对照表
定义:Deque<String> stack = new ArrayDeque<>();
| 栈操作 | Deque 方法 | 等效 Stack 类方法 | 功能描述 | 异常/返回值 |
|---|---|---|---|---|
| 压栈 (Push) | void push(E e) | E push(E item) | 将元素压入栈顶 | 失败时抛出 IllegalStateException(容量受限时) |
| 弹栈 (Pop) | E pop() | E pop() | 移除并返回栈顶元素 | 空栈时抛出 NoSuchElementException |
| 查看栈顶 (Peek) | E peek() | E peek() | 返回栈顶元素(不移除) | 空栈时返回 null |
| 检查空栈 | boolean isEmpty() | boolean empty() | 判断栈是否为空 | true(空栈)/false(非空) |
| 获取栈大小 | int size() | int size() | 返回栈中元素数量 | - |
Deque 的实现类对比
| 实现类 | 底层结构 | 线程安全 | 性能 | 适用场景 |
|---|---|---|---|---|
ArrayDeque | 动态数组 | 否 | 最优 | 默认选择(单线程高性能栈) |
LinkedList | 双向链表 | 否 | 中等 | 需要频繁增删或同时作为队列使用 |
用 Deque实现双向队列
Deque<String> stack = new ArrayDeque<>();
由于使用了 Deque 接口类型,它能调用所有双向队列的方法。以下是双向队列的核心操作总结:
双向队列操作总结表
| 操作类型 | 头部方法(First/Front) | 尾部方法(Last/Back) | 说明 |
|---|---|---|---|
| 插入元素 | addFirst(E e)offerFirst(E e) | addLast(E e)offerLast(E e) | 插入失败时: - addXXX() 抛出异常- offerXXX() 返回 false |
| 删除元素 | removeFirst()pollFirst() | removeLast()pollLast() | 队列为空时: - removeXXX() 抛出异常- pollXXX() 返回 null |
| 查看元素 | getFirst()peekFirst() | getLast()peekLast() | 队列为空时: - getXXX() 抛出异常- peekXXX() 返回 null |
| 栈操作(LIFO) | push(E e)(等价于 addFirst) | pop()(等价于 removeFirst) | 后进先出(栈的特性) |
| 队列操作(FIFO) | offer(E e)(等价于 offerLast) | poll()(等价于 pollFirst) | 先进先出(普通 |
class Solution {
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new ArrayDeque<>();
for(String s: tokens){
if("+".equals(s)){ // leetcode 内置jdk的问题,不能使用==判断字符串是否相等
stack.push( stack.pop() + stack.pop() );
}else if("-".equals(s)){
stack.push( -stack.pop() + stack.pop() );
}else if("*".equals(s)){
stack.push( stack.pop() * stack.pop() );
}else if("/".equals(s)){
int tmp1 = stack.pop();
int tmp2 = stack.pop();
stack.push(tmp2 / tmp1);
}else{ //数字直接入栈
stack.push(Integer.valueOf(s));
}
}
return stack.pop();
}
}#239. 滑动窗口最大值
力扣题目链接(opens new window)
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?

提示:
- 1 <= nums.length <= 10^5
- -10^4 <= nums[i] <= 10^4
- 1 <= k <= nums.length
思路
这是使用单调队列的经典题目。
不能使用优先级队列(大顶堆):底层使用二叉树,插入时自动排序,poll弹出时自动弹出最小值。
补充:java中的优先级队列
在 Java 里,优先级队列(PriorityQueue)的底层实现是最小堆(也被叫做二叉堆)。
- 插入操作(
offer):时间复杂度为 (O(log n))。在插入元素后,需要对堆进行调整,以维持堆的特性。 - 删除操作(
poll):时间复杂度同样是 \(O(\log n)\)。删除最小元素后,要重新调整堆结构。 - 查看操作(
peek):时间复杂度为 \(O(1)\),因为队列头部的元素就是最小元素。
下面是一个简单的代码示例,展示了 PriorityQueue 的基本用法:
import java.util.PriorityQueue;
import java.util.Comparator;
public class PriorityQueueExample {
public static void main(String[] args) {
// 自然顺序(最小堆)
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
minHeap.offer(3);
minHeap.offer(1);
minHeap.offer(2);
System.out.println(minHeap.poll()); // 输出: 1
// 自定义比较器(最大堆)
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
maxHeap.offer(3);
maxHeap.offer(1);
maxHeap.offer(2);
System.out.println(maxHeap.poll()); // 输出: 3
}
}所以需要自己DIY一种队列--单调队列!
作用:可以维护队列中的元素顺序,但是push、pop时还是弹出栈顶的元素,而不是排序后的元素
只维护可能成为最大值的元素
那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
大家此时应该陷入深思.....
其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。
那么这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列
不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。
来看一下单调队列如何维护队列里的元素。
动画如下:
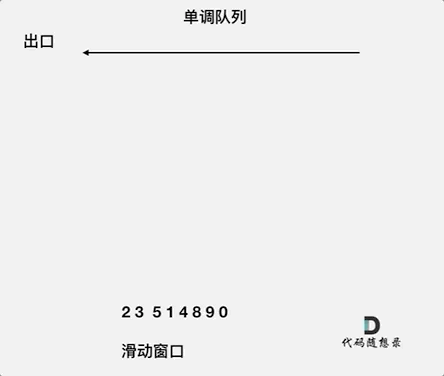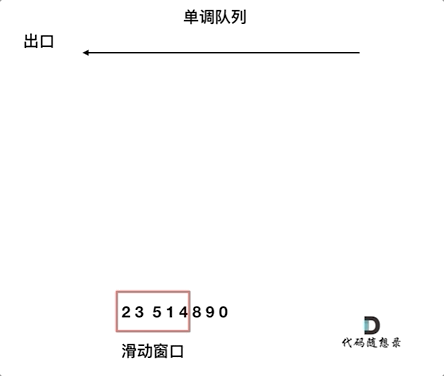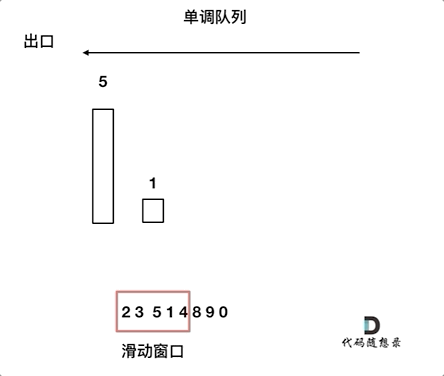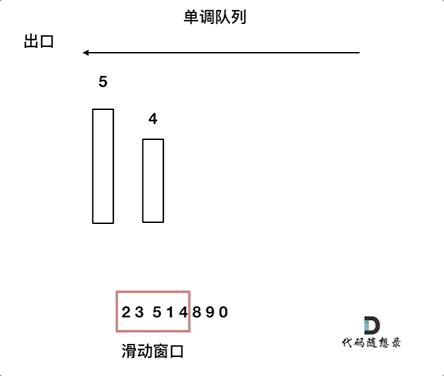
对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
- pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
- push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:
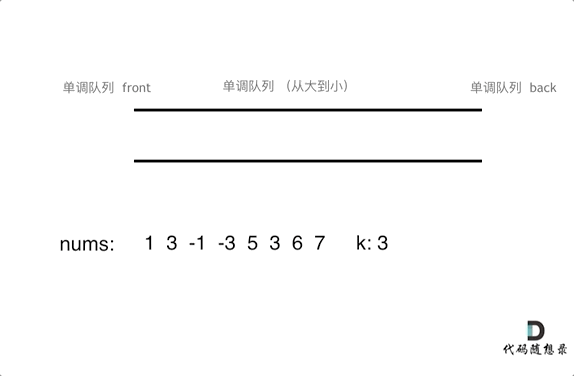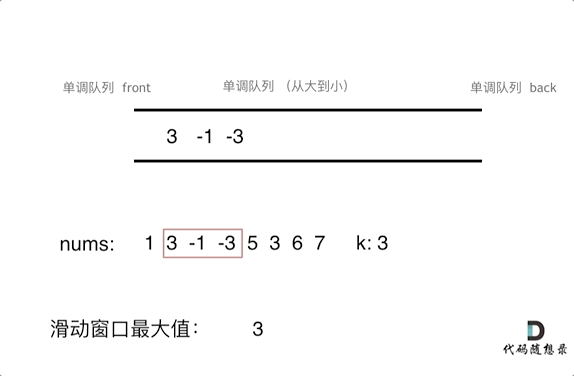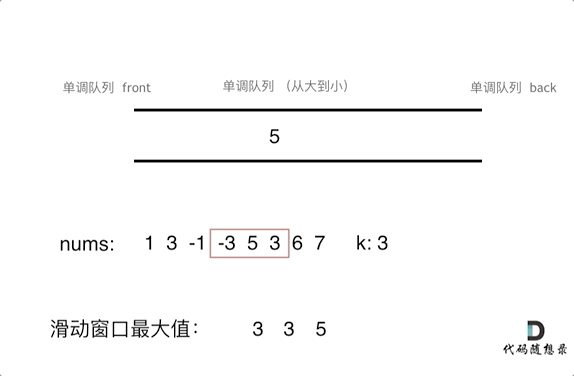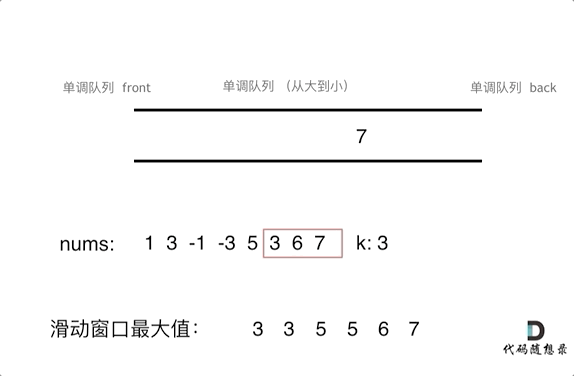
那么我们用什么数据结构来实现这个单调队列呢?
使用deque最为合适
错误第一版代码:
class Solution {
public static Deque<Integer> slidingWin = new ArrayDeque<>();
public int[] maxSlidingWindow(int[] nums, int k) {
if(k == 1 )return nums;
int res[] = new int[nums.length - k + 1];
for(int i = 0; i < k; i++){
pushthis(nums[i]);
}
for(int i = 0; i < nums.length - k + 1; i++){ //滑动过程
popfront(nums[i]);
pushthis(nums[i + k - 1]);
res[i] = getMaxVal();
}
return res;
}
private void popfront(int value){ //value是当前需要pop的值
if( !slidingWin.isEmpty() && value == getMaxVal()){ //只有在当前值是最大值时才弹出
slidingWin.pop();
}
}
private void pushthis(int value){ //value是当前需要push的值
while( !slidingWin.isEmpty() && slidingWin.peekLast() < value ){ //弹出双向队列后面所有比val小的值
slidingWin.pollLast();
}
slidingWin.offerLast(value);
}
private int getMaxVal(){ //获取当前窗口的最大值--即栈顶
return slidingWin.peekFirst();
}
}正确版本:
//解法一
//自定义数组
class MyQueue {
Deque<Integer> deque = new LinkedList<>();
//弹出元素时,比较当前要弹出的数值是否等于队列出口的数值,如果相等则弹出
//同时判断队列当前是否为空
void poll(int val) {
if (!deque.isEmpty() && val == deque.peek()) {
deque.poll();
}
}
//添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出
//保证队列元素单调递减
//比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
void add(int val) {
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
deque.add(val);
}
//队列队顶元素始终为最大值
int peek() {
return deque.peek();
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 1) {
return nums;
}
int len = nums.length - k + 1;
//存放结果元素的数组
int[] res = new int[len];
int num = 0;
//自定义队列
MyQueue myQueue = new MyQueue();
//先将前k的元素放入队列
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
//滑动窗口移除最前面的元素,移除是判断该元素是否放入队列
myQueue.poll(nums[i - k]);
//滑动窗口加入最后面的元素
myQueue.add(nums[i]);
//记录对应的最大值
res[num++] = myQueue.peek();
}
return res;
}
}
//解法二
//利用双端队列手动实现单调队列
/**
* 用一个单调队列来存储对应的下标,每当窗口滑动的时候,直接取队列的头部指针对应的值放入结果集即可
* 单调递减队列类似 (head -->) 3 --> 2 --> 1 --> 0 (--> tail) (左边为头结点,元素存的是下标)
*/
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
ArrayDeque<Integer> deque = new ArrayDeque<>();
int n = nums.length;
int[] res = new int[n - k + 1];
int idx = 0;
for(int i = 0; i < n; i++) {
// 根据题意,i为nums下标,是要在[i - k + 1, i] 中选到最大值,只需要保证两点
// 1.队列头结点需要在[i - k + 1, i]范围内,不符合则要弹出
while(!deque.isEmpty() && deque.peek() < i - k + 1){
deque.poll();
}
// 2.维护单调递减队列:新元素若大于队尾元素,则弹出队尾元素,直到满足单调性
while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
deque.offer(i);
// 因为单调,当i增长到符合第一个k范围的时候,每滑动一步都将队列头节点放入结果就行了
if(i >= k - 1){
res[idx++] = nums[deque.peek()];
}
}
return res;
}
}347.前 K 个高频元素
力扣题目链接(opens new window)
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
- 输入: nums = [1,1,1,2,2,3], k = 2
- 输出: [1,2]
示例 2:
- 输入: nums = [1], k = 1
- 输出: [1]
提示:
- 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
- 你的算法的时间复杂度必须优于 $O(n \log n)$ , n 是数组的大小。
- 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
- 你可以按任意顺序返回答案。
思路
这道题目主要涉及到如下三块内容:
- 要统计元素出现频率
- 对频率排序
- 找出前K个高频元素
首先统计元素出现的频率,这一类的问题可以使用map来进行统计。
然后是对频率进行排序,这里我们可以使用一种 容器适配器就是优先级队列。
大顶堆、小顶堆--适合求前k个结果
用大顶堆遍历一遍pop,剩下的是前K个低频元素。所以使用小顶堆
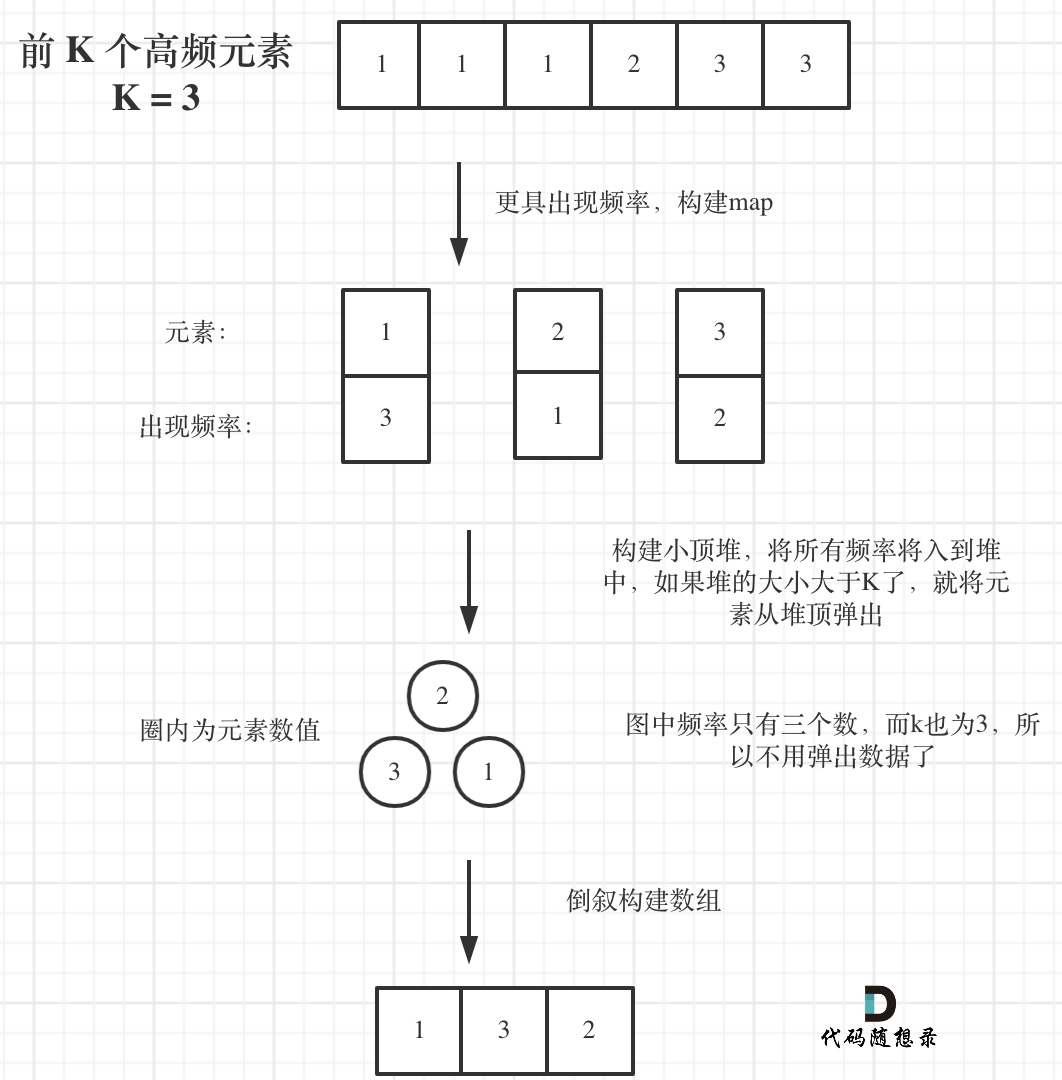
寻找前k个最大元素流程如图所示:(图中的频率只有三个,所以正好构成一个大小为3的小顶堆,如果频率更多一些,则用这个小顶堆进行扫描)
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 优先级队列,为了避免复杂 api 操作,pq 存储数组
// lambda 表达式设置优先级队列从大到小存储 o1 - o2 为从小到大,o2 - o1 反之
PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
int[] res = new int[k]; // 答案数组为 k 个元素
Map<Integer, Integer> map = new HashMap<>(); // 记录元素出现次数
for (int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
for (var x : map.entrySet()) { // entrySet 获取 k-v Set 集合
// 将 kv 转化成数组
int[] tmp = new int[2];
tmp[0] = x.getKey();
tmp[1] = x.getValue();
pq.offer(tmp);
// 下面的代码是根据小根堆实现的,我只保留优先队列的最后的k个,只要超出了k我就将最小的弹出,剩余的k个就是答案
if(pq.size() > k) {
pq.poll();
}
}
for (int i = 0; i < k; i++) {
res[i] = pq.poll()[0]; // 获取优先队列里的元素
}
return res;
}
}栈与队列总结篇
代码随想录
#栈与队列的理论基础
1. java中的stack和queue
Stack:Java 中有一个继承自Vector的具体类java.util.Stack(线程安全但性能较差,不推荐使用)。现代 Java 中更常用Deque接口(如ArrayDeque)来实现栈功能。Queue:Java 中的Queue是一个接口(继承自Collection),常见实现类有LinkedList、PriorityQueue等。
2.
| 特性 | Java 集合框架 | C++ STL |
|---|---|---|
| 核心机制 | 接口 + 实现类(面向对象) | 模板(泛型编程) |
| 线程安全 | 部分类线程安全(如 Vector) | 大部分非线程安全 |
| 栈实现 | Deque(推荐)或 Stack 类 | std::stack(适配器类) |
| 队列实现 | Queue 接口(如 LinkedList) | std::queue(适配器类) |
3. Java 中 Stack 和 Queue 的实现方式
栈(Stack)
- 传统实现:
java.util.Stack继承自Vector,内部使用动态数组存储元素,所有操作通过synchronized保证线程安全(但性能差)。 - 现代实现:推荐使用
Deque接口(如ArrayDeque或LinkedList),通过push()、pop()、peek()方法实现栈功能。ArrayDeque:基于动态数组,无容量限制,性能最优。LinkedList:基于双向链表,适合频繁插入 / 删除。
队列(Queue)
- 普通队列:
LinkedList(基于链表)或ArrayDeque(基于数组)。 - 优先队列:
PriorityQueue(基于最小堆)。 - 阻塞队列:
LinkedBlockingQueue、ArrayBlockingQueue等(用于并发编程)
4. stack,queue 提供迭代器来遍历空间么?
栈(Stack)
java.util.Stack:继承自Vector,支持iterator(),但遍历时顺序为 栈底到栈顶(与弹出顺序相反)。Deque实现的栈:iterator():从队首(栈底)到队尾(栈顶)。descendingIterator():从队尾(栈顶)到队首(栈底)。
队列(Queue)
- 普通队列:
iterator()按元素入队顺序遍历(FIFO)。 - 优先队列:
PriorityQueue的迭代器不保证元素的优先级顺序,仅用于快速遍历。
在C++中,可以出一道面试题:栈里面的元素在内存中是连续分布的么?
这个问题有两个陷阱:
- 陷阱1:栈是容器适配器,底层容器使用不同的容器,导致栈内数据在内存中不一定是连续分布的。
- 陷阱2:缺省情况下,默认底层容器是deque,那么deque在内存中的数据分布是什么样的呢? 答案是:不连续的,下文也会提到deque。
在java中,
ArrayDeque(基于动态数组)
-
内存分布:连续。
-
原理:
ArrayDeque内部使用动态数组存储元素,数组在内存中是连续分配的。
LinkedList(基于双向链表)
- 内存分布:不连续。
- 原理:
LinkedList由节点(Node)组成,每个节点包含元素值和指向前驱 / 后继节点的引用。节点在内存中是离散分配的,通过引用连接。
传统 java.util.Stack
- 内存分布:连续。
- 原理:
Stack继承自Vector,内部使用动态数组存储元素,因此内存连续。



















