1.摘要
本文针对肝癌(HCC)早期诊断难题,提出了一种基于改进成吉思汗鲨鱼优化算法(MGKSO)的计算机辅助诊断系统。由于HCC在早期症状不明显且涉及高维复杂数据,传统机器学习方法易受噪声和冗余特征干扰。为提升诊断准确性与效率,MGKSO融合了准对立学习(QOBL)与正交学习(OL)策略,有效增强了特征选择过程中的全局搜索与局部优化能力。

2.成吉思汗鲨鱼优化算法GKSO原理
【智能算法】成吉思汗鲨鱼优化算法(GKSO)原理及实现
3.MGKSO
MGKSO中引入了准对立学习(QOBL)机制,用来提升初始化阶段种群的多样性和全局搜索能力。在初始解生成过程中,每个候选解在给定的搜索边界内随机产生。在MGKSO中,QOBL通过计算解空间边界的平均值,生成位于搜索区域对侧的准对立解,提升搜索范围与解的多样性。为避免早期陷入局部最优,本研究将QOBL策略延后至初始化阶段末尾引入,从而更有效地推动算法向全局最优收敛。
x
j
O
B
L
=
L
B
j
+
U
B
j
−
x
j
x_j^{\mathrm{OBL}}=LB_j+UB_j-x_j
xjOBL=LBj+UBj−xj
x
j
Q
O
B
L
=
{
L
B
j
+
U
B
j
2
+
rand()
⋅
(
x
j
O
B
L
−
L
B
j
+
U
B
j
2
)
,
if
x
j
<
L
B
j
+
U
B
j
2
x
j
O
B
L
+
rand()
⋅
(
L
B
j
+
U
B
j
2
−
x
j
O
B
L
)
,
otherwise
x^{QOBL}_j = \begin{cases} \frac{LB_j + UB_j}{2} + \text{rand()} \cdot \left( x^{OBL}_j - \frac{LB_j + UB_j}{2} \right), & \text{if } x_j < \frac{LB_j + UB_j}{2} \\ x^{OBL}_j + \text{rand()} \cdot \left( \frac{LB_j + UB_j}{2} - x^{OBL}_j \right), & \text{otherwise} \end{cases}
xjQOBL=⎩
⎨
⎧2LBj+UBj+rand()⋅(xjOBL−2LBj+UBj),xjOBL+rand()⋅(2LBj+UBj−xjOBL),if xj<2LBj+UBjotherwise
在此之后,MGKSO开始使用布朗运动来模拟随机运动:
X
i
j
(
t
+
1
)
=
X
b
e
s
t
+
exp
(
(
t
i
t
)
4
)
×
(
R
B
−
0.5
)
×
(
X
b
e
s
t
−
Q
O
X
i
)
,
1
3
T
<
t
<
2
3
T
X_i^j(t+1) = X_{best} + \exp\left( \left( \frac{t}{it} \right)^4 \right) \times (RB - 0.5) \times (X_{best} - QOX_i), \quad \frac{1}{3}T < t < \frac{2}{3}T
Xij(t+1)=Xbest+exp((itt)4)×(RB−0.5)×(Xbest−QOXi),31T<t<32T
狩猎阶段:每个解
X
i
X_i
Xi会通过朝向当前已知的最优解移动来进行更新:
X
i
n
e
w
=
X
b
e
s
t
+
exp
(
i
t
e
r
M
a
x
i
t
e
r
)
4
⋅
(
R
i
−
0.5
)
⋅
(
X
b
e
s
t
−
X
i
)
X_i^{new}=X_{best}+\exp\left(\frac{iter}{Max_iter}\right)^4\cdot(R_i-0.5)\cdot(X_{best}-X_i)
Xinew=Xbest+exp(Maxiteriter)4⋅(Ri−0.5)⋅(Xbest−Xi)
最优解吸引:通过向最优解移动:
X
i
n
e
w
=
X
i
+
s
i
⋅
(
r
a
n
d
⋅
X
b
e
s
t
−
r
a
n
d
⋅
X
i
)
X_i^{new}=X_i+s_i\cdot \begin{pmatrix} rand\cdot X_{best}-rand\cdot X_i \end{pmatrix}
Xinew=Xi+si⋅(rand⋅Xbest−rand⋅Xi)
其中,
s
i
s_i
si是基于解的适应度的比例因子:
s
i
=
1.5
⋅
(
F
i
t
n
e
s
s
(
X
i
)
)
r
a
n
d
s_{i}=1.5\cdot\left(\mathrm{Fitness}(X_{i})\right)^{rand}
si=1.5⋅(Fitness(Xi))rand
觅食阶段:觅食阶段引入抛物线运动:
X
i
n
e
w
=
X
b
e
s
t
+
r
a
n
d
⋅
(
X
b
e
s
t
−
X
i
)
+
T
F
⋅
2
⋅
(
X
b
e
s
t
−
X
i
)
X_i^{new}=X_{best}+rand\cdot(X_{best}-X_i)+TF\cdotp^2\cdot(X_{best}-X_i)
Xinew=Xbest+rand⋅(Xbest−Xi)+TF⋅2⋅(Xbest−Xi)
自我保护机制:该机制通过引入复杂的扰动来保证多样性:
X
i
new
=
{
X
i
(
t
)
+
f
1
⋅
(
u
1
⋅
X
best
(
t
)
−
u
2
⋅
X
p
(
t
)
)
+
f
2
⋅
ρ
⋅
(
u
3
⋅
X
2
(
t
)
−
X
1
(
t
)
)
+
u
2
⋅
(
X
r
1
(
t
)
−
X
r
2
(
t
)
)
/
2
,
if
u
1
<
0.5
,
X
best
(
t
)
+
f
1
⋅
(
u
1
⋅
X
best
(
t
)
−
u
2
⋅
X
p
(
t
)
)
+
f
2
⋅
ρ
⋅
u
3
(
X
2
(
t
)
−
X
1
(
t
)
)
+
u
2
⋅
(
X
r
1
(
t
)
−
X
r
2
(
t
)
)
/
2
,
otherwise
.
X_i^{\text{new}} = \begin{cases} X_i(t) + f_1 \cdot \left( u_1 \cdot X_{\text{best}}(t) - u_2 \cdot X_p(t) \right) \\ \quad + f_2 \cdot \rho \cdot \left( u_3 \cdot X_2(t) - X_1(t) \right) \\ \quad + u_2 \cdot \left( X_{r1}(t) - X_{r2}(t) \right)/2, & \text{if } u_1 < 0.5, \\ X_{\text{best}}(t) + f_1 \cdot \left( u_1 \cdot X_{\text{best}}(t) - u_2 \cdot X_p(t) \right) \\ \quad + f_2 \cdot \rho \cdot u_3 \left( X_2(t) - X_1(t) \right) \\ \quad + u_2 \cdot \left( X_{r1}(t) - X_{r2}(t) \right)/2, & \text{otherwise}. \end{cases}
Xinew=⎩
⎨
⎧Xi(t)+f1⋅(u1⋅Xbest(t)−u2⋅Xp(t))+f2⋅ρ⋅(u3⋅X2(t)−X1(t))+u2⋅(Xr1(t)−Xr2(t))/2,Xbest(t)+f1⋅(u1⋅Xbest(t)−u2⋅Xp(t))+f2⋅ρ⋅u3(X2(t)−X1(t))+u2⋅(Xr1(t)−Xr2(t))/2,if u1<0.5,otherwise.
正交学习(OL)是一种广泛应用的技术,用来在通过在搜索过程中的探索和开发阶段之间实现平衡,从而增强对最优解的搜索能力。OL策略采用了正交实验设计(OED)方法,以构造出能有效代表群体的解,从而引导群体朝着全局最优解前进(Gao, Liu, & Huang, 2013)。通过在少量实验中确定因子水平的最佳组合,OED能够提供新的解,引导搜索过程更加高效地进行。OL策略分为两个主要阶段:
正交表(Orthogonal Array, OA):第一阶段涉及生成一个预定义的表格,称为正交表(OA),该表格由一系列特定的数字组成,通常表示为 L M ( L Q ) L_{M}(L^{Q}) LM(LQ)。

因子分析(FA):第二阶段使用成分分析,通过利用正交表(OA)中所有
M
M
M种可能组合的实验结果来实现,用于确定这种影响:
W
q
,
l
=
∑
m
=
1
M
f
(
C
m
)
⋅
E
m
,
q
,
l
W_{q,l}=\sum_{m=1}^Mf(C_m)\cdot E_{m,q,l}
Wq,l=m=1∑Mf(Cm)⋅Em,q,l
f
(
C
m
)
f(C_m)
f(Cm)表示正交表 (OA) 中第
m
m
m个组合的适应度。变量
E
m
,
q
,
l
E_{m,q,l}
Em,q,l在第
m
m
m个组合中,若第
q
q
q个因子使用的是第
l
l
l个水平,则设置为 1; 否则为 0。可以迅速确定每个水平对各因子的影响:
X
n
m
=
X
n
b
e
s
t
m
⊕
X
n
m
X_n^m=X_{n_{best}}^m\oplus X_n^m
Xnm=Xnbestm⊕Xnm
⊕ \oplus ⊕表示正交学习过程。

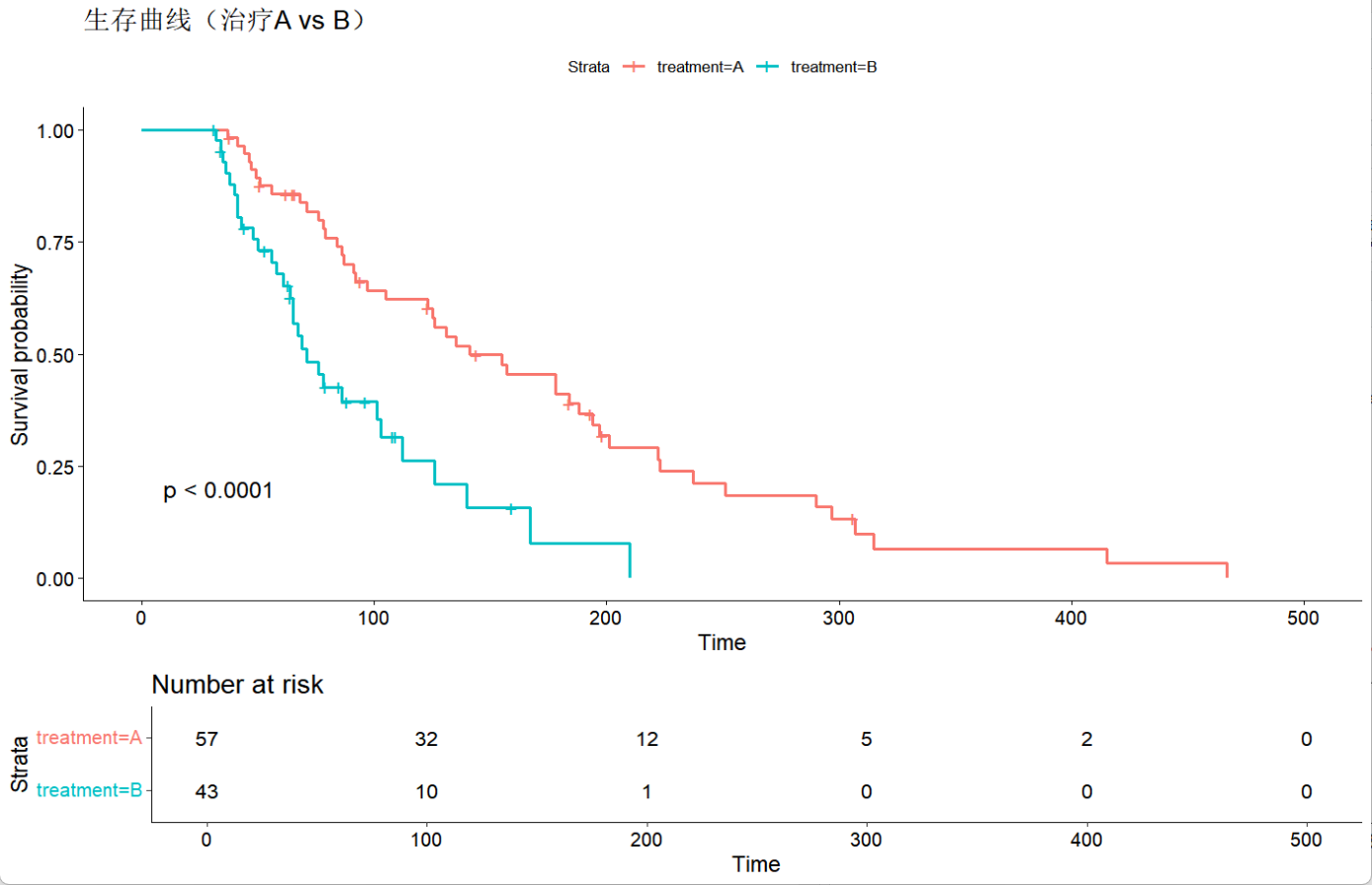
4.结果展示


5.参考文献
[1] Emam M M, Mostafa R R, Houssein E H. Computer-aided diagnosis system for predicting liver cancer disease using modified Genghis Khan Shark Optimizer algorithm[J]. Expert Systems with Applications, 2025, 285: 128017.