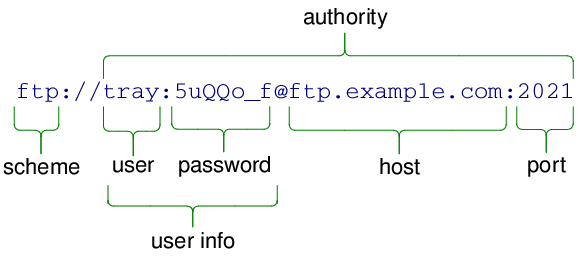
图论

题目

47. 参加科学大会（第六期模拟笔试）
改进版本的 dijkstra 算法（堆优化版本）
朴素版本的 dijkstra 算法解法的时间复杂度为 $O(n^2)$ 时间复杂度与 n 有关系，与边无关系
类似于 prim 对应点多的情况，kruskal 对应边多的情况
Djkstra 也可以着重于边，着重于边那么存储结构使用邻接表实现
优化的方法是：将边加入小顶堆中实现自动排序（最小边在堆顶），每次从堆顶取边即可
堆实现的三部曲，由于邻接表的存在不需要 for 循环遍历可能的边了，因此有如下代码
1. 第一步，选择原点到节点最近且未访问过的边，pair<节点编号，源点到该节点的权值>
我们不用 for 循环去遍历，直接取堆顶元素：
pair<int, int> cur = pq.Top (); pq.Pop ();
2. 第二步，选择最近节点标记访问过
Visited[cur. First] = true;
3. 第三步，更新非访问节点到原点距离（minDist 数组）
所以在邻接表中，我们要获取节点 cur 链接指向哪些节点，就是遍历 grid[cur 节点编号] 这个链表
cur.first 就是cur节点编号，参考上面pair的定义： pair<节点编号，源点到该节点的权值>
接下来就是更新非访问节点到源点的距离

// 3. 第三步，更新非访问节点到源点的距离（即更新minDist数组）
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点，cur指向的节点为 edge
    // cur指向的节点edge.to，这条边的权值为 edge.val
    if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
        minDist[edge.to] = minDist[cur.first] + edge.val;
        pq.push(pair<int, int>(edge.to, minDist[edge.to]));
    }
}

完整代码实现

#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <climits>

using namespace std;

// 小顶堆
class MyCmp {
public:
    bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
        return lhs.second > rhs.second;
    }
};

struct Edge {
    int to; // 邻接顶点
    int val; // 边权重
    Edge(int t, int w): to(t), val(w) {} // 构造函数
};

int main() {
    int n, m, x, y, val;
    cin >> n >> m;

    // 构造邻接表
    vector<list<Edge>> grid(n+1);
    vector<int> minDist(n+1, INT_MAX);
    vector<bool> vis(n+1, false);
    
    for (int i = 0; i < m; ++i) {
        cin >> x >> y >> val;
        grid[x].push_back(Edge(y, val));
    }

    int start = 1;
    int end = n;

    // 构造最小堆 存放pair<节点，节点到该节点的权值>
    // 参数1 存储元素类型 参数2 容器底层实现 参数3自定义比较函数
    priority_queue<pair<int, int>, vector<pair<int, int>>, MyCmp> pq;
    // 队列初始化为0
    pq.push(pair<int, int>(start, 0));
    minDist[start] = 0; // 起点距离0

    while (!pq.empty()) {
        // 1. 第一步选择原点到节点最近且未被访问过的点
        pair<int, int> cur = pq.top();
        pq.pop();

        if (vis[cur.first]) continue;
        
        // 2.标记访问过
        vis[cur.first] = true;

        // 3.更新非访问节点到原点距离
        for (Edge e : grid[cur.first]) {
            // 获得当前节点指向的节点
            // cur指向节点e.to 边权值未e.val
            if (!vis[e.to] && minDist[cur.first] + e.val < minDist[e.to]) {
                minDist[e.to] = minDist[cur.first] + e.val;
                pq.push(pair<int, int>(e.to, minDist[e.to]));
            }
        }
    }

    if (minDist[end] == INT_MAX) cout << -1 << endl;
    else cout << minDist[end] << endl;
}

94. 城市间货物运输 I
Bellman_ford 算法介绍，本体不同于上面 dijkstra，此时的权重存在负数
Bellman_ford算法的核心思想是对所有边进行松弛n-1次操作（n为节点数量）从而求得目标最短路
不断尝试更新所有的边，直到所有可能的路径都被找到
什么是松弛？举个例子
每条边有起点、终点和边的权值。例如一条边，节点A 到节点B 权值为value，如图：
minDist[B] 表示 到达B节点 最小权值，minDist[B] 有哪些状态可以推出来？
状态一： minDist[A] + value 可以推出minDist[B]
状态二： minDist[B] 本身就有权值 （可能是其他边链接的节点B 例如节点C，以至于 minDist[B] 记录了其他边到 minDist[B] 的权值）如何确定 minDist[B]？
本题我们要求最小权值，那么 这两个状态我们就取最小的
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
也就是说，如果通过 A 到 B 这条边可以获得更短的到达B节点的路径，即如果 minDist[B] > minDist[A] + value，那么我们就更新 minDist[B] = minDist[A] + value 这个过程就叫做 “松弛”
以上讲了这么多，其实都是围绕以下这句代码展开：这句代码就是 Bellman_ford算法的核心操作。
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
也可以这样写
minDist[B] = min(minDist[A] + value, minDist[B])
其实 Bellman_ford算法也是采用了动态规划的思想，即：将一个问题分解成多个决策阶段，通过状态之间的递归关系最后计算出全局最优解。
那么为什么是 n - 1次松弛呢？这里要给大家模拟一遍 Bellman_ford 的算法才行，接下来我们来看看对所有边松弛 n - 1 次的操作是什么样的。
模拟过程
初始化过程。起点为节点1，起点到起点的距离为0，所以 minDist[1] 初始化为0

其他节点对应的minDist初始化为max，因为我们要求最小距离，那么还没有计算过的节点默认是一个最大数，这样才能更新最小距离。对所有边进行第一次松弛。
接下来我们来松弛一遍所有的边。边：节点5 -> 节点6，权值为-2 ，minDist[5] 还是默认数值max，所以不能基于节点5 去更新节点6

边：节点1 -> 节点2，权值为1 ，minDist[2] > minDist[1] + 1 ，更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1

边：节点5 -> 节点3，权值为1 ，minDist[5] 还是默认数值max，所以不能基于节点5去更新节点3

边：节点2 -> 节点5，权值为2 ，minDist[5] > minDist[2] + 2 （经过上面的计算minDist[2]已经不是默认值，而是 1），更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3

边：节点2 -> 节点4，权值为-3 ，minDist[4] > minDist[2] + (-3)，更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2

边：节点4 -> 节点6，权值为4 ，minDist[6] > minDist[4] + 4，更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2

边：节点1 -> 节点3，权值为5 ，minDist[3] > minDist[1] + 5 更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5

以上是对所有边进行一次松弛之后的结果。
那么需要对所有边松弛几次才能得到 起点（节点1） 到终点（节点6）的最短距离呢？
对所有边松弛一次，相当于计算起点到达与起点一条边相连的节点的最短距离。
注意我上面讲的是 对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离，这里 说的是 一条边相连的节点。
与起点（节点1）一条边相邻的节点，到达节点2 最短距离是 1，到达节点3 最短距离是5。
而 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 是 与起点 三条边相连的路线了。
所以对所有边松弛一次 能得到 与起点 一条边相连的节点最短距离。
那对所有边松弛两次 可以得到与起点 两条边相连的节点的最短距离。
那对所有边松弛三次 可以得到与起点 三条边相连的节点的最短距离，这个时候，我们就能得到到达节点3真正的最短距离，也就是 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线。
那么再回归刚刚的问题，需要对所有边松弛几次才能得到 起点（节点1） 到终点（节点6）的最短距离呢？节点数量为n，那么起点到终点，最多是 n-1 条边相连。
那么无论图是什么样的，边是什么样的顺序，我们对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
其实也同时计算出了，起点到达所有节点的最短距离，因为所有节点与起点连接的边数最多也就是 n-1 条边。

#include <iostream>
#include <vector>
#include <list>
#include <climits>

using namespace std;

int main() {
    int n, m, x, y, val;
    cin >> n >> m;

    // 使用朴素存储图
    vector<vector<int>> grid;
    for (int i = 0; i < m; ++i) {
        cin >> x >> y >> val;
        grid.push_back({x, y, val});
    }

    int start = 1;
    int end = n;

    vector<int> minDist(n+1, INT_MAX);
    minDist[start] = 0;

    // 对所有边松弛n-1次
    for (int i = 1; i < n; ++i) {
        // 每一次松弛是对所有边松弛
        for (vector<int>& side : grid) {
            int from = side[0];
            int to = side[1];
            int price = side[2];

            // 松弛操作
            if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
                minDist[to] = minDist[from] + price;
            }
        }
    }
    if (minDist[end] == INT_MAX) cout << "unconnected" << endl;
    else cout << minDist[end] << endl;

    return 0;
}