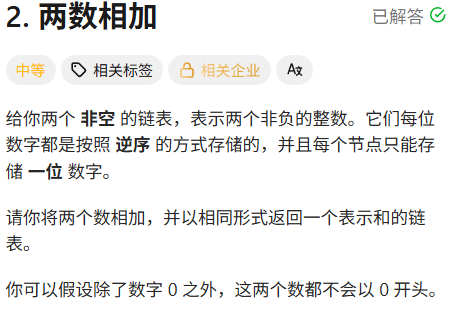

解答:
方法一:迭代
迭代大致过程就是:
算两条链表的当前位的和,加上上一位留下来的进位,就是新链表的当前位的数字。计算当前的进位。
这样,我们迭代需要的东西是:链表1,链表2,进位。故有addTwoNumbers(ListNode* l1, ListNode* l2,int carry=0)
迭代结束条件分析:链表1到空,链表2到空,进位是0
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2,int carry=0) {
//递归法,carry代表要进的位
if(l1==nullptr&&l2==nullptr&&carry==0){
return nullptr;
}
int s=carry;//记录当前数位的数字
if(l1){
s+=l1->val;
l1=l1->next;
}
if(l2){
s+=l2->val;
l2=l2->next;
}
return new ListNode(s%10,addTwoNumbers(l1,l2,s/10));
}
};
n,m代表两条链表的长度
时间复杂度:O(max(n,m))
空间复杂度:O(max(n,m))
方法二:迭代
哨兵节点是不是日记29link也见过!
这里注意初始化新的节点写法new ListNode();还要注意创建了哨兵节点以后,需要ListNode* cur=&dummy;来指向哨兵节点,再继续添加新节点哦!
返回的时候要返回dummy->next哦!因为dummy本身是空的。
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode dummy;
ListNode* cur=&dummy;
int carry=0;//进位
while(l1||l2||carry){//如果链表没有都遍历到最后,或者进位不是0,就一直迭代下去
if(l1){
carry+=l1->val;
l1=l1->next;
}
if(l2){
carry+=l2->val;
l2=l2->next;
}
cur=cur->next=new ListNode(carry%10);
carry/=10;
}
return dummy.next;
}
};
时间复杂度:O(max(n,m))
空间复杂度:O(1)
空间复杂度详解
递归法:
递归调用深度:每次递归处理两个链表的一个节点,直到两个链表均遍历完成且无进位。递归深度等于较长链表的长度(假设为L)加上可能的额外一位进位。
例如:
输入链表长度分别为m和n,则递归深度为max(m, n) + 1。
最坏情况下(如两个相同长度的链表全为9且相加后连续进位),递归深度等于链表长度。
栈空间开销:每次递归调用需在栈中保存局部变量(l1、l2、s等)及返回地址。总栈空间需求与递归深度成正比。
结果链表空间:虽然递归过程中创建了结果链表节点,但通常将输出结果视为算法的必要输出,不计入"额外空间"复杂度(但若需统计所有空间,则应考虑结果链表占用的O(L)空间)。
最终空间复杂度:O(max(m, n)),其中m和n分别为输入链表的长度。这是由于递归调用栈的最大深度与链表长度成线性关系。
空间复杂度的定义:
空间复杂度(Space Complexity)是指算法在运行过程中临时占用的内存空间的大小。
它包括所有局部变量、参数以及递归调用栈所占用的空间。
在递归算法中,由于每次递归调用都会创建新的栈帧,因此递归深度是影响空间复杂度的关键因素。
迭代法
所以在迭代法中,新建立的链表的节点是结果的一部分,不是临时占用的内存空间,不计入空间复杂度,只有常量级别的额外空间。