目录
第 4 章 栈、队列和数组
4.1 栈
4.1.1 栈的基本概念
4.1.2 栈的基本操作
4.1.3 栈的实现
1.顺序栈
2.链式栈
3.共享栈
4.1.4 顺序栈的基本操作实现
1.初始化栈
2.判空
3.判满
4.元素进栈
5.元素出栈
6.获取栈顶元素
4.1.5 链栈的基本操作实现
1.元素进栈
2.元素出栈
4.1.6 习题精编
4.1.7 真题演练
4.2 队列
4.2.1 队列的基本概念
4.2.2队列的基本操作
4.2.3队列的两种实现
1.顺序队列
2.链式队列
4.2.4循环队列的基本操作实现
1.初始化队列
编辑2.循环队列判空
3.循环队列判满
4.元素入队
5.元素出队
4.2.5 链式队列的基本操作实现
1.初始化队列
2.链式队列判空
3.元素入队
4.元素出队
4.2.6 双端队列
4.2.7 习题精编
4.2.8 真题演练
4.3 栈与队列的应用
4.3.1 栈在括号匹配中的应用
4.3.2 栈在表达式求值中的应用
1.基本概念
2.中缀表达式转为后缀表达式
3.后缀表达式的求值
4.前缀表达式
5. 栈在递归中的应用
4.3.3 习题精编
4.3.4 真题演练
4.4 数组与矩阵压缩存储
4.4.1 数组的基本概念
1.一维数组
2.多维数组
4.4.2 特殊矩阵的压缩存储
1.对称矩阵
2.上 / 下三角矩阵
3.稀疏矩阵
2.三对角矩阵
4.4.3 习题精编
4.4.4 真题演练
4.5 章末总结
第 4 章 栈、队列和数组
【考纲内容】
1.栈和队列的基本概念
2.栈和队列的顺序存储结构
3.栈和队列的链式存储结构
4.多维数组的存储
5.特殊矩阵的压缩存储
6.栈、队列和数组的应用
【考情统计】
年份
题数及分值
考点
单选题
综合题
总分值
2009
2
0
4
栈和队列的出入操作、队列的应用
2010
2
0
4
栈和队列的出入操作
2011
2
0
4
栈的出入操作、循环队列判空
2012
1
0
2
栈在后缀表达式中的应用
2013
1
0
2
栈的出入操作
2014
2
0
4
栈在后缀表达式中的应用、循环队列判空判满
2015
1
0
2
栈在递归中的应用
2016
2
0
4
队列的出入操作、三对角矩阵的压缩存储
2017
2
0
4
栈综合、稀疏矩阵的压缩存储
2018
3
0
6
栈与队列的出入操作、对称矩阵的压缩存储
2019
0
1
10
队列设计
2020
2
0
4
三角矩阵的压缩存储、栈的出入操作
2021
2
0
4
输出受限的双端队列、二维数组的存储
2022
1
0
2
栈的出入操作
2023
1
0
2
稀疏矩阵存储
2024
1
0
2
中缀表达式转化为等价的后缀表达式
【考点解读】
本章内容可以理解为线性表的应用。栈和队列是线性表的子集(和线性表一样具有顺序结构和链式结构),是操作受限的线性表。在复习中要熟悉栈和队列的逻辑结构,掌握元素出入过程、栈和队列的判空判满条件等,同时要掌握栈与队列的常见应用。
【复习建议】
复习时需要重点掌握:
1.栈与队列出人过程的模拟,各类栈与队列的判空判满条件。
2.栈在表达式求值中的运用,尤其是中缀表达式转后缀表达式的过程。
3.矩阵压缩存储的下标计算方法。
4.1 栈
4.1.1 栈的基本概念
栈(Stack)是一种只能从一端进行数据插入或删除且遵循后进先出(LIFO,Last - In - First - Out)(也称为:先进后出(FILO,First - In - Last - Out))原则的线性表。即后进栈(或称为入栈)的元素反而先出栈。执行数据插入和删除操作的一端被称为栈顶,另一端被称为栈底。栈的操作都是在栈顶进行的。栈的示意图如图 4.1 所示。
可以把栈类比成摞起来的餐盘:当取一个餐盘时,从一摞餐盘的顶部取走一个;当放回餐盘的时候,则依旧放在这一摞的顶部。
一个入栈与出栈的实例如图 4.2 所示:初始时为空栈,元素 1、2 依次入栈,2 出栈,3 入栈,之后 3、1 依次出栈,最终得到空栈。
1.栈的特点是 (1),队列的特点是 (2),栈和队列都是 (3)。若进栈序列为 1234,则 (4) 不可能是一个出栈序列(不一定全部进栈后再出栈);若进队列的序列为 1234,则 (5) 是一个出队序列。
(1) A. 先进先出
B. 后进先出
C. 进优于出
D. 出优于进
(2) A. 先进先出
B. 后进先出
C. 进优于出
D. 出优于进
(3) A. 顺序存储的线性结构
B. 链式存储的线性结构
C. 限制存取点的线性结构
D. 限制存取点的非线性结构
(4) A. 4231
B. 1324
C. 3241
D. 3214
(5) A. 4231
B. 1234
C. 3241
D. 32141.【参考答案】B、A、C、A、B
【解析】这题是一道基础概念题,栈的特点是后进先出,队列的特点是先进先出,栈和队列都是限制存取点的线性结构。对于 1234 进栈,可由 IOIIOOIO 得 1324,IIIOOIOO 得 3241,IIIOOOIO 得 3214。4.1.2 栈的基本操作
栈也是线性表,其特殊性在于栈的基本操作是线性表操作的子集,栈是操作受限的线性表。栈的基本操作如下:
// 1. 初始化,构造一个空栈 void initialize(Stack &S); // 2. 插入元素,也称入栈或进栈,在S的栈顶插入新的元素e bool push(Stack &S, ElemType e); // 3. 删除元素,也称出栈,获取S的栈顶元素e,并删除 ElemType pop(Stack &S); // 4. 获取栈顶元素,但不删除 ElemType getTop(Stack S); // 5. 判空,判断S是否为空栈 bool stackEmpty(Stack S);在以上的基本操作中,只有进栈和出栈会改变栈内元素。因为只需要对栈顶元素进行操作,所以用栈顶指针 top 来标识栈顶元素所在位置。如图 4.3 所示,栈是只能在 top 位置进行插入和删除的线性表。
注意:栈顶指针不一定是指针,对于顺序存储的栈,可使用数组下标作为栈顶指针。
【例 4.1】将 a、b、c 按次序入栈(不一定连续入栈),下面不可能为出栈序列的是( )。
A. a、b、c
B. c、a、b
C. b、c、a
D. c、b、a解析:选 B,因 c 后 a,b 非倒序。如果操作次序为 a 入栈、a 出栈、b 入栈、b 出栈、c 入栈、c 出栈,则出栈序列为 a、b、c,排除 A。如果操作次序为 a 入栈、b 入栈、b 出栈、c 入栈、c 出栈、a 出栈,则出栈序列为 b、c、a,排除 C。如果操作次序为 a 入栈、b 入栈、c 入栈、c 出栈、b 出栈、a 出栈,则出栈序列为 c、b、a,排除 D。所有合法的出栈序列个数为 1/(3 + 1)×C₆³ = 5 个(见章末总结的卡特兰数 (第 108 页)),剩下两个合法的出栈序列为 a、c、b 和 b、a、c。
4.1.3 栈的实现
栈的实现方式与线性表十分类似,只是在线性表的基本操作上施加一些限制。
1.顺序栈
采用顺序存储结构的栈称为顺序栈,它将栈底到栈顶的数据元素存放在一组地址连续的存储单元中,并采用 top 变量作为栈顶指针。顺序栈的结构定义如下:
#define MAX_SIZE 100 typedef struct { ElemType data[MAX_SIZE]; // 存放栈中具体元素 int top; // 指向栈顶位置 } SqStack;
对于顺序栈,还可以实现判满(stackFull)的操作:当 top 指针指向 MAX_SIZE - 1 的位置(即图中的 n - 1),栈就是一个满栈。
2.链式栈
采用链式存储结构的栈被称为链栈,又称链式栈。链栈基于链表实现,可以采取头插法或尾插法,选择链表的任意一端作为栈的栈顶。如果采用头插法,可以用链表的头指针 L(对于栈,用指针 S 代替)作为栈顶指针(无头结点的情况);而如果采用尾插法,则需要用链表的尾指针 rear 来作为栈的栈顶指针。
图 4.5 给出的是采用头插法与尾插法依次插入 a₀、a₁、a₂的链栈。其中在图 4.5 (b) 中使用了双向链表,这是因为使用尾插法出栈时需要能访问前驱结点,例如移出 a₂时 top 指针应指向 a₁。
链栈的空间可以动态申请,因此无需进行栈满的判断。
链栈(头插法)结构定义代码如下:typedef struct StackNode { // 链栈的结点 ElemType data; struct StackNode *next; } StackNode, *LinkStack;【例 4.2】栈是( )。
A. 顺序存储的线性结构
B. 限制存取点的线性结构
C. 链式存储的非线性结构
D. 限制存取点的非线性结构解析:选 B,顺序存储和链式存储是指物理结构。栈是只允许在一端进行插入或删除操作的线性结构,而且栈既可以顺序存储也可以链式存储,所以单说哪一种都是不够准确的。
3.共享栈
如图 4.6 所示,有时还可以将两个栈放在同一段存储空间中,分别让两个栈从两端开始往中间增长,这种栈被称为共享栈。
对一个满栈继续执行进栈操作,会导致上溢;对一个空栈继续执行出栈操作,会导致下溢。栈往往不止一个,如果给每个栈分配很大的空间来解决上溢的问题,将会造成存储空间的浪费。因此采用共享栈能在节省存储空间的基础上,在一定程度上避免上溢。
4.1.4 顺序栈的基本操作实现
顺序栈中各基本操作的实现可与上一章顺序表的基本操作进行对比学习。
1.初始化栈
void initialize(SqStack &S) { S.top = -1; // 初始化栈顶指针 } SqStack S; initialize(S);2.判空
栈空条件:对于顺序栈,当 top 等于 - 1 时为空栈(也可以设置 top 为 0 时表示空栈,相当于 top 指向栈顶元素的下一个位置);对于链式栈,当 top 所指元素为 NULL 时为空栈。
bool stackEmpty(SqStack S) { return S.top == -1; }3.判满
当 top 指针等于 MAX_SIZE - 1 的位置,栈就是一个满栈。
bool stackFull(SqStack S) { return S.top == MAX_SIZE - 1; }思考:共享栈的判空和判满应该如何表示?(答案在本节习题中)
4.元素进栈
如图 4.7 所示,元素进栈时先将 top 指针进行加一操作后再将元素插入。
bool push(SqStack &S, ElemType e) { if (stackFull(S)) // 若栈满则插入失败 return false; S.top++; // 将栈顶指针后移 S.data[S.top] = e; // 插入元素 return true; }注意:在栈初始化时也可让 top = MAX_SIZE,每次插入元素时,top 向低地址方向移动,即 “栈从高地址向低地址增长”。进程在虚拟地址空间中所拥有的栈区就是从高地址向低地址增长。
1.有一个空栈,栈顶指针为 3000H,每个元素需要一个存储单元,执行 Push、Push、Push、Push、Pop、Push、Pop、Push 操作后,栈顶指针的值为( )。
A. 3002H
B. 3003H
C. 3004H
D. 3005H1.【参考答案】 C
【解析】 共六次Push,两次Pop,所以栈中增加了四个元素,3000H + 4H = 3004H。5.元素出栈
ElemType pop(SqStack &S) { // 空栈不能弹出元素,操作错误,用宏定义ERROR表示错误 if (stackEmpty(S)) { return ERROR; } ElemType e = S.data[S.top]; // 拷贝元素 S.top--; // 将栈顶指针前移 return e; }如图 4.8 所示,模拟元素的出栈过程。注意此处和顺序表相同,出栈的元素还保留在原本的存储单元中,但在逻辑上已经无法访问了。
6.获取栈顶元素
bool getTop(SqStack S, ElemType &e) { if (stackEmpty(S)) return false; e = S.data[S.top]; // 拷贝元素 return true; }思考:如果让栈顶指针指向当前栈顶元素的下一个位置,空栈时的 top 值应该是多少?上面的操作顺序需要在哪些地方做出改变(先动指针还是先赋值)?(答案在本节习题中)
4.1.5 链栈的基本操作实现
对于链式栈,此处给出插入和删除操作的实现,以无头结点并采用头插法的链表进行介绍。元素进栈与出栈各步操作的示意图可参考线性表相关章节。
1.元素进栈
bool push(LinkStack& S, ElemType e) { StackNode *top = S; // 栈顶指针 StackNode *q = (StackNode*)malloc(sizeof(StackNode)); if (q == NULL) // 分配空间失败 return false; q->data = e; q->next = top; // 插入元素 S = q; // 将栈顶指针指向插入元素 return true; }2.元素出栈
ElemType pop(LinkStack &S) { if (stackEmpty(S)) { return ERROR; } StackNode *top = S; // 栈顶指针 ElemType e = top->data; // 取出栈顶元素 S = top->next; // 将栈顶指针指向后一个元素 free(top); return e; }对于尾插法、采用头结点的链表等其他情况,考生可以尝试思考完成。
提示:本节的重点在于理解栈中元素的出入过程,以及栈顶指针 top 的变化。
【例 4.3】假定顺序栈使用数组 a [n] 表示,top 表示栈顶指针,top == -1 时为空栈,并已知栈未满,当元素 x 进栈时所执行的操作为( )。
A. a [top -- ] = x
B. a [ -- top] = x
C. a [ ++ top] = x
D. a [top ++ ] = x解析:选 C,top++ 和 ++top 都属于自增运算,区别是对变量 top 的值进行自增的时机不同。top++ 是先进行取值,后进行自增。++top 是先进行自增,后进行取值。初始时 top 为 - 1,则第一个元素入栈后,top 为 0,即指向栈顶元素,故入栈是应先将指针 top 加 1,再将元素入栈,所以 C 正确。
4.1.6 习题精编
1.有一个空栈,栈顶指针为 3000H,每个元素需要一个存储单元,执行 Push、Push、Push、Push、Pop、Push、Pop、Push 操作后,栈顶指针的值为( )。
A. 3002H
B. 3003H
C. 3004H
D. 3005H1.【参考答案】 C
【解析】 共六次Push,两次Pop,所以栈中增加了四个元素,3000H + 4H = 3004H。2.设 a,b,c,d,e,f 按照顺序进栈,允许随时出栈,则不可能的出栈操作是( )。
A. bca fed
B. fedcba
C. cbadef
D. cadbef2.【参考答案】 D
【解析】 对于D选项,注意到c和a连续出栈而b不出栈是无法实现的。假设I是入栈操作,O是出栈操作,A可由IIOIOOIIIIOOO得到,B可由IIIIIIOOO0000得到,C可由IIIIOOOIOIOIO得到。3.用 I 表示进栈,O 表示出栈,则 abed 顺序进栈,允许随时出栈,得到出栈序列 bcad 的相应的操作是( )。
A. IIOIOOIO
B. IOIOIIOO
C. IIIOOIOO
D. IOIIOOIO3.【参考答案】 A
【解析】 只需要按照选项所给进行模拟即可得出答案,B的出栈序列是abdc,C的出栈序列是cbda,D的出栈序列是aebd。4.设栈的输入序列是 1,2,3,4,则不可能是其出栈序列的是( )。
A. 1243
B. 2134
C. 1432
D. 43124.【参考答案】 D
【解析】 对于4312,4第一个出栈说明4出栈时123都在栈内,并顺序排列,因为若不是顺序排列说明前面已经有元素输出,那第一个元素就不会是4,则出栈顺序不可能是312。5.设 n 个元素的进栈序列是 1,2,3,…,n,其输出序列是 p₁,p₂,p₃,…,pₙ,若 p₁ = 3,则 p₂的值为( )。
A. 一定是 2
B. 一定是 1
C. 不可能是 1
D. 以上都不对5.【参考答案】 C
【解析】 同上,当p₁ = 3时说明3出栈时12都在栈内并顺序排列,因为若不是顺序排列说明前面已经有元素输出,那第一个元素就不会是3,因此p₂不可能是1。6.(多选) 若一个栈的入栈序列为 1,2,3,4,其出栈序列为 p₁,p₂,p₃,p₄,则 p₂和 p₄可能为( )。
A. 2,4
B. 2,1
C. 4,3
D. 3,46.【参考答案】 A、B、D
【解析】 可以经过出入栈模拟得到所有可能的出入栈序列,进而选出答案。假设I是入栈操作,O是出栈操作,则A是IOIOIOIO,B是IIIIOOIOO,D是IOIIOOIO。对于C,若p₂为4,则说明在第二次出栈操作时1234已全部进栈,且123其中一个已经在p₁位置出栈,若p₁为3,此时为IIIIOIO不符合题意,若p₁为1(即IOIIIO)或2(即IIOIOIIO),则当4在p₂位置出栈后,栈顶元素一定为3,因此p₃为3,p₄不可能为3。7.(多选) 共享栈的好处是( )。
A. 减少存取时间
B. 节省存储空间
C. 降低上溢的可能
D. 降低下溢的可能7.【参考答案】 B、C
【解析】 上溢就是缓冲器满,还往里写;下溢就是缓冲器空,还往外读。为了解决上溢,可以给栈分配很大的空间,而这样又会造成空间的浪费,共享栈的提出就是为了在解决上溢的基础上节省存储空间,将两个栈放在同一段更大的空间内。共享栈和普通栈的存取时间都是O(1),因此不会减少存取时间。8.一个栈的输入序列为 1,2,3,⋯,n,若输出序列的第一个元素是 n,输出的第 i (1≤i≤n) 个元素是( )。
A. 不确定
B. n - i
C. i
D. n - i + 18.【参考答案】 D
【解析】 首先第一个输出元素为n说明栈中元素顺序排列,所以输出的第二个元素是n - 1,第三个元素是n - 2,以此类推,输出的第i个元素为n - i + 1。选D。9.若进栈序列为 1,2,3,4,5,可能得到的出栈序列是( )。
A. 12534
B. 31254
C. 32541
D. 142359.【参考答案】 C
【解析】 假设I是入栈操作,O是出栈操作,C可由IIIIOOIIOOO得到。10.对于空栈时 top == 0 的栈,进栈操作的操作顺序是( ),出栈操作的操作顺序是( )。
①判断栈是否为空栈;②判断栈是否为满栈;③top 自增;④top 自减;⑤插入或删除
A. ①⑤④
B. ②③⑤
C. ②⑤③
D. ①④⑤10.【参考答案】 C、D
【解析】 对于空栈时top == 0的栈,top指针指向栈顶元素的下一个,因此进栈时先进后自增,出栈时先自减后出栈。11.一个栈的输入序列为 1,2,3,⋯,n,若存在 k > 1 使第 k 个输出的元素为 n,则输出的第 i (i> k) 个元素是( )。
A. 不确定
B. n - i - k
C. n - i + k
D. n - i + 111.【参考答案】 A
【解析】 相比于之前知道n是第一个输出,若n在中间输出,则往后的出栈序列无法确定,因为任意一个元素都可以在入栈后立即出栈,作为第一个出栈的元素。12.有六个元素 6,5,4,3,2,1 的顺序进栈,则下列不是合法出栈序列的是( )。
A. 543612
B. 453126
C. 346521
D. 23415612.【参考答案】 C
【解析】 A可由IIOIOIOIOOIIOO得到。B可由IIIIOOIOIIOOO得到。C可由IIIIOO得到34,此时栈顶元素是5,无法直接将6出栈,故C错误。D可由IIIIIIOOOIOOO得到。13.C 语言标识符的第一个字符不能是数字,当字符序列 “t3_” 作为栈的输入时,输出长度为 3,且可用做 C 语言标识符的序列有( )个。
A. 4
B. 5
C. 6
D. 313.【参考答案】 D
【解析】 可以作为标识符的有“t3_”、“_t_3”、“_t3”、“_3t”四种,其中第1、2、4种可以由出栈序列得到,出入栈操作分别为IOIOIO、IOIIOO、IIIIOOO,因此选D。14.若栈采用顺序存储方式存储,现两栈共享空间 V [1⋯m],top [i] 代表第 i 个栈栈顶,栈 1 的底在 V [1],栈 2 的底在 V [m],则栈满的条件是( )。
A. |top [2] - top [1]| == 0
B. top [1] + 1 == top [2]
C. top [1] + top [2] == m
D. top [1] == top [2]14.【参考答案】 B
【解析】 栈1从V[1]往上增长,栈2从V[m]往下增长,则栈满时栈顶指针会在中间相遇,有些考生会误选D,对于D这种情况,若栈顶指针指向栈顶元素,则在top[1]==top[2]时,两个栈顶元素的位置重合了,若栈顶指针指向栈顶元素的后一个元素,则在top[1]==top[2]时,空了一个位置没有元素,因此D错误。15.对于单词 bookkeeper,按字母顺序进栈,则有多少种出栈顺序使其依然是原单词( )。
A. 8
B. 20
C. 12
D. 1615.【参考答案】 D
【解析】 对于bookkk的部分,oo可以按照IIOO也可以按照IOIO的形式得到,kk同理,共有2×2 = 4种方式可以得到,而eepe的部分,可以由IOIOIOIO、IIOOIOIO、IOIIIIOOO、IIOIIIOOO的形式得到,因此总共2×2×4 = 16种出栈序列仍然是bookkeeper。16.设栈的容量为 2,以 1,2,3,4,5 的顺序入栈(可随时出栈),出栈序列可能是( )。
A. 12345
B. 54321
C. 32145
D. 2154316.【参考答案】 A
【解析】 栈容量为2则不能在栈中存放2个以上的元素,A可由IOIOIOIOIO得到,栈中最多1个元素。B可由IIIIIIOOO000得到,栈中最多5个元素。C可由IIIIOOOIOIO得到,栈中最多三个元素。D可由IIOOIIIIOOO得到,栈中最多3个元素。17.若采用带头、尾指针的单向链表表示一个堆栈,那么栈顶指针 top 的设置方法为( )。
A. 将表头项设置为 top
B. 将链表尾设置为 top
C. 链表头、尾都适合作为 top
D. 链表头、尾都不适合作为 top17.【参考答案】 A
【解析】 由于对堆栈的入栈、出栈操作都是在top上进行的,如果将top设置在单链表的尾指针处,则每次访问top都需要从前往后遍历,会浪费大量时间,应放在头指针处比较合适。4.1.7 真题演练
18.【2010】若元素 a,b,c,d,e,f 依次进栈,允许进栈、退栈操作交替进行,但不允许连续三次进行退栈操作,则不可能得到的出栈序列是( )。
A. dcebfa
B. cbdaef
C. bcaefd
D. afedcb18.【参考答案】 D
【解析】 A可由IIIIOOOIOIOIO得到,B可由IIIIOOIOIOIO得到,C可由IIOIOOIIOIOO得到,都满足题意。而D可由IOIIIIIIOOO000得到,不符合题意。19.【2011】若元素 a,b,c,d,e 依次进入初始为空的栈中,若元素进栈后可停留、可出栈,直到所有元素都出栈,则在所有可能的出栈序列中,以元素 d 开头的序列个数是( )。
A. 3
B. 4
C. 5
D. 619.【参考答案】 B
【解析】 由于第一个出栈元素为d,则说明abc按顺序存在栈中,出栈顺序必为d_c_b_a_,e的顺序不定,可在任意一个“_”上,因此有4种。20.【2013】一个栈的入栈序列为 1,2,3,…,n,其出栈序列是 p₁,p₂,p₃,…,pₙ。若 p₂ = 3,则 p₃可能取值的个数是( )。
A. n - 3
B. n - 2
C. n - 1
D. 无法确定20.【参考答案】 C
【解析】 考虑3前面的元素1、2,可以通过IIOIOO得到出栈序列231或IOIIOO得到出栈序列132,考虑3后面的任意元素x,都可以在3出栈之后入栈到x后立刻出栈,如5可通过IOIIO(此时3出栈)IIO(入栈4、5,出栈5)得到,因此除了3本身以外,其他的值均可以取到,为n - 1个。21.【2018】若栈 S₁中保存整数,栈 S₂中保存运算符,函数 F () 依次执行下述各步操作:
①从 S₁中依次弹出两个操作数 a 和 b;②从 S₂中弹出一个运算符 op;
③执行相应操作 b op a;④将运算结果压入 S₁中。
假定 S₁中的操作数依次是 5,8,3,2(2 在栈顶),S₂中的运算符依次是 * - +(+ 在栈顶)。调用 3 次 F () 后,S₁栈顶保存的值是( )。
A. -15
B. 15
C. -20
D. 2021.【参考答案】 B
【解析】 按照题目给出步骤进行模拟,计算3 + 2 = 5,8 - 5 = 3,5×3 = 15。22.【2020】对空栈 S 进行 Push 和 Pop 操作,入栈序列 a,b,c,d,e,经过 Push,Push,Pop,Push,Pop,Push,Push,Pop 操作后,得到的出栈序列是( )。
A. b,a,c
B. b,a,e
C. b,c,a
D. b,c,e22.【参考答案】 D
【解析】 按照题目给出步骤模拟可得出栈序列为b,c,e。4.2 队列
4.2.1 队列的基本概念
队列(Queue)是一种遵循先进先出(FIFO,First - In - First - Out)原则的线性表,把进行插入的一端称为队尾,进行删除的一端称为队头 。如图4.9所示,元素在队尾入队,在队头出队。
这里举一个关于队列的例子:想象在食堂排队买饭,在队伍末端的人可以看成新插入的元素。那么排在最前面的人买完后“出队”,刚加入排队的人则是“入队”。
4.2.2队列的基本操作
除了进出方式与栈稍有不同,队列的其他操作与栈相似。
// 1. 初始化,构造一个空的队列 void initialize(Queue &Q); // 2. 插入元素,也称入队,在Q的队尾插入新的元素e bool enQueue(Queue &Q, ElemType e); // 3. 删除元素,也称出队,返回Q的队头元素 ElemType deQueue(Queue &Q); // 4. 获取队头元素,但不删除 ElemType getFront(const Queue &Q); // 5. 判空,判断Q是否为空队 bool queueEmpty(const Queue &Q);4.2.3队列的两种实现
队列同样能以顺序存储或链式存储的形式实现。由于队列的基本操作在队头和队尾进行,因此需要“队头指针”和“队尾指针”这两个指针。
1.顺序队列
采用顺序存储结构的队列称为顺序队列,它利用一组地址连续的存储单元存放整个队列的数据元素,并使用队头指针front与队尾指针rear定位队头和队尾。顺序队列的结构定义如下:
#define MAX_SIZE 100 typedef struct { ElemType data[MAX_SIZE]; int front, rear; // 队头指针和队尾指针 } SqQueue;rear有两种不同的定义方式:rear可以指向队尾元素,也可以指向队尾元素的下一个元素。
思考:对于顺序队列的判满操作,可以和顺序栈一样用rear == MAX_SIZE判断吗?
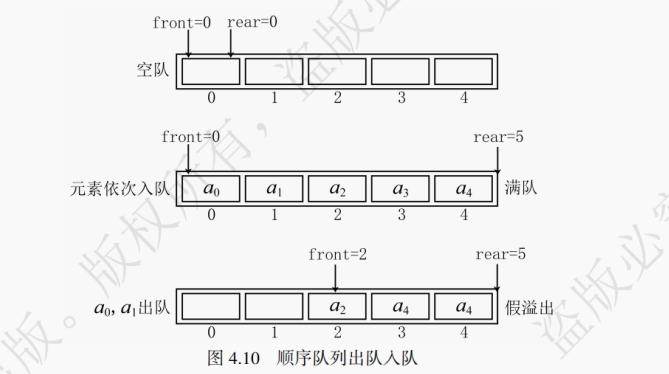
图4.10模拟了一组数据在顺序队列的入队与出队情况,在空队的情况下rear指向0(指向队尾的后一个元素)。当元素a₀,a₁出队列后依旧有rear == MAX_SIZE,此时并不是一个满队。然而此时即使队列中0、1位置可以存放新的数据元素,也无法再在队尾插入新的数据,这种情况被称为“假溢出”。
如图4.11所示,针对这种溢出现象,只需将空闲位置利用起来就可以解决。当出现假溢出时,如果还要再插入元素,则需将队尾指针移到空闲位置进行插入。在逻辑上让顺序队列“首尾相接”,得到一个环状的空间,这样就避免了假溢出的产生。
2.链式队列
队列可由队头指针和队尾指针代表整个链表,因此将队头指针和队尾指针放入一个结构体用来表示队列。此处给出链式队列的结构定义:
typedef struct QueueNode { // 链式队列的结点 ElemType data; struct QueueNode *next; } QueueNode; typedef struct { QueueNode *front, *rear; // 头尾指针 } LinkQueue;4.2.4循环队列的基本操作实现
循环队列是解决了假溢出问题的顺序队列,此处给出其各项基本操作的代码实现。
1.初始化队列
void initialize(SqQueue &Q) { Q.front = 0; Q.rear = 0; } SqQueue Q; initialize(Q);图4.12模拟了一组数据在循环队列的入队与出队情况,当rear指向MAX_SIZE后,再插入元素时,需将rear重新指向数组的起始位置,即下标为0的位置,这可以通过求余操作(MOD)实现。
在图 4.13 中,如果所有存储单元都存满了,则没有办法判断队空与队满(因为不论队空还是队满,front 和 rear 都指向了同一存储单元)。为此可以采取三种方法来解决这个问题:
(1) 空出一个单元来区分队空队满。当 rear == front 时为空队,当 (rear + 1) % MAX_SIZE == front 时为满队。
(2) 设置 size 数据成员,用于记录队列中元素的个数。当 size == 0 时为空队,当 size == MAX_SIZE 时为满队。
(3) 设置 flag 数据成员,开始时为空队,flag = 0。删除元素时将 flag 置 0,若删除元素后 front == rear 则为空队;添加元素时则将 flag 置 1,若添加元素后 front == rear 则为满队。
本书采用第一种方法来解决这个问题。
2.循环队列判空
bool queueEmpty(const SqQueue &Q) { return Q.front == Q.rear; }3.循环队列判满
bool queueFull(const SqQueue &Q) { // 取余是考虑rear指向MAX_SIZE的情况 return (Q.rear + 1) % MAX_SIZE == Q.front; }4.元素入队
bool enQueue(SqQueue &Q, ElemType e) { if (queueFull(Q)) return false; Q.data[Q.rear] = e; Q.rear = (Q.rear + 1) % MAX_SIZE; // 取余以达到循环的目的 return true; }5.元素出队
ElemType deQueue(SqQueue &Q) { if (queueEmpty(Q)) return ERROR; ElemType e = Q.data[Q.front]; Q.front = (Q.front + 1) % MAX_SIZE; return e; }4.2.5 链式队列的基本操作实现
如果采用没有头结点的链表作为链式队列,会导致插入与删除操作不统一,所以此处给出的是由有头结点的链表实现的链式队列,如图 4.14 所示。
1.初始化队列
void initialize(LinkQueue &Q) { Q.front = (QueueNode*)malloc(sizeof(QueueNode)); Q.front->next = NULL; Q.rear = Q.front; } LinkQueue Q; initialize(Q);2.链式队列判空
链式队列的判空与循环队列相同:
bool queueEmpty(LinkQueue Q) { return Q.front == Q.rear; }3.元素入队
bool enQueue(LinkQueue &Q, ElemType e) { QueueNode *q = (QueueNode*)malloc(sizeof(QueueNode)); if (q == NULL) // 分配空间失败 return false; q->data = e; q->next = NULL; // 插入队尾 Q.rear->next = q; Q.rear = q; // 队尾指针后移 return true; }4.元素出队
元素出队时需要注意的是:若队列中只有一个元素,那么出队之后需要将尾指针移至队头位置,否则会因为结点空间的释放导致尾指针指向未知的地址。
ElemType deQueue(LinkQueue &Q) { if (queueEmpty(Q)) return ERROR; QueueNode *p = Q.front->next; // 队头元素 ElemType e = p->data; Q.front->next = p->next; // 如果队列中只有一个元素,需要将队尾指针归位 if (Q.rear == p) Q.rear = Q.front; free(p); return e; }【例 4.4】栈和队列的主要区别在于( )
A. 它们的逻辑结构不一样
B. 它们的存储结构不一样
C. 所包含的元素不一样
D. 插入、删除操作的限定不一样
解析:选 D,对于 A,栈和队列的逻辑结构都是线性结构,故该选项不正确;对于 B,栈和队列都可以采用顺序存储或者链式存储,故该选项不正确;对于 C,栈和队列所含的元素可以是一样的,故该选项不正确;D 选项才是栈和队列的本质区别,栈和队列在插入、删除操作的限定不一样。4.2.6 双端队列
双端队列指的是在队列的两端都可以进行插入和删除操作的队列,这是一种对队列进行拓展而得到的数据结构。如图 4.15 所示,在双端队列上可以进一步限制插入和删除操作,得到插入受限的双端队列和删除受限的双端队列。
【例 4.5】若以 1、2、3、4 作为双端队列的输入序列,则既不能以插入受限的双端队列得到,也不能由删除受限的双端队列得到的出队序列是( )。
A. 1、2、3、4
B. 4、1、3、2
C. 4、2、3、1
D. 4、2、1、3
解析:设双端队列都是在其右端操作受限。对于 A,可以由插入受限的双端队列,输入 1、2、3、4,在右端输出 1、2、3、4 获得。对于 B,可以由插入受限的双端队列,输入 1、2、3、4,左出 4,右出 1,左出 3、2 得到。对于 D,可以由删除受限的双端队列,左入 1、2,右入 3,左入 4,出 4、2、1、3 获得。而 C 无法通过任何一种方法获得。同样在做这类题目的时候,画图进行模拟是最有效的方法。
提示:本节的重点在于理解队列的出入过程,包括队头指针和队尾指针的运动,以及循环队列的判满判空条件。4.2.7 习题精编
1.栈的特点是 (1),队列的特点是 (2),栈和队列都是 (3)。若进栈序列为 1234,则 (4) 不可能是一个出栈序列(不一定全部进栈后再出栈);若进队列的序列为 1234,则 (5) 是一个出队序列。
(1) A. 先进先出
B. 后进先出
C. 进优于出
D. 出优于进
(2) A. 先进先出
B. 后进先出
C. 进优于出
D. 出优于进
(3) A. 顺序存储的线性结构
B. 链式存储的线性结构
C. 限制存取点的线性结构
D. 限制存取点的非线性结构
(4) A. 4231
B. 1324
C. 3241
D. 3214
(5) A. 4231
B. 1234
C. 3241
D. 32141.【参考答案】B、A、C、A、B
【解析】这题是一道基础概念题,栈的特点是后进先出,队列的特点是先进先出,栈和队列都是限制存取点的线性结构。对于 1234 进栈,可由 IOIIOOIO 得 1324,IIIOOIOO 得 3241,IIIOOOIO 得 3214。2.若循环队列使用数组 A [m] 存放数据元素,已知头指针 front 指向队首元素,尾指针 rear 指向队尾元素后的空单元,则当前队列中的元素个数为( )。
A. (rear - front + m) % m
B. rear - front + 1
C. rear - front
D. rear - front - 12.【参考答案】A
【解析】假设 m 为 3,front 为 1,rear 为 0,则此时下标 1、2 的数组空间内有元素,即元素个数为 2。A 计算出为 2,其他选项计算出来均不正确。3.设栈 S 和队列 Q 的初始状态为空,元素 e1、e2、e3、e4、e5 和 e6 依次通过栈 S,一个元素出栈后即进队列 Q,若 6 个元素的出队序列是 e2、e4、e3、e6、e5、e1,则栈 S 的容量至少应该是( )。
A. 6
B. 4
C. 3
D. 23.【参考答案】C
【解析】出队序列对应着入队序列,也就对应着出栈序列,设 I 表示入栈,O 表示出栈,则操作顺序应该是 IIOIIOOIIIOOO,最大容量为 3。4.已知循环队列存储在 C 数组 A [m] 中,front 指向队头元素的前一个位置,rear 指向队尾元素,则当前队列中的元素个数为( )。
A. (rear - front + m) % m
B. (rear - front - m + 1) % m
C. (rear - front) % m
D. (rear - front - 1) % m4.【参考答案】A
【解析】本题的计算方法与第 2 题相同,只是 front 和 rear 都往后移动了一个位置。5.若用一个大小为 6 的数组来实现循环队列,且当前 rear 和 front 的值分别为 0 和 3,当从队列中删除一个元素,再加入两个元素后,rear 和 front 的值分别为( )。
A. 1、5
B. 2、4
C. 4、2
D. 5、15.【参考答案】B
【解析】删除一个元素则 front+1,插入两个元素则 rear+2,因此是 2 和 4。6.假设一个循环队列 Q 仅由队头指针 front,队尾指针 rear 和最大容量 m 组成,则判断该队列队满的条件是( )。
A. front == (rear + 1) % m
B. front == rear + 1
C. front == rear
D. rear == (front + 1) % m6.【参考答案】A
【解析】根据题中所给条件可以得到,该队列仅有队头指针队尾指针和最大容量,因此该队列只能通过牺牲一个数据元素位置来区分满或空,因此选 A。7.链队列由非循环单链表表示,队头是表尾,不设表尾指针,进队操作的时间复杂度是( )。
A. O (n²)
B. O (logn)
C. O (1)
D. O (n)7.【参考答案】C
【解析】非循环单链表不设表尾指针(队列头 front 是表尾),只设表头指针(指向队列的尾部),在队列中插入是在队尾插入,寻找队尾结点的时间复杂度是 O (1),因此插入复杂度也为 O (1)。8.循环队列与顺序队列的容量都为 MaxSize,其头指针为 front,尾指针为 rear,则空队列的条件分别为( )。
A. (rear + 1) % MaxSize == front
B. rear == front
C. (front + 1) % MaxSize == rear
D. rear == 08.【参考答案】B
【解析】循环队列与顺序队列的判空条件是相同的,当头尾指针重合时为空队列。9.设循环队列中数组的下标为 0 ~ N - 1,已知其队头指针 f(f 指向队首元素的前一个位置)和队中元素个数 n,则队尾指针 r(r 指向队尾元素的位置)为( )。
A. f - n
B. (f - n) % N
C. (f + n) % N
D. (f + n + 1) % N9.【参考答案】C
【解析】头指针加上元素个数就是尾指针位置,由于是循环队列,则还需取余。或采用特殊值法,假设 f = 3,n = 6,N = 7,则队列中 4、5、6、0、1、2 处有元素,此时 r 应该指向 2。10.最不适合用作链式队列的链表是( )。
A. 只带队首指针的非循环双链表
B. 只带队首指针的循环双链表
C. 只带队尾指针的循环双链表
D. 只带队尾指针的循环单链表10.【参考答案】A
【解析】队列需要经常对队首元素和队尾元素进行操作,因此需要链表可以在 O (1) 的时间复杂度访问到队首和队尾元素,A 只能访问到首或尾的其中一个(取决于队首在链表首还是链表尾),BCD 都可以在 O (1) 的时间复杂度内找到队首和队尾元素。11.已知循环队列存储在数组 A [m] 中,length 表示循环队列中的元素个数,rear 指向队尾元素,插入元素时执行 rear = (rear + 1) % m ,则 front 所在位置应该是( )。
A. rear - length
B. (rear - length + m) % m
C. (rear + m + 1 - length) % m
D. (rear + length - 1) % m11.【参考答案】C
【解析】由题给出条件可得队首在 rear - (length - 1) 的位置(因为 rear 占一个位置),由于减法可能结果为负数,考虑到循环特性,需要加上 m 再对 m 取模。或特殊值法:取 m = 3,length = 2,rear = 0,则此时 front 在 2 的位置,带入计算,C 满足条件。12.在链队列中,队首指针为 front,队尾指针为 rear,将 x 所指向的结点入队,其操作为( )。
A. front = x; front = front->next;
B. x->next = front->next; front = x;
C. rear->next = x; rear = x;
D. rear->next = x; x->next = null; rear = x;12.【参考答案】D
【解析】进队操作在队尾进行,则 D 有 (1) 接到队尾:rear->next = x;(2) 队尾指向空:x->next = NULL;(3) 转移队尾指针:rear = x;三步操作。13.(多选)已知输入序列为 abcd,经过输出受限的双向队列后能得到的输出序列有( )。
A. dacb
B. cabd
C. dbca
D. bdac13.【参考答案】B,D
【解析】设队列右端仅能输入,左端既能输入又能输出。对于 B,可由 a 左入,b 右入,c 左入,d 右入,之后依次出队获得。设队列左端仅能输入,右端既能输入又能输出。对于 D,可由 a 右入,b 右入,b 右出,c 左入,d 右入,然后依次右出 dac 即得结果。14.设输入元素序列为 1,2,3,4,5,利用两个队列,下面哪种排列不可能得到?( )。
A. 1,2,3,4,5
B. 5,2,3,4,1
C. 1,3,2,4,5
D. 4,1,5,2,314.【参考答案】B
【解析】由于队列有先进先出的特性,两个辅助队列,最多有两条升序排列,B 选项 5、2、3、4、1 共三个升序排列,故 B 选项错误。4.2.8 真题演练
15.【2009】设栈 S 和队列 Q 的初始状态均为空,元素 a、b、c、d、e、f、g 依次进栈 S。若每个元素出栈后立即进入队列 Q,且 7 个元素出队的顺序是 b、d、c、f、e、a、g,则栈 S 的容量至少是( )。
A. 1
B. 2
C. 3
D. 415.【参考答案】C
【解析】队列先进先出,则出队顺序对应了出栈顺序。按照如下顺序:a、b 入栈,b 出栈,c、d 入栈,d、c 出栈,e、f 入栈,f、e、a 出栈,g 入栈,g 出栈。因此栈的容量最少为 3。16.【2010】某队列允许在其两端进行入队操作,但仅允许在一端进行出队操作。若元素 a、b、c、d、e 依次入此队列后再进行出队操作,则不可能得到的出队序列是( )。
A. bacde
B. dbace
C. dbcae
D. ecbad16.【参考答案】C
【解析】A 可由左入、左入、右入、右入、右入得到。B 可由左入、左入、右入、左入、右入得到。D 可由左入、左入、左入、右入、左入得到。C 左入、右入,此时 d 未出,只能继续进队,故 C 错误。17.【2011】已知循环队列存储在一维数组 A [0, …, n - 1] 中,且队列非空时 front 和 rear 分别指向队头元素和队尾元素。若初始时队列是空,且要求第 1 个进入队列的元素存储在 A [0] 处,则初始时 front 和 rear 的值分别是( )。
A. 0,0
B. 0,n - 1
C. n - 1,0
D. n - 1,n - 117.【参考答案】B
【解析】因为 rear 指针指向的是队尾元素,所以新元素的入队过程是:rear 先加 1 以指向新的空位置,然后新元素加入队列的 rear 处。所以只有当 rear 指针初始化成 n - 1,在添加第一个元素的过程中,先 n - 1 加 1 变成 0(因为队列是循环队列的原因),然后在 rear = 0 处加入第一个元素,如此就可以满足题意了。18.【2014】循环队列放在一维数组 A [0, …, M - 1] 中,end1 指向队头元素,end2 指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳 M - 1 个元素。初始时为空。下列判断队空和队满的条件中,正确的是( )。
A. 队空:end1 == end2; 队满:end1 == (end2 + 1) mod M;
B. 队空:end1 == end2; 队满:end2 == (end1 + 1) mod (M - 1);
C. 队空:end2 == (end1 + 1) mod M; 队满:end1 == (end2 + 1) mod M;
D. 队空:end1 == (end2 + 1) mod M; 队满:end2 == (end1 + 1) mod (M - 1);18.【参考答案】A
【解析】end1 指向队头元素,end2 指向队尾元素的后一个元素,队空时队头与队尾指针重合,队满时容纳 M - 1 个元素,即空出一个元素用来判断队满,可得当 end1 == end2 + 1 时为队满,又因为该队列为循环队列,则需要对 m 进行取余操作。可以画一个只有两个存储单元的循环队列,进行模拟操作即可。19.【2018】现有队列 Q 与栈 S,初始时 Q 中的元素依次是 1、2、3、4、5、6(1 在队头),S 为空。若仅允许下列三种操作:① 出队并输出出队元素;② 出队并将出队元素入栈;③ 出栈并输出出栈元素,则不能得到的输出序列是( )。
A. 1、2、5、6、4、3
B. 2、3、4、5、6、1
C. 3、4、5、6、1、2
D. 6、5、4、3、2、119.【参考答案】C
【解析】A 的操作过程为:1 (出队) 1 (出队) 2 (入栈) 2 (入栈) 1 (出队) 1 (出队) 3 (出栈) 3 (出栈)。B 的操作过程为:2 (入栈) 1 (出队) 1 (出队) 1 (出队) 1 (出队) 1 (出队) 1 (出队) 3 (出栈)。D 的操作过程为:2 (入栈) 2 (入栈) 2 (入栈) 2 (入栈) 1 (出队) 3 (出栈) 3 (出栈) 3 (出栈) 3 (出栈) 3 (出栈)。对于选项 C,输出元素 3,只能先将元素 1、2 入栈,按照 1、2 的顺序入栈,则出栈的顺序为 2、1,因此不会出现 C 选项中 1、2 的输出序列。20.【2021】已知初始为空的队列 Q 的一端仅能进行入队操作,另外一端既能进行入队操作又能进行出队操作,若 Q 的入队序列是 1、2、3、4、5 则不能得到的出队序列是( )。
A. 5、4、3、1、2
B. 5、3、1、2、4
C. 4、2、1、3、5
D. 4、1、3、2、520.【参考答案】D
【解析】假设队列右端仅能入队,则题中所给 ABCD 选项就是数据在队列中的排列,因为出队必须从左端进行。A 可由右入 1、2,左入 3、4、5 得到。B 可由右入 1、2,左入 3,右入 4,左入 5 得到。C 可由左入 1、2,右入 3,左入 4,右入 5 得到。而 D 中 1 和 2 中隔了一个 3,无法得到。21.【2019】请设计一个队列,要求满足:① 初始时队列为空;② 入队时,允许增加队列占用空间;③ 出队后,出队元素所占用的空间可重复使用,即整个队列所占用的空间只增不减;④ 入队操作和出队操作的时间复杂度始终保持为 O (1)。请回答下列问题:
(1) 该队列应该选择链式存储结构,还是顺序存储结构;
(2) 画出队列的初始状态,并给出判断队空和队满的条件;
(3) 画出第一个元素入队后的队列状态;
(4) 给出入队操作和出队操作的基本过程。21.(1)采用链式存储结构(单循环链表)。
(2)队列初始状态如图 4.16 所示。以 front 为队头,rear 为队尾,队空的条件为 front == rear,队满的条件为 front == rear->next。
(3)插入第一个元素后的状态如图 4.17 所示。
(4)入队和出队操作的伪代码描述如下:
① 入队操作的过程描述如下:
判断队列的状态。如果队列满(front == rear->next),队列中已经没有空结点,需要新建一个结点,把结点插入到队尾 rear 后面。用 e 表示入队元素,令:rear -> data = e; rear = rear -> next。
② 出队操作的过程描述如下:
判断队列的状态。若队列为空(front == rear),队列中没有可以出队的元素,出队失败,返回空值。若队列非空,则用 e 表示出队元素,令 e = front -> data; front = front -> next。最后返回 e。4.3 栈与队列的应用
1.(多选) 栈可以应用在( )。
A. 递归、表达式求解
B. 表达式转化、缓冲区
C. 迷宫求解、括号匹配
D. 进制转换
1.【参考答案】A、C、D
【解析】递归,表达式求解,表达式转化,括号匹配都是栈的典型应用,缓冲区是队列的典型应用。在迷宫求解时,可以将走过的路径依次压栈,当遇到死路时,依次出栈则可以原路返回。在进制转换时,可以将每次短除法的余数依次压栈,最终依次弹出,这样就完成了进制转换。4.3.1 栈在括号匹配中的应用
括号匹配的规则是:每个右括号都与其前面最近的、且尚未配对的同类型左括号相匹配。利用栈将当前尚未配对的左括号存入栈中,栈顶处即是最新未配对的左括号,匹配时则弹出栈顶元素。即括号序列和出入栈序列具有形式一致性,左括号和右括号和 push/pop 是对应关系。应用栈进行括号匹配的算法描述如下:
(1)从左到右扫描括号序列,若遇到左括号则入栈。
(2)遇到右括号和栈顶元素比较:①若当前扫描元素(右括号)与栈顶元素(左括号)是相同类型的括号,则说明其中一对括号匹配成功,弹出栈顶元素,继续扫描括号序列;②若当前扫描元素(右括号)与栈顶元素(左括号)是不同类型括号,则说明括号匹配失败。
(3)括号序列扫描完成后,若栈不为空,说明还有未匹配的左半括号,则匹配失败;若栈为空,则括号匹配成功。
提示:应用栈进行括号匹配过程中,将当前尚未配对的左括号存入栈中,栈顶处即是最新未配对的左括号,匹配时则弹出栈顶元素。匹配成功时,每一个入栈操作对应遇到一个左括号,每一个出栈操作对应遇到一个右括号,左括号、右括号和入栈(push)、出栈(pop)操作一一对应。
如图4.18所示,以括号序列 “[()()]” 为例,括号匹配的过程如下:
(1)初始为空栈,扫描①、②,遇到左括号依次入栈。
(2)遇到右括号③,与栈顶元素比较,若匹配成功,则出栈一个元素。扫描④、⑤,遇到左括号,入栈。
(3)扫描⑥、⑦,遇到右括号,与栈顶元素比较,匹配成功,依次出栈。
(4)扫描⑧,遇到右括号,与栈顶元素不匹配,匹配失败。
4.3.2 栈在表达式求值中的应用
1.基本概念
表达式求值在 408 考试中常考,选择题和大题中都考过,考生有必要透彻的理解掌握。
中缀表达式指运算符位于两个操作数中间的表达式,是最为常用的算术表示方式。我们从小学习的其实就是中缀表达式。
中缀表达式的运算规则是:按照从左到右的次序,先计算乘除、后计算加减,遇到括号,先计算括号内的部分。在计算中缀表达式时,不仅要考虑运算符的优先级,还要考虑括号。虽然它符合人类的思维习惯,但却不容易被计算机解析。
后缀表达式(又称为逆波兰表达式)指运算符在操作数后面的表达式。后缀表达式只有运算符和操作数,没有括号,在计算时,按照从左到右的次序处理,无需考虑运算符优先级。后缀表达式容易被计算机解析处理。2.中缀表达式转为后缀表达式
中缀表达式转为后缀表达式时,要借助一个栈来实现。从左往右扫描中缀表达式 exp,用 ch 表示 exp 的当前元素,用 sk 表示转换过程中用到的栈(暂存 exp 中的运算符),用 res 表示 exp 对应的后缀表达式(res 是结果队列,先进先出)。中缀表达式 exp 转为对应的后缀表达式 res 的计算过程如下:
注意:在所有的运算符中,“(” 运算优先级是最低的。
(1)若 ch 是数字,则将 ch 放入 res 中。
(2)若 ch 是运算符:
1.若 ch 运算优先级小于或等于 sk 的栈顶元素,则不断将 sk 出栈,并将 sk 中出栈的元素放入 res 中,直到 ch 运算优先级大于 sk 的栈顶元素或栈空为止。最后将 ch 放入栈 sk 中。例如:若 ch 是 “+”、栈顶元素是 “-”,或 ch 是 “+”、栈顶元素是 “*”,则将 sk 出栈。
2.若 ch 运算优先级大于 sk 的栈顶元素,则将 ch 放入栈 sk 中。例如:若 ch 是 “*” 或 “/”,栈顶元素是 “+” 或 “-”,则将 ch 放入栈 sk 中。
3.若 ch 是 “(”,则将 ch 放入栈 sk 中。
4.若 ch 是 “)”,则不断将 sk 出栈,并将 sk 中出栈的元素放入 res 中,直到遇到 “(” 为止。最后将 “(” 出栈,但不放入 res 中。这一步保证了 res 中没有括号。
(3)若 exp 扫描完毕,则将栈 sk 中的元素全部出栈,并放入 res 中。
根据上面的介绍,将中缀表达式转为对应的后缀表达式的示例,如表4.1所示:
以中缀表达式 exp = 8 - (1 + 2) * 2 + 10 / 2 为例,将其转为对应的后缀表达式的手工计算方法:
(1)拆分法:
运算单元由 “操作数 a、运算符 op、操作数 b” 组成。这里操作数 a、操作数 b 也可以分别是表达式的值,也可以看作一个大的运算单元。一个大的运算单元由若干个小的运算单元组成。从最内层(不能再分解)的运算单元开始,将运算符移到操作数后面。操作步骤如下:(a)将 exp 分解成:操作数 a = 8 - (1 + 2) * 2,运算符 op = “+”,操作数 b = 10 / 2。
(b)将操作数 a 再分解成:操作数 a1 = 8,运算符 op = “-”,操作数 b1 = (1 + 2) * 2。
(c)将操作数 b1 再分解成:操作数 b11 = (1 + 2),运算符 op = “*”,操作数 b22 = 2。
(d)对于每一个运算单元,将运算符移到操作数后面:运算单元 b11 调整为:1 2 +,运算单元 b1 调整为:1 2 + 2 *,运算单元 a 调整为:8 1 2 + 2 * -,运算单元 b 调整为:10 2 /。
(e)将调整后的结果合并,可得对应的后缀表达式为:8 1 2 + 2 * - 10 2 / + 。
(2)括号法:
(a)从左到右,按照中缀表达式的计算顺序对所有的运算单元加括号。例如:上述中缀表达式总共有:m1 = (1 + 2)、m2 = (1 + 2) * 2、m3 = 8 - (1 + 2) * 2、m4 = 10 / 2、m5 = 8 - (1 + 2) * 2 + 10 / 2 这 5 个运算单元。
对 m1、m2、m3、m4、m5 加括号,可得:m11 = ((1 + 2))、m22 = (((1 + 2) * 2))、m33 = (8 - ((1 + 2) * 2))、m44 = (10 / 2)、m55 = (8 - ((1 + 2) * 2) + (10 / 2))。
将 m11、m22、m33、m44 代入 m55,可得:m = ((8 - (((1 + 2) * 2))) + ((10 / 2)));(b)把所有的运算符移动到对应的右括号后面。得到:((8 ((((1 + 2)) * 2)) - )((10 2) / ) + ;
(c)去掉所有括号,即可得到对应的后缀表达式,即:8 1 2 + 2 * - 10 2 / + 。
3.后缀表达式的求值
后缀表达式的运算过程如下:从左往右扫描表达式,若遇到操作数则入栈,若遇到运算符则连续出栈两个元素,和运算符进行运算(先出栈的元素放在运算符的右边,后出栈的元素放运算符左边,即:次栈顶 运算符 栈顶),并将运算结果存入栈中,最后出栈元素值即为表达式的值。
这里以一个实例,演示后缀表达式的求值过程。后缀表达式为:8 1 2 + 2 * - 10 2 / + ,计算步骤如下:
(1)首先初始化一个空栈,依次从左到右扫描表达式。
(2)扫描到操作数 8、1、2,依次入栈。
(3)扫描到运算符加号 (+),则连续出栈两次,得到 2、1,与运算符 (+) 进行运算 (1 + 2 = 3),将运算结果 3 入栈。
(4)扫描到操作数 2 入栈,扫描到运算符乘号 (),则连续出栈两次,得到 2、3,与运算符 () 进行运算 (3 * 2 = 6),将运算结果 6 入栈。
(5)扫描到运算符减号 (-),则连续出栈两次,得到 6、8,与运算符 (-) 进行运算 (8 - 6 = 2),将运算结果 2 入栈。
(6)扫描到操作数 10、2,依次入栈。
(7)扫描到运算符除号 (/),则连续出栈两次,得到 2、10,与运算符 (/) 进行运算 (10 / 2 = 5),将运算结果 5 入栈。
(8)扫描到运算符加号 (+),出栈 5、2,与运算符 (+) 进行运算 (2 + 5 = 7),将运算结果 7 入栈。
(9)遍历结束,出栈 7 即为运算结果。
上述计算过程,考生可以结合图4.19理解。
4.前缀表达式
前缀表达式(又称为波兰表达式)指运算符在操作数前面的表达式。前缀表达式也没有括号,计算时无需考虑运算符优先级。
实际上前缀 / 后缀的运算符和 push/pop 也是一一对应的关系。前缀表达式要从右往左扫描表达式,其他的计算步骤都是一样的。
前缀表达式计算过程如下:从右往左扫描前缀表达式,若遇到操作数则入栈,若遇到运算符则连续出栈两个元素,和运算符进行运算(先出栈的元素放在运算符的左边,后出栈的元素放运算符右边,即:栈顶运算次栈顶),并将运算结果存入栈中,最后出栈元素值即为表达式的值。中缀表达式转化成对应的后缀表达式时,介绍了 2 种手工转换方法(拆分法和括号法),这 2 种方法也可用于将中缀表达式转换为对应的前缀表达式。区别在于:中缀转化为前缀表达式时,使用拆分法时,要将运算符移到操作数前面;使用括号法时,要将运算符移动到对应的括号前面。其他的计算步骤都是一样的。
以中缀表达式:8−(1+2)∗2+10/2为例,使用括号法将中缀表达式转换为对应前缀表达式的过程如下:
(1)从左到右,对所有的运算单元加括号,式子变成:((8−(((1+2))∗2))+((10/2)));
(2)把所有的运算符号移动到对应的括号前面,得到:+(−(8(∗(+(12))2))/(102));
(3)去掉所有括号,即可得到对应的前缀表达式,即:+−8∗+122/102 。
将中缀表达式转化为后缀表达式或前缀表达式时,要去掉括号,但操作数之间的的相对顺序保持不变。考生可以根据这点初步验证转换后的结果。
5. 栈在递归中的应用
在编程基础一章已讲解递归函数的执行过程,递归函数只有在最终达到返回条件时才会进行返回,而每次进行递归调用的函数都需要等待深一层的函数执行完毕后才能继续执行。也就是说,在进行递归函数调用时,每一层的函数都未返回,直到递归进行到最后一层时才会返回,并继续执行上一层的函数。可以用栈来实现这些功能,每进行深一层的递归调用,便将当前层入栈,直到最后一层返回,按与压栈相反的顺序将函数一层层从栈中弹出,直到回到最初开始运行的函数为止,最终得到递归函数的返回值。
可以利用显式的栈来模拟递归过程,从而将递归程序转化为迭代程序。
4.3.3 习题精编
1.(多选) 栈可以应用在( )。
A. 递归、表达式求解
B. 表达式转化、缓冲区
C. 迷宫求解、括号匹配
D. 进制转换
1.【参考答案】A、C、D
【解析】递归,表达式求解,表达式转化,括号匹配都是栈的典型应用,缓冲区是队列的典型应用。在迷宫求解时,可以将走过的路径依次压栈,当遇到死路时,依次出栈则可以原路返回。在进制转换时,可以将每次短除法的余数依次压栈,最终依次弹出,这样就完成了进制转换。2.(多选) 队列可以运用在( )。
A. 缓冲区
B. 迷宫求解
C. 递归
D. 消息队列
2.【参考答案】A、B、D
【解析】缓冲区和消息队列是队列的经典应用。迷宫问题除了可以用栈来求解,也可使用队列求解。3.下列说法中,正确的是( )。
A. 消除递归必须用栈
B. 函数调用通常会使用队列
C. 队列和栈都允许在两端进行操作
D. 表达式求值可以不借助栈
3.【参考答案】D
【解析】消除递归有很多办法,迭代也可以用来消除递归,只需要简单的循环就可以完成。函数调用通常会使用栈,将函数地址压栈,退出被调用函数时从栈中弹出地址并返回。栈只允许在一端进行操作。表达式求值有很多办法,使用栈只是其中的一种。4.通常情况下,一个问题的递归算法相比于非递归算法而言( )。
A. 效率更高
B. 效率更低
C. 两者相同
D. 无法比较
4.【参考答案】B
【解析】递归算法在实际执行过程中包含很多的重复计算,因此效率会低一些。5.中缀表达式(A+B)∗(C−D)/(E−F∗G)的后缀表达式是( )。
A. A+B∗C−D/E−F∗G
B. AB+CD−∗EF∗G−/
C. AB+C∗D−E−F/G∗
D. ABCDEFG+∗−/−∗
5.【参考答案】B
【解析】这类题目可以从选项出发,通过模拟计算后缀表达式的结果与中缀表达式比较得出答案,也可以通过本节中所说的办法将中缀表达式转化成后缀表达式获得。A 不符合后缀表达式的形式,D 先计算 F + G,显然不对。对于 C,若进行计算,弹出 AB + 执行 A + B 压栈,弹出 C*,相当于执行 (A + B)C,错误。对于 B,弹出 AB + 执行 (A + B),压入 (A + B),弹出 (A + B),C,D,-,执行 (C - D),压入 (C - D),(A + B),再弹出至,执行 (A + B)*(C - D),后面也都符合表达式。6.利用栈求表达式的值时,设立操作符栈 SK,若栈 SK 只有两个存储单元,在下列表达式中,不发生上溢的是( )。
A. A−B∗(C−D)
B. (A−B)∗C−D
C. (A−B∗C)−D
D. (A−B)∗(C−D)
6.【参考答案】B
【解析】①对于 A,操作符‘ - ’入栈后,下一个操作符‘’的优先级高于操作符‘ - ’,则操作符‘’入栈,遇到操作符‘(’时需要入栈,则栈溢出。②对于 C,操作符‘(’和操作符‘ - ’依次入栈,下一个操作符‘’的优先级高于‘ - ’,操作符‘’需要入栈,则栈溢出。③对于 D,操作符‘(’和操作符‘ - ’依次入栈,遇到操作符‘)’全部弹出变为空栈,而后操作符‘’(- ‘依次入栈,栈溢出。④对于 B,操作符‘(’和‘ - ’依次入栈,遇到操作符‘)’全部弹出变空栈,而后操作符‘’和‘ - ’依次入栈,遍历完毕依次退栈,输出序列为AB−C∗D−。7.C 语言函数 calc 的定义如下,a,b 均为正整数,则 calc (a,b) 的运行结果是( )。
int calc(int x, int y) { if (y == 1) return x; else return calc(x, y - 1) + x; }A. a∗(b−1)
B. a∗b
C. a+b
D. a+a
7.【参考答案】B
【解析】calc (a,b) 在 b 不等于 1 的时候等价于 calc (a,b - 1) + a,递归执行到第二个操作数为 1,则相当于执行了 b - 1 次 calc,递归返回再加上最后一次返回的 a,则相当于计算了 ab。设 a = 2,b = 2,第一次执行 calc (3,2)=calc (3,1)+3,calc (3,1)=3,则 calc (3,2)=32=6。8.设递归函数如下,问 func (func (5)) 在执行过程中,第 4 个开始被执行的 func 是( )。
int func(int x) { if (x <= 3) return 2; else return func(x - 2) + func(x - 4); }A. func(2)
B. func(3)
C. func(4)
D. func(5)
8.【参考答案】C
【解析】首先执行 func (5) = func (3)+func (1) = 4,共三次,再执行 func (func (5)) = func (4) = func (2)+func (0)=4,因此第四个被执行的 func 是 func (4)。9.用栈来检查算术表达式中的括号是否匹配的方法是:初始栈为空,从左到右扫描表达式,遇到 “(” 就将其入栈,遇到 “)” 就执行出栈操作。检查算术表达式 “((a + b (a + b) - c) a)/b” 时,由于( ),该表达式中的括号不匹配。
A. 栈为空却要进行出栈操作
B. 栈已满却要进行入栈操作
C. 表达式处理已结束,栈中仍留有字符 “(”
D. 表达式处理已结束,栈中仍留有字符 “)”
9.【参考答案】C
【解析】利用栈来检查算术表达式中的括号是否匹配,当遇到 “(” 时将其入栈,当遇到 “)” 时需要将此时的栈顶 “(” 出栈,所以每个 “)” 可以匹配一个 “(”,题中表达式有 3 个 “(”,2 个 “)”,所以会剩余一个 “(”,答案选 C。4.3.4 真题演练
10.【2009】为解决计算机主机与打印机之间速度不匹配问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是( )。
A. 栈
B. 队列
C. 树
D. 图
10.【参考答案】B
【解析】缓冲区打印需要先进先出,显然是队列。11.【2012】已知操作符包括 +、-、*、/、(、)。将中缀表达式a+b−a∗(c+d)/e−f)+g转换为等价的后缀表达式ab+acd+e/f−∗−g+时,用栈来存放暂时还不能确定运算次序的操作符,若栈初始时为空,则转换过程中同时保存在栈中的操作符的最大个数是( )。
A. 5
B. 7
C. 8
D. 11
11.【参考答案】A
【解析】a 输出,+ 入栈,b 输出,遇到 + 时,+ 出栈 - 入栈(同优先级),a 输出,* 入栈(乘除的优先级高于加减),两个左括号入栈,c 输出,+ 入栈,d 输出,此时栈中为 - *(+(,遇到右括号出栈到左括号,/ 入栈,e 输出,遇到 / 时,/ 出栈 - 入栈(乘除的优先级高于加减),遇到右括号出栈到左括号,遇到 + 时,* 出栈 - 出栈 + 入栈,g 输出,遍历结束依次退栈,因此栈中最多 5 个操作符。具体转换过程如下表,可以看出栈中的操作符的最大个数是 5,选 A。

12.【2014】假设栈初始为空,将中缀表达式a/b+(c∗d−e∗f)/g转换为等价的后缀表达式的过程中,当扫描到 f 时,栈中的元素依次是( )。
A. +(∗−
B. +(−∗
C. /+(∗−∗
D. /+−∗
12.【参考答案】B
【解析】按照书中给出的步骤模拟即可得出。
13.【2015】已知程序如下,程序运行时使用栈来保存调用过程的信息,自栈底到栈顶保存的信息依次对应的是( )。
int S(int n) { return (n <= 0)? 0 : S(n - 1) + n; } int main() { cout << S(1); }A. main()→S(1)→S(0)
B. S(0)→S(1)→main()
C. main()→S(0)→S(1)
D. S(1)→S(0)→main()
13.【参考答案】A
【解析】函数调用栈返回与调用顺序相反。最先执行 main () 函数,main () 函数里调用了 S (1),S (1) 里面又递归调用了 S (0),即 main ()、S (1)、S (0) 依次进栈,因此选 A。14.【2016】设有如下图所示的火车车轨,入口到出口之间有 n 条轨道,列车的行进方向均为从左至右,列车可驶入任意一条轨道。现有编号为 1 - 9 的 9 列列车,驶入的次序依次是 8、4、2、5、3、9、1、6、7。若期望驶出的次序依次为 1 - 9,则 n 至少是( )。
A. 2
B. 3
C. 4
D. 5
14.【参考答案】C
【解析】入队顺序为 8、4、2、5、3、9、1、6、7,出队顺序为 1 - 9。显然在同一条队列中先入队的元素必须小于后入队的元素,若 8、4 入同一条队列,则 8 必然在 4 的前面出队。这样 8 入队 a,4 只能入队 b,2 只能入队 c。为了保证同一队列内元素大小顺序,5 可以入队 b,3 入队列 c,9 入队 a,1 入队列 d,6、7 依次入队 b 即可。15.【2017】下列关于栈的叙述中,错误的是( )。
I. 采用非递归方式重写递归程序时必须使用栈
II. 函数调用时,系统要用栈保存必要的信息
III. 只要确定了入栈顺序,即可确定出栈次序
IV. 栈是一种受限的线性表,允许在其两端进行操作
A. 仅 I
B. 仅 I、II、III
C. 仅 I、III、IV
D. 仅 II、III、IV
15.【参考答案】C
【解析】迭代实现斐波那契数列只需一个循环不需要栈,故 Ⅰ 错误。入栈顺序为 1、2,若 push、push、pop、pop 出栈次序为 2、1,若执行 push、pop、push、pop 出栈顺序为 1、2,故 Ⅲ 错误。栈只允许在一边操作,故 Ⅳ 错误。4.4 数组与矩阵压缩存储
4.4.1 数组的基本概念
数组是 n 个相同类型数据元素构成的有限序列。数组中的元素被存储在一段连续的内存空间中。矩阵在计算机中就表示为一个 m 维数组。
1.一维数组
如图 4.21 所示,一维数组中每个存储单元的地址可以用以下公式计算得到:
Addr(ai)=Addr(a0)+i×L
其中,L 是每个存储单元的长度。
2.多维数组
对于多维数组,也有相似的结论。以二维数组为例,二维数组指的就是存储的数据类型都是一维数组的一维数组。每一个外层一维数组的数据单元里存储的都是相同尺寸的一维数组,如图 4.22 所示。
推广到 n 维数组,指的就是存储 n - 1 维数组的一维数组。
如图 4.23 所示,二维数组在存储时可以按照行优先或列优先的方式存储,对于数组 a [m][n],
若按照行优先,可得存储单元地址计算公式为:
Addr(aij)=Addr(a00)+[i×n+j]×L
若按照列优先,可得存储单元地址计算公式为:
Addr(aij)=Addr(a00)+[j×m+i]×L
4.4.2 特殊矩阵的压缩存储
特殊矩阵指值相同的元素或者零元素在矩阵中的分布有一定规律的矩阵。压缩存储是指对于多个值相同的元素只分配一个存储空间。
特殊矩阵主要有以下四种形式:(1) 对称矩阵;(2) 上 / 下三角矩阵;(3) 稀疏矩阵;(4) 三对角矩阵。除了稀疏矩阵,其他三种矩阵都是方阵(行数和列数相等的矩阵),本节将以矩阵Ann来代表 n 阶方阵。1.对称矩阵
对称矩阵是指以主对角线为对称轴,各个对称位置的元素相等的矩阵,即aij=aji。一个 n 阶对称矩阵Ann(1≤i,j≤n) 如下所示:
根据图4.24所示,根据对称矩阵aij=aji的性质,只存储对角线一侧的数据。若将该矩阵的下三角部分,按照行优先的形式存储到数组B[n(n+1)/2]中,数组 B 实际上就包含了Ann矩阵中的所有信息,这样就达到了压缩矩阵的目的。
设对称矩阵Ann中的元素aij,存储在B[k]中。第一行有 1 个元素,第二行有 2 个元素,一直到第 i 行的开头,总共存了[1+(i−1)]×(i−1)/2个元素。因此在下三角矩阵Ann中,第 i 行的第 j 个元素aij,在数组 B 中的下标 k,可由以下的公式求得 (注意数组下标从 0 开始):
其中矩阵的上半部分只需要由对称矩阵的性质:aij=aji,即可求得。2.上 / 下三角矩阵
主对角线以下 / 上都是常数 c 的方阵称为上 / 下三角矩阵。例如:Ann(1≤i,j≤n)是一个上三角矩阵,Ann′是一个下三角矩阵。
针对上 / 下三角矩阵的特点,只存储矩阵主对角线以上 / 以下区域中的元素,并用一个数组元素来存储半个矩阵的常数数据,即可达到节省存储空间(压缩存储)的目的。
上 / 下三角矩阵的存储和对称矩阵的存储基本相同,唯一不同的一点就是:要在数组的末尾加入常数 c。上 / 下三角矩阵中的元素aij存储在数组B[k]中,下标 k 的计算公式如下:下三角矩阵:
上三角矩阵:
3.稀疏矩阵
在矩阵中,若数值为 0 的元素数目远多于非 0 元素的数目,并且元素分布没有规律时,则称该矩阵为稀疏矩阵。例如,如下所示的矩阵A44是一个稀疏矩阵。
稀疏矩阵中每一个非零元素由一个三元组(aij,i,j)唯一确定(1≤i,j≤n),稀疏矩阵中所有非零元素构成一个三元组线性表。三元组(aij,i,j)中aij指非零元素的值、i 和 j 指元素aij在矩阵中的位置,例如:对于上述稀疏矩阵A44,对应的三元组为:
(2,1,1):数据元素为 2,在矩阵中的位置为 (1,1);
(3,4,1):数据元素为 3,在矩阵中的位置为 (4,1);
(4,4,4):数据元素为 4,在矩阵中的位置为 (4,4)。
稀疏矩阵A44对应的三元组线性表为:((2,1,1),(3,4,1),(4,4,4))。
但是要注意,采用这种方法存储稀疏矩阵会导致矩阵失去随机存取的特性。在本书第 6.2.3 小节中介绍的十字链表也可以用于稀疏矩阵的存储。同时在存储稀疏矩阵时,使用三元组表示非零元素是一种常见的方法。然而,仅凭三元组本身是无法完全还原原始的稀疏矩阵的,因为我们无法从中得知矩阵的行数和列数。因此,在存储稀疏矩阵时,除了使用三元组来表示非零元素外,还需要额外保存矩阵的行数和列数。这样,在还原矩阵时,我们可以根据保存的行数和列数信息创建一个具有正确维度的零矩阵,并将三元组中的非零元素按照其对应的行列索引填入正确的位置。2.三对角矩阵
在三对角矩阵中,所有的非零元素都集中在以主对角线为中心的三条对角线的区域,而其他区域的元素都为某个常数 c (如 0)。三对角矩阵又称带状矩阵,其结构如下所示:
同样,三对角矩阵也可以按照行优先的存储方法,将其存放在一维数组 B 中。除了第一行和最后一行中有两个元素需要存储,其余各行都有 3 个元素。如图4.25所示。
观察上图可得,每行的元素aij实际上是第i(i≠1)行的第j+2−i个非零元素,到第i行(i=1)的开头,B 中已经存储了2+3×(i−2)个元素。aij在数组 B 中的下标 k 的计算公式为:
提示:下标的计算公式,考试一般考选择题,考生学会推导并准确记忆公式可加快解题速度。对于选择题,考生也可以通过特殊值法、排除法确定正确选项。4.4.3 习题精编
1.用足够容量的一维数组 B 对 n×n 阶对称矩阵 A 进行压缩存储,若 B 中只存储对称矩阵 A 的下三角元素,则A[i,j](i<j,0≤i,j≤n−1)存储在 B 中对应的元素为( )。
A. B[j∗n/2+i]
B. B[i∗(i+1)/2+j]
C. B[j∗(j+1)/2+i]
D. B[i∗n/2+j]1.参考答案:C
解析:因题目要求存储的是下三角矩阵,对于i<j,该位置对应的是上三角的某个元素,实际上存储位置是对应的下三角矩阵上的(j,i)。那么先求元素(j,i)所在行之前所有元素个数,即j(j+1)/2,然后加上i即是最终位置。2.下三角矩阵A(n×n)按列优先顺序压缩在数组S[(n+1)∗n/2]中,若非零元素aij(0≤i,j<n)存放在S[k]中,则i,j,k的关系为( )。
A. k=i∗n+j
B. k=(2n−j+1)∗j/2+i−1
C. k=(i+1)∗i/2+j
D. k=(2n−j+1)∗j/2+i−j2.参考答案:D
解析:同上,只是换成列优先,到第j列之前存放了n+(n−1)+⋯+(n−j+1)=(2n−j+1)×j/2个元素,后加上第i行距离对角线上的元素(j,j)的偏移i−j可得答案。3.若将6×6的上三角矩阵 A(下标从 1 起)的上三角元素按行优先存储在一维数组 b 中,且b[1]=A11,那么A35在 b 的下标是( )。
A. 12
B. 13
C. 14
D. 153.参考答案:C
解析:上三角矩阵第 1 行 6 个元素,第 2 行 5 个,以此类推,A35是第 3 行的第 3 个元素,因此答案为6+5+3=14。4.稀疏矩阵的压缩存储缺点在于( )。
A. 无法得到矩阵的维数信息
B. 无法根据行列号查找矩阵元素
C. 无法随机存取
D. 使矩阵的逻辑关系变得更复杂4.参考答案:C
解析:将稀疏矩阵压缩存储之后就无法进行随机存取,需要遍历三元组或其他存储结构才可以获得元素信息。5.若以行优先顺序存储三维数组A[80][20][40],其中元素A[0][0][0]所在地址为 0,且每个元素占 4 个存储单元,则A[20][10][30]的地址为( )。
A. 65720
B. 65724
C. 65716
D. 657285.参考答案:A
解析:数组 A 可以看作高 80,行 20,列 40 的立方体。则 20,10,30 是第20×(20×40)+10×40+30=16430个元素(含第 0 个元素),每个元素占 4 个存储单元,则地址为16430×4=65720。
4.4.4 真题演练
6.【2016】有一个 100 阶的三对角矩阵 M,其元素mi,j(1≤i≤100,1≤j≤100)按行优先次序压缩存入下标从 0 开始的一维数组 N 中。元素m30,30在 N 中的下标是( )。
A. 86
B. 87
C. 88
D. 896.参考答案:B
解析:带入三对角矩阵的计算公式即可得2×30+30−3=87。也可按照本节中的推导过程进行逐行计算。7.【2017】适用于压缩存储稀疏矩阵的两种存储结构是( )。
A. 三元组表和十字链表
B. 三元组表和邻接矩阵
C. 十字链表和二叉链表
D. 邻接矩阵和十字链表7.参考答案:A
解析:三元组主要用于存储稀疏矩阵,十字链表用于存储图,此处可将稀疏矩阵视为图。邻接矩阵需要n2的空间存储矩阵,开销过大,而二叉链表用于存储树或森林。8.【2018】设有一个12×12的对称矩阵 M,将其上三角部分的元素mi,j(1≤i≤j≤12)按行优先存入 C 语言的一维数组 N 中,元素m6,6在 N 中的下标是( )。
A. 50
B. 51
C. 55
D. 668.参考答案:A
解析:按行优先存储上三角部分,前 5 行共存12+11+10+9+8=50个元素,m6,6是第 6 行第一个需要存的元素,数组下标从 0 开始,因此50+1−1=50。或代入书中所给公式即得(6−1)×(2×12−6+2)/2+6−6=50。9.【2020】将一个10×10对称矩阵 M 的上三角部分的元素mi,j(1≤i≤j≤10)按列优先存入 C 语言的一维数组 N 中,元素m7,2在 N 中的下标是( )。
A. 15
B. 16
C. 22
D. 239.参考答案:C
解析:按列优先存储上三角部分,第 1 列有 1 个元素,第 2 列 2 个… 到第 6 列 6 个,总共 21 个元素,因此m7,2对应元素m2,7是第21+2=23个元素,又因为数字下标从 0 开始,则减一为 22。10.【2021】已知二维数组 A 按行优先方法存储,每个元素占用 1 个存储单元,若元素A[0][0]的存储地址为 100,A[3][3]的存储地址为 220,则元素A[5][5]的存储地址是( )。
A. 295
B. 300
C. 301
D. 30610.参考答案:B
解析:A[3][3]的存储地址为 220,则A[3][0]的存储地址为 217,又因为A[0][0]的存储地址为 100,可得数组中一行元素占用 39 个存储单元,因此A[5][0]的存储地址为217+2×39=295,A[5][5]的存储地址为 300。4.5 章末总结
(1) 栈与队列是在线性表的基础上,对操作进行了限制而得到的数据结构,是一种特殊的线性表。很多内容可以和线性表进行对比学习,从而理解什么叫做 “操作受限的线性表”。
(2) 线性表的物理结构可以采取顺序存储或链式存储的方式来实现,因此栈与队列也可以采取这两种方式来实现。栈与队列的出入操作与其实现方式有关,需要对 “栈顶指针”、“队首指针” 以及 “队尾指针” 进行操作并插入和删除数据。
(3) 本章虽然先讲解了栈与队列的结构,随后才讲解栈与队列的应用,但数据结构的存在是为了解决问题的,先有实际问题,后有解决该问题的数据结构。正是因为缓冲区需要有 “先进先出” 和 “暂存” 的特点,才有了 “先进先出” 的队列。考生在做题时,尤其是算法大题中需要设计数据结构解决问题时,应首先判断该实际问题用什么样的数据结构最方便。对于需要 “后进先出” 的问题,如遍历迷宫地图时,若选择了错误的道路则需要逐步返回,就应该采用栈来实现。而判断回文句,需要从两端各取一个字母进行比较,直到中间位置比较结束,就应该使用可以在两端进行输出操作的双端队列。
(4) 栈与队列的出入操作是 408 中重点且频繁考查的部分,需要在纸上进行插入删除的模拟以得出答案,因此需要非常熟悉栈与队列的插入删除操作,即出栈入栈、出队入队。
(5) 对于压缩矩阵的部分,真题频繁考查下标的计算过程。这需要通过找规律得出答案,在进行公式计算时,可以从 “第i行之前总共有多少个元素” 入手,这样就可以得出aij所存放位置的数组下标。需要注意题中给出用于存储的数组下标是从 0 还是从 1 开始计算。表 4.4 栈与队列总结
存取特点
判空条件
判满条件
应用
顺序栈
LIFO
top == -1
top == MAX_SIZE - 1
递归,表达式求解,表达式转化,括号匹配,迷宫求解,进制转化等
链栈
LIFO
top == NULL
无
循环队列
FIFO
front == rear
(rear + 1) % MAX_SIZE == front
缓冲区,消息队列,迷宫求解等
链队列
FIFO
front == rear
无
卡特兰数和合法出入栈序列问题
1.若有n个不同的元素进栈,则对应的出栈方案有多少种?
若进栈序列为1,2,3,⋯,n,用函数f(n)表示可能的出栈序列种数。当n=0时,f(0)=1,出栈序列为{};当n=1时,f(1)=1,出栈序列为{1};当n=2时,f(2)=2,出栈序列中若 1 在首位,则 1 左侧有 0 个数,1 右侧有 1 个数,对应f(0)×f(1)种可能;若 1 在末位,1 左侧有一个数,右侧有 0 个数,对应f(1)×f(0)种可能。此时共有f(0)×f(1)+f(1)×f(0)种序列。
依次类推,将i置于i=1,2,3,⋯,n处,可能的序列种数为:f(i−1)×f(n−i)。则f(n)=f(0)×f(n−1)+f(1)×f(n−2)+⋯+f(n−1)×f(0)=种(卡特兰数)。
2. 不可能的出栈序列特征是什么?
设下标i<j,若进栈模式是pi⋯,pj,pj+1,则pj+1⋯,pi⋯,pj是不可能的出栈模式。即出栈序列中当前下标大于后续的一系列下标S时,则这些下标S的出栈序列必定是递减的。
例如入栈序列是p0,p1,p2,p3,出栈时p0,p3先弹出,此时p3下标大于后续未出现的p1,p2,则它们必定按下标递减顺序p2,p1出现。3. 如何快速判断一个出栈序列 PopOpSeq 是否是给定的入栈序列 PushOpSeq 的出栈序列?
借助一个栈st进行判断。若 PushOpSeq 和 PopOpSeq 是有效的栈操作序列,则经过所有的入栈和出栈操作后,每个元素各入栈和出栈一次,栈st必定为空。具体方法用代码讲解:
bool judgePopOpSeq(char PushOpSeq[], char PopOpSeq[]) { SqStack st; initialize(st); // 定义一个栈并初始化 int n = strlen(PushOpSeq); j = 0; // j是当前需要执行的出栈操作的下标 for (int i = 0, j = 0; i < n; ++i) { push(st, PushOpSeq[i]); // 入栈操作 // 栈顶元素和当前PopOpSeq内元素相等,进行出栈操作 while (!stackEmpty(st) && st.top() == PopOpSeq[j]) { st.pop(); ++j; // 出栈操作 } } return stackEmpty(st); // 若栈为空,则PopOpSeq是PushOpSeq的出栈序列 }该方法基于贪心,时间复杂度仅O(n)。
数据结构第4章 栈、队列和数组 (竟成)
news2026/2/16 3:00:35
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2392525.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
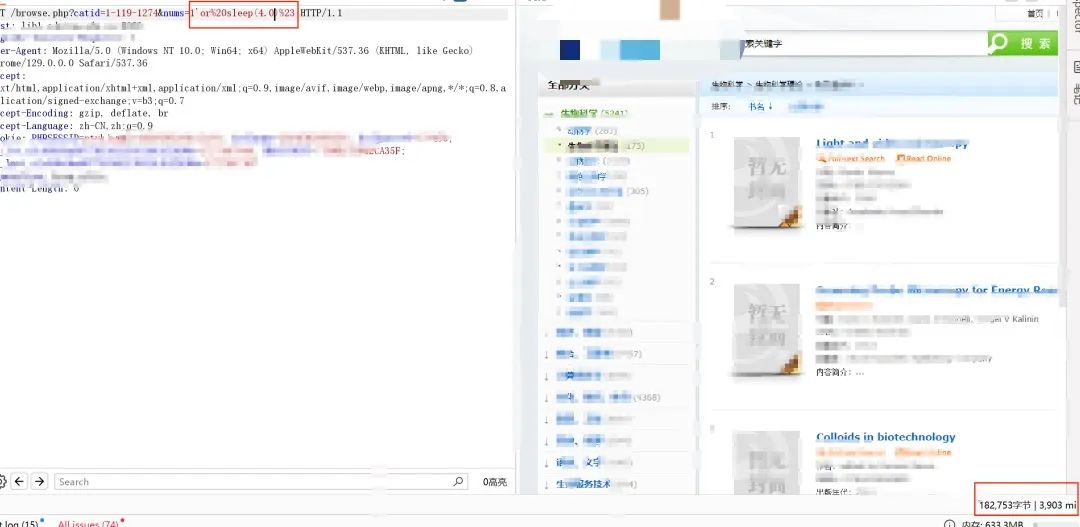
2025年渗透测试面试题总结-匿名[校招]安全研究员(SAST方向)(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。
目录 匿名[校招]安全研究员(SAST方向)
一面问题回答框架
1. 自我介绍
2. 简历深挖(漏洞挖掘&#x…
Unity 游戏优化(持续更新中...)
垃圾回收 是什么? 垃圾回收(Garbage Collection)GC 工作机制 1、Unity 为用户生成的代码和脚本采用了自动内存管理。 2、小块数据(如值类型的局部变量)分配在栈上。大块数据和长期存储分配在托管堆上。 3、垃圾收集…
20250529-C#知识:索引器
C#知识:索引器 索引器给对象添加了索引访问的功能,实际访问的是对象的成员,感觉不太常用。 1、主要内容及代码示例
索引器中类似属性,也包含get和set方法索引器能够使像访问数组一样访问对象一般当类中有数组类型的成员变量时&am…
【笔记】suna部署之获取 Tavily API key
#工作记录 Tavily 注册 Tavily 账号5: 打开浏览器,访问 Tavily 官网Tavily AI。点击页面上的 “注册” 按钮,按照提示填写注册信息,如邮箱地址、设置密码等,完成注册流程。也可以选择使用 Google 或 GitHub 账号授权登…
06-Web后端基础(java操作数据库)
1. 前言
在前面我们学习MySQL数据库时,都是利用图形化客户端工具(如:idea、datagrip),来操作数据库的。
我们做为后端程序开发人员,通常会使用Java程序来完成对数据库的操作。Java程序操作数据库的技术呢,有很多啊&a…
Ubuntu的shell脚本
关于shell脚本 • shell脚本是文本的一种。 • shell脚本是可以运行的文本。 • shell脚本的内容是由说辑和数据组成。 • shell 脚本是解释型语言。 shell脚本存在的意义 Shell脚本语言是实现Linux/UNIX系统管理及自动化运维所必备的重要工具 Linux/UNIX系统…
从抄表到节能,电费管理系统如何重构公寓运营场景——仙盟创梦IDE
租房公寓电费管理系统是集智能计量、自动化计费、线上缴费、数据管理于一体的综合性解决方案,旨在解决传统电费管理中人工抄表误差大、收费效率低、纠纷频发等痛点。系统通过部署智能电表实时采集用电数据,结合云计算与大数据分析技术,实现电…
记一次前端逻辑绕过登录到内网挖掘
前言
在测试一个学校网站的时候,发现一个未授权访问内网系统,但是这个未授权并不是接口啥的,而是对前端 js 的审计和调试发现的漏洞,这里给大家分享一下这次的漏洞的过程。
进入内网的过程 可以看到是一个图书馆的网站ÿ…
Springboot 整合 WebSocket 实现聊天室功能
目录 前言一、WebSocket原理二、Spring Boot集成WebSocket2.1. 引入依赖2.2 配置类WebSocketConfig2.3 WebSocketServer 类2.4 前端代码 index.html2.5 Controller访问首页 前言
WebSocket概述: 在日常的web应用开发中,常见的是前端向后端发起请求&…
用 Trae IDE 打造一个桌面小爬虫:从 PyQt5 开始,轻松采集掘金首页内容
很多程序员都有这样的经历:刷掘金、看文章、找灵感、追热点。但你有没有想过,有一天让“爬虫”代替你去浏览这些内容?自动提取标题、作者、点赞数、评论数,一键生成你的专属“技术热点日报”。
今天我们就用 Trae IDE PyQt5 来完…
python和风api获取天气(JSON Web Token)
下载安装openssl 默认安装目录,添加C:\Program Files\OpenSSL-Win64\bin到用户Path环境变量 打开cmd,执行命令,会生成两个文件ed25519-private.pem,ed25519-public.pem
openssl genpkey -algorithm ED25519 -out ed25519-privat…
52、C# 泛型 (Generics)
泛型是 C# 2.0 引入的一项强大功能,它允许你编写可以处理多种数据类型的代码,而无需为每种类型重复编写相同的逻辑。泛型提高了代码的重用性、类型安全性和性能。
基本概念
泛型类
public class GenericClass<T>
{private T _value;public Gene…
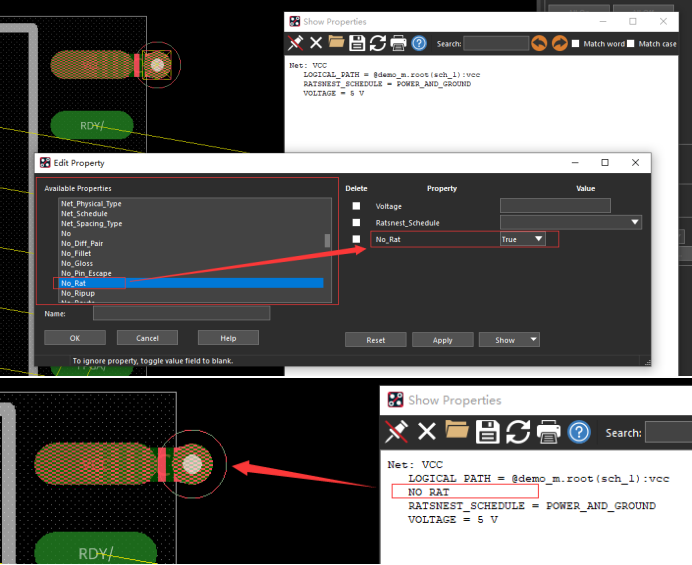
Allegro X PCB设计小诀窍--05.如何在Allegro X中实现隐藏电源飞线效果
背景介绍:在PCB设计过程中,布线初期印制板上的飞线错综复杂,信号线和电源线混合交错,但是实际上对于多层板来说,电源的网络一般是通过电源层铺铜连接的,很少需要走线,这样混乱的情况会严重影响设…
一篇文章教会你ESP8266串口WIFI无线模块实现物联网无线收发,附STM32代码示例
目录 一、ESP-01S无线模块:
(1)特点: (2)管脚定义:
(3)启动模式: 二、ESP-01S出厂固件烧录:
(1)引脚接线:
࿰…
Reactor模式详解:高并发场景下的事件驱动架构
文章目录 前言一、Reactor模式核心思想二、工作流程详解2.1 服务初始化阶段2.2 主事件循环2.3 子Reactor注册流程2.4 IO事件处理时序2.5 关键设计要点 三、关键实现技术四、实际应用案例总结 前言
在现代高性能服务器开发中,如何高效处理成千上万的并发连接是一个关…
项目日记 -Qt音乐播放器 -设置任务栏图标与托盘图标
博客主页:【夜泉_ly】 本文专栏:【Qt音乐播放器】 欢迎点赞👍收藏⭐关注❤️ 代码仓库:MusicPlayer v1.0版视频展示:Qt -音乐播放器(仿网易云)V1.0
前言
本文的目标: 一是设置任务栏的图标, 二…
国产 BIM 软件万翼斗拱的技术突破与现实差距 —— 在创新与迭代中寻找破局之路
万翼斗拱在国产BIM领域迈出重要一步,凭借二三维一体化、参数化建模及AI辅助设计等功能形成差异化竞争力,在住宅设计场景中展现效率优势,但与国际主流软件相比,在功能完整性、性能稳定性和生态成熟度上仍有显著差距,需通…
Golang|etcd服务注册与发现 策略模式
etcd 是一个开源的 分布式键值存储系统(Key-Value Store),主要用于配置共享和服务发现。 ETCD是一个键值(KV)数据库,类似于Redis,支持分布式集群。ETCD也可以看作是一个分布式文件系统ÿ…































![2025年渗透测试面试题总结-匿名[校招]安全研究员(SAST方向)(题目+回答)](https://i-blog.csdnimg.cn/direct/2ea6508e11f348769528e86055da4fc5.png)