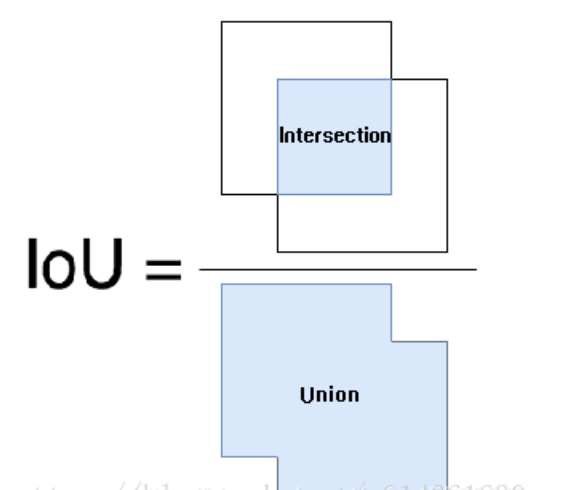
一维iou

二维

import numpy as np



def iou_1d(set_a, set_b):

	# 获得集合A和B的边界 
	x1, x2 = set_a
	y1, y2 = set_b
	# 计算交集的上下界
	low = max(x1,y1)
	high - min(x2, y2)
	# 计算交集
	if high - low < 0:
		inter = 0
	else:
		inter = high - low
	# 计算并集
	union = (x2 -x1) + (y2 - y1) - inter
	# 计算IoU
	iou = inter / union
	return iou


def iou_2d(box1,box2):
	'''
	二维IoU的计算：
	注意图像坐标系的原点一般在左上角，x方向朝右，y方向朝下
	box的表示:[top, left, bottom, right]
	box的表示分别对应:[y1,x1,y2,x2]
	'''
	in_h = min(box1[2],box2[2]) - max(box1[0],box2[0])
	in_w = min(box1[3],box2[3]) - max(box1[1],box2[1])
	inter = 0 if in_h  < 0 or in_w < 0 else in_h * in_w
	union = (box1[2] - box1[0]) * (box1[3] - box1[1]) +  (box2[2] - box2[0]) * (box2[3] - box2[1])  - inter
	iou = inter / union
	return iou


def  iou_3d(box1,box2):
	'''
	3D IoU计算
	box表示形式：[x1,y1,z1,x2,y2,z2] 分别是两对角点的坐标
	'''
	in_w = min(box1[3],box2[3]) - max(box1[0],box2[0])
	in_l = min(box1[4],box2[4]) - max(box1[1],box2[1])
	in_h = min(box1[5],box2[5]) - max(box1[2],box2[2])

	inter = 0 if in_w < 0 or in_l < 0 or in_h < 0 else in_w * in_l * in_h
	union = (box1[3] - box1[0]) * (box1[4] - box1[1]) * (box1[5] - box1[2]) + (box2[3] - box2[0]) * (box2[4] - box2[1]) * (box2[5] - box2[2])  - inter
	iou = inter / union
	return iou


if __name__ == '__main__':
	box1 = [0,0,0,1,1,1]
	box2 = [0.5,0.5,0.5,1.5,1.5,1.5]
	print(iou_3d(box1,box2))