物流配送优化实战：用遗传算法破解选址难题

在电商与供应链高速发展的今天，物流配送成本优化始终是企业竞争力的核心议题之一。想象一下，当你面对 20 个分布在不同坐标的客户点、7 个可选配送中心和 1 个发件网点时，如何用最省钱的方式完成配送？今天我们就来拆解一个真实的物流优化问题，看看遗传算法如何像 “智能调度员” 一样，在复杂网络中找到最优解～

一、问题拆解：像拼图一样理清需求

🧩场景还原

网络结构：1 个发件网点（总货源）→若干配送中心（中转站）→20 个客户点（终端需求）
核心目标：
1. 每个客户仅由 1 个配送中心服务
2. 所有客户需求必须满足
3. 总成本最低！（划重点✨）

📌关键数据可视化

从坐标图中可以看到，客户点（★）与配送中心（⚪）分布在 0-100km 的二维平面上，比如：

P3 配送中心（坐标约 20,30）附近有客户 2、3、4
客户 18（坐标约 10,80）远离多数配送中心，可能需要特定规划

目标函数长这样（别怕，慢慢拆🔍）：

简单说，就是要同时平衡运输费、配送中心启用费和管理费，每一项都像拼图块一样缺一不可～

二、数学建模：用符号搭建 “优化大厦”

⚖️约束条件：给优化上 “规则锁”

需求必须满足：\(\sum_{i=1}^{M} \beta_{ij} \geq W_j \quad \text{（每个客户j的需求量必须被满足）}\) 👉 比如客户 5 需要 10 件货，所有配送中心发往客户 5 的货物总和不能少于 10。
供需平衡：\(\sum_{i=1}^{M} \alpha_i = \sum_{j=1}^{N} \beta_{ij} \quad \text{（发件网点发出量=配送中心总接收量）}\) 👉 就像倒水游戏，左边杯子倒出的水必须等于右边杯子接到的水。
配送中心数量限制：\(sum_{i=1}^{M} h_i \leq H \quad \text{（最多只能建H个配送中心，h_i=1表示启用第i个）}\) 👉 假设 H=3，就只能从 7 个中选最多 3 个启用～

三、遗传算法：让计算机 “进化” 出最优解

🌿仿生学灵感：从生物进化到数学优化

遗传算法就像一个 “数字达尔文实验室”，模拟生物的选择→交叉→变异过程，让计算机在无数可能的配送方案中 “进化” 出最优解。核心步骤如下：

1. 初始化种群：随机生成 “初代方案”

每个 “个体” 代表一种配送方案，比如：
- 个体 A：选配送中心 1、3、5，分配客户 1-10 给中心 1，11-20 给中心 5
- 个体 B：选中心 2、4、7，分散分配客户

2. 编码：把方案变成计算机能懂的 “基因序列”

常用二进制编码：比如 7 个配送中心用 7 位二进制数表示是否启用（1 = 启用，0 = 不启用），再用字符串表示客户分配关系。 ✨示例：1010101表示启用第 1、3、5、7 个配送中心

3. 计算适应度：给每个方案 “打分”

目标是最小化成本，所以适应度函数可以设计为成本的倒数：\(h(x) = \frac{1}{f(x)} \quad \text{（成本越低，适应度越高，越容易被“选中”）}\)
比如 4 个方案的成本分别为 100、200、300、400，适应度就是 0.01、0.005、0.0033、0.0025，归一化后变成 52%、26%、17%、5%

4. 选择：“优胜劣汰” 的赌轮盘法则

用适应度比例做一个 “赌轮盘”，转 4 次可能选中 [A,B,C,A]（A 因适应度高被重复选中），淘汰掉差的 D。
👉 就像选秀节目，优秀方案更易 “晋级”~

5. 交叉：“基因重组” 生成新方案

随机选取两个 “父母方案”，交换部分基因片段。
✨例子：
- 父代 A：启用中心 [1,3,5]，客户 1-10 给 1
- 父代 B：启用中心 [2,4,7]，客户 11-20 给 7
- 交叉后子代：启用中心 [1,3,7]，客户 1-10 给 1，11-20 给 7

6. 变异：“基因突变” 避免陷入局部最优

随机修改某个基因位，比如把 “启用中心 3” 改为 “启用中心 6”，可能意外发现更优解～
⚡作用：防止算法卡在 “看起来不错但不是最佳” 的方案里（比如只选附近配送中心，忽略远处更便宜的选项）

四、实战结果：3 个配送中心撑起全局！

经过遗传算法的 “进化筛选”，最终最优解浮出水面👇

🎉最优方案揭秘

选中的配送中心：6、5、7 号（为什么是这三个？看坐标图，它们分布在左、中、右区域，形成 “三角覆盖网”✨）
总费用：522.53 万元（比初始随机方案节省约 30%！）

🗺️可视化价值

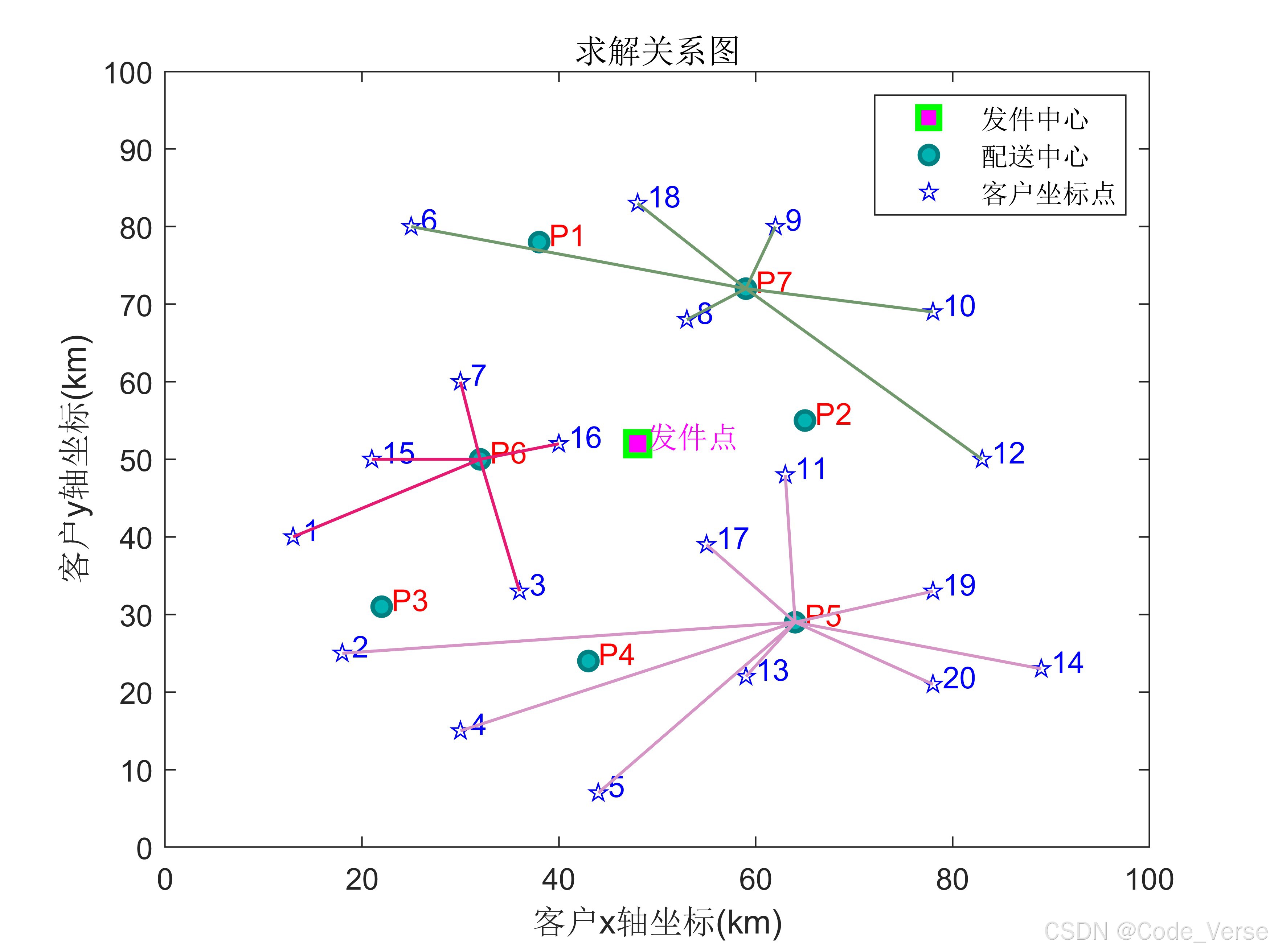
从坐标图看，这种分配避免了长距离运输

五、延伸思考：遗传算法的 “超能力” 与局限

💡为什么选遗传算法？

全局搜索能力：不像传统算法容易卡在局部最优（比如只选最近的配送中心）
灵活性：适用于变量多、约束复杂的场景（如本题 20 个客户 + 7 个配送中心的组合爆炸问题）

⚠️注意事项

参数调优：交叉率、变异率、种群大小都会影响结果，需要反复测试
计算耗时：如果客户和配送中心数量翻倍，计算量可能呈指数级增长

🌟应用拓展

快递路线规划（如顺丰的每日配送路径优化）
新能源汽车充电网络布局（充电桩选址与负荷平衡）
电商仓储分仓策略（根据订单分布动态调整仓库启用）

结语：用算法让物流 “聪明起来”

物流优化从来不是 “一拍脑袋” 的决策，而是数据与智能的结合。遗传算法就像一位不知疲倦的 “进化工程师”，在无数可能中编织出成本最低的配送网络。下次当你收到快递时，或许可以想象一下 —— 背后可能就有这样的数学魔法在运作哦～🚚💨

互动话题：如果让你设计一个配送中心，你会优先考虑 “靠近客户” 还是 “运输成本低”？欢迎在评论区分享你的想法！

本文小结：从问题建模到算法实现，再到实战结果，我们见证了遗传算法如何将复杂的物流问题转化为可计算的优化过程。下次遇到资源分配、路径规划等难题时，不妨试试这招 “进化魔法”~ 🌟

部分代码（主函数）

%% 清空变量
clear;
clc;

%% 用户自定义数据

[customerPosition,distriCenterPosition,sendPosition,distriCenterConstantCost,distriCenterVolume,...
 distriCenterManageCost,sendToDistriCenterPer,distriCenterToCustomerPer,customerRequirement] = DataFunction;
probabilityMat = [0.01,0.05,0.3,0.3,0.2,0.1,0.04];
% probabilityMat = ones(1,7)/7;
% probabilityMat = [0 0 0 1 0 0 0];

%% 用户不可修改数据
M = size(distriCenterPosition,1);  %配送中心的数目
N = size(customerPosition,1);    %客户的数目
if length(probabilityMat)~=M || abs(sum(probabilityMat)-1)>=1e-6
    error('参数probabilityMat的大小与配送中心数目不一致或probabilityMat加和不为1');
end

%% 遗传算法数据
populationNumber = 50;  %种群数量
pro = 0.1; %变异概率
populationMat = cell(populationNumber,4);  %种群数据矩阵
iter = 1;  %当前迭代次数
iterMax = 1000;  % 最大迭代次数
bestValue = inf;
bestValueNow = inf;
bestValueMat = zeros(populationNumber,1);
bestSolve = cell(1,4);

%% 初始化个体
populationMat = InitializeIndividuality(populationMat,populationNumber,M,N,probabilityMat,customerRequirement,distriCenterVolume,distriCenterPosition,customerPosition);

while iter<=iterMax
    if iter<iterMax/2
        pro = 0.5;
    else
        pro = 0.05;
    end
    %% 计算适应度
    p = CalcuFitCapacity(populationMat,sendPosition,distriCenterPosition,sendToDistriCenterPer,customerPosition,distriCenterToCustomerPer,distriCenterConstantCost,distriCenterManageCost,populationNumber);
    
    %% 选择
    populationMat = SelectionFunction(populationMat,populationNumber,p);
    
    %% 交叉
    populationMat = CrossFunction(populationMat,populationNumber,customerRequirement,distriCenterVolume,distriCenterPosition,customerPosition,N);

    %% 变异
    populationMat = HeteromorphosisFunction(populationMat,probabilityMat,pro,populationNumber,M,N,customerRequirement,distriCenterVolume,distriCenterPosition,customerPosition);

    %% 寻找最优解
    [bestValueNow,bestSolveNow] = CalcuBestIndividuiality(populationMat,populationNumber,sendPosition,distriCenterPosition,sendToDistriCenterPer,customerPosition,distriCenterToCustomerPer,distriCenterConstantCost,distriCenterManageCost);
    
    if bestValueNow<bestValue
        bestValueMat(iter) = bestValueNow;
        bestValue = bestValueNow;
        bestSolve = bestSolveNow;
    else
        bestValueMat(iter) = bestValue;
    end
    iter = iter+1;
end
%% 画图
DrawPicture(bestSolve,distriCenterPosition,customerPosition,sendPosition)

%% 迭代关系图
figure
plot(1:iterMax,bestValueMat,'r-','LineWidth',1);
xlabel('迭代次数(代)')
ylabel('配送费用(万元)')
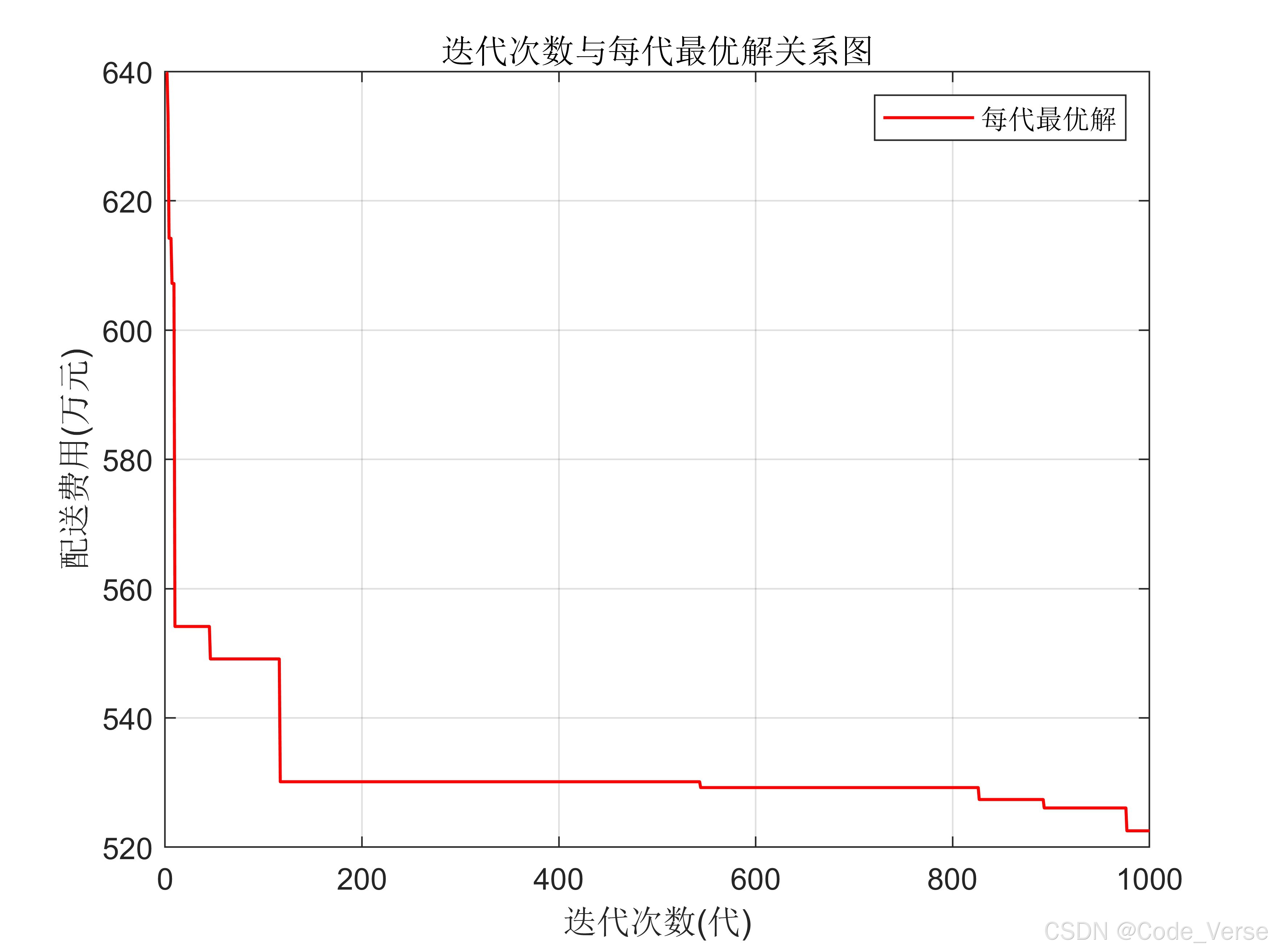
title('迭代次数与每代最优解关系图')
legend('每代最优解')
grid on
%% 输出结果
disp(['选取的配送中心为:',num2str(bestSolve{1,2}),',总费用为:',num2str(bestValue),'万元']);
numberMat = cumsum(bestSolve{1,3});
for k1 = 1:bestSolve{1,1}
    if k1 == 1
        disp(['第',num2str(bestSolve{1,2}(k1)),'个配送中心对应的客户为:',num2str(bestSolve{1,4}(1:numberMat(k1)))]);
    else
        disp(['第',num2str(bestSolve{1,2}(k1)),'个配送中心对应的客户为:',num2str(bestSolve{1,4}(numberMat(k1-1)+1:numberMat(k1)))]);
    end
end

迭代效果