5月26日复盘
一、自注意力机制
Self-Attention Mechanism,自注意力机制,用于捕捉序列数据内部依赖关系的关键技术。它在NLP和CV中非常重要,尤其是Transformer。
1. 产生背景
自注意力机制的产生与序列建模任务(如机器翻译、文本生成等)中的挑战密切相关,比如RNN、LSTM等在处理长序列时有梯度消失(或爆炸)、计算效率低、难以并行化等诸多局限性。
1.1 认识seq2seq
Seq2Seq(Sequence-to-Sequence)是NLP中的经典框架,广泛应用于机器翻译、文本摘要等。其结构包括:
- Encoder:编码器,将输入序列编码为一个固定长度的上下文向量。
- Decoder:解码器,基于上下文向量生成输出序列。

1.2 提出问题
在自注意力机制之前,序列建模任务主要依赖于以下模型:
- RNN:循环神经网络,能够处理序列数据,但存在梯度消失/爆炸问题,难以捕捉长距离依赖。
- LSTM/GRU:通过门控机制缓解了RNN的问题,但处理长序列时难以并行化,计算效率低。
共同问题是:
- 长距离依赖:随着序列长度增加,模型难以有效捕捉远距离元素之间的关系。
- 计算效率:需要逐步处理序列,无法并行计算,训练速度较慢。
- 信息瓶颈:编码器会将整个输入序列压缩为一个固定长度的向量,可能导致信息丢失,灵活度太低。
1.3 解决问题
一开始选择的是CNN的思想,但是CNN要堆叠很多层,于是就出现了自注意力机制。
1.3.1 解决并行化
使用CNN解决并行化问题。问题及解决对比:

CNN 证明了并行化在序列建模中的可行性,并为后续模型(如 Transformer)提供了灵感。
1.3.2 引入自注意力机制
为了综合解决上述各种问题,提出了自注意力机制,并在Transformer中得到了广泛应用。其核心思想是:

- 长距离依赖捕获:通过计算序列中每个元素与其他元素的相关性,捕捉全局依赖关系。
- 并行计算:不依赖序列顺序,可并行处理整个序列,显著提高计算效率。
- 动态权重分配:模型可以动态地关注序列中不同位置的重要信息,不再依赖固定的上下文向量。
- 灵活性:可以处理不同长度的输入序列,不像卷积或RNN那样对输入的结构有严格要求。
1.4 使用场景
语言的含义是极度依赖上下文,同一个词或句子在不同的上下文中可能会有完全不同的含义。比如:货拉拉拉不拉拉布拉多要看拉布拉多在货拉拉上拉不拉baba~
比如下面这个机器人第二法则:
机器人第二法则
机器人必须遵守人类给它的命令,除非该命令违背了第一法则。
要想理解或处理句子中高亮的三个词语,那就必须和上下文联系起来。当模型处理这句话的时候,它必须知道:
- 「它」指代机器人
- 「命令」指代前半句话中人类给机器人下的命令,即「人类给它的命令」
- 「第一法则」指机器人第一法则的完整内容。
那么,此时我们就需要使用自注意力机制来理解上下文。
1.5 基本概念
自注意力机制,就是找到自己和所在句子的所有的词之间的关联关系。
1.5.1 核心目标
 |
|---|
| 我是谁?我在哪? |
自注意力的目标是让每个位置的表示能够根据整个序列中其他位置的信息进行加权融合,从而捕获实体之间的相互关系。
自注意力机制是要回答:“我(某个位置)应该关注谁(其他位置)?以及关注了之后该怎么融合信息?”
1.5.2 专业术语
我是华清远见的一名AI老师;
为了提升表达能力和灵活度,我们不能直接使用一个词嵌入向量。
自注意力机制通过引入查询向量(Query)、键向量(Key)、**值向量(Value)**概念来实现序列中各元素之间的信息交互和依赖建模。
-
Q:Query
表示当前查询者的位置,用来发出问题:“我想知道对我来说谁重要”。
-
K:Key
表示被查询者的身份,是所有位置给出的“介绍信”或“标签”,告诉别人自己是个啥玩意。
-
V:Value
表示被查询者实际信息,也就是一旦你决定“关注我了”,我就把这份信息给你。
1.5.3 QKV的意义
序列中的每个 T o k e n Token Token 都有 Q 、 K 、 V Q、K、V Q、K、V 三个角色:
- 所有位置之间需要【查询-响应】这样的互动,单一角色表达能力就太死板。
- “我该关注谁”是“我”和“他们”之间的交互过程,所以需要把“我”和“他们”分别建模(Q vs K)。
- 而最终融合的信息
V
V
V 可能和你打分
Q
⋅
K
Q·K
Q⋅K 的依据不完全相同,如:
- K K K :强调结构特征→【位置或语法角色】
- V V V: 强调语义内容→【单词的意义】
2. 实现过程
自注意力机制通过计算输入数据中每个位置与其他位置的相关性,来调整每个位置的信息表示。
2.1 输入序列
输入是一个序列,如词向量序列,假设:
X
=
(
x
1
,
x
2
,
…
,
x
n
)
∈
R
n
×
d
X = (x_1, x_2, \dots, x_n) \in \mathbb{R}^{n \times d}
X=(x1,x2,…,xn)∈Rn×d
是
n
n
n 个输入,
d
d
d 是输入维度,则自注意力的目的是捕获
n
n
n 个实体之间的关系。
2.2 词语关系
it代表的是animal还是street呢,对我们来说简单,但对机器来说是很难判断的。self-attention就能够让机器把it和animal联系起来。

2.3 线性变换
自注意力机制依赖于三个核心概念:查询向量Query、键向量Key、值向量Value。他们对输入 X X X 进行三次线性变换,得到三个矩阵。

2.3.1 查询向量
Q = Query, 是自注意力机制中的“询问者”。每个输入都会生成一个查询向量,表示当前词的需求。
- 作用:用于与键向量计算相似度(通过点积方式),确定当前词与其他词的相关性。
- 生成方式:通过一个权重矩阵将输入数据(如词向量)映射到查询空间。
Q = X W q Q=X W_q Q=XWq
W q W_q Wq 是可学习权重矩阵,维度为 d × d k d \times d_k d×dk, d k d_k dk是超参数,表示查询向量的维度。
代码参考如下:
# 随机生成自注意力机制的Query映射的权重矩阵
Wq = torch.randn(512, 512)
Query = torch.matmul(embedding_out, Wq)
print(Query.shape) # torch.Size([7, 512])
注:映射后维度保持不变可以简化模型设计
2.3.2 键向量
**K = **Key,表示其他词的信息,供查询向量匹配。每个输入都会生成一个键向量,表示其能够提供的信息内容。
- 作用:与查询向量计算点积,生成注意力权重。点积越大,表示它们之间的相关性越强。
- 生成方式:通过一个权重矩阵将输入数据(如词向量)映射到键空间。
K = X W k K=X W_k K=XWk
W k W_k Wk 是可学习权重矩阵,维度为 d × d k d \times d_k d×dk, d k d_k dk是超参数,表示键向量的维度。
代码参考如下:
# 随机生成自注意力机制的Key映射的权重矩阵
Wk = torch.randn(512, 512)
Key = torch.matmul(embedding_out, Wk)
print(Key.shape) # torch.Size([7, 512])
注:映射后维度保持不变可以简化模型设计
2.3.3 值向量
V = Value, 值向量包含了每个输入实际的信息内容,相关性决定了信息被聚焦的程度。
- 作用:使用值向量基于注意力得分进行加权求和,生成最终的输出表示。
- 生成方式:通过一个权重矩阵将输入数据(如词向量)映射到值空间。
V = X W v V=X W_v V=XWv
W v W_v Wv 是可学习权重矩阵,维度为 d × d v d \times d_v d×dv, d v d_v dv是超参数,表示值向量的维度。
代码参考如下:
# 随机生成自注意力机制的Value映射的权重矩阵
Wv = torch.randn(512, 512)
Value = torch.matmul(embedding_out, Wv)
print(Value.shape)
注: d v d_v dv 和 d k d_k dk 通常是相等的。
2.3.4 以图示意
通过线性变换得到三个向量的变化如下图所示:

2.4 注意力得分
使用点积来计算查询向量和键向量之间的相似度,除以缩放因子
d
k
\sqrt{d_k}
dk 来避免数值过大,使得梯度稳定更新。得到注意力得分矩阵:
Attention
(
Q
,
K
)
=
Q
K
T
d
k
\text{Attention}(Q, K) = \frac{QK^T}{\sqrt{d_k}}
Attention(Q,K)=dkQKT
参考代码如下:
# 计算原始的注意力得分
score = torch.matmul(Query, Key.transpose(0, 1)) / math.sqrt(512)
print(score)
输出:
tensor([[ -178.6881, 1285.5822, 495.5278, -599.9384, -384.6758, -477.1410, 131.7539],
[ -186.2839, 687.4478, 683.4026, -480.1666, -681.2383, 483.9817, 135.0674],
[ 629.8547, -542.7538, 920.4750, 120.9331, -649.9722, -1237.3368, -483.4400],
[ -95.6489, 825.4144, 410.6800, 353.1750, -582.8438, 6.5602, 766.4843],
[ -91.9296, 830.8030, -100.2955, 12.4473, 393.9949, -378.9345, -156.0786],
[ 901.4327, -277.5199, -1051.5514, -309.8069, 557.1041, 386.2509, 132.9100],
[ 84.0626, 1.6844, 1676.4392, 1118.7032, -864.5373, 189.7945, 1162.9518]], grad_fn=<DivBackward0>)
注意力得分矩阵维度是 n × n n \times n n×n,其中 n n n 是序列的长度。每个元素 ( i , j ) (i, j) (i,j) 表示第 i i i 个元素与第 j j j 个元素之间的相似度。
参考示意图如下:
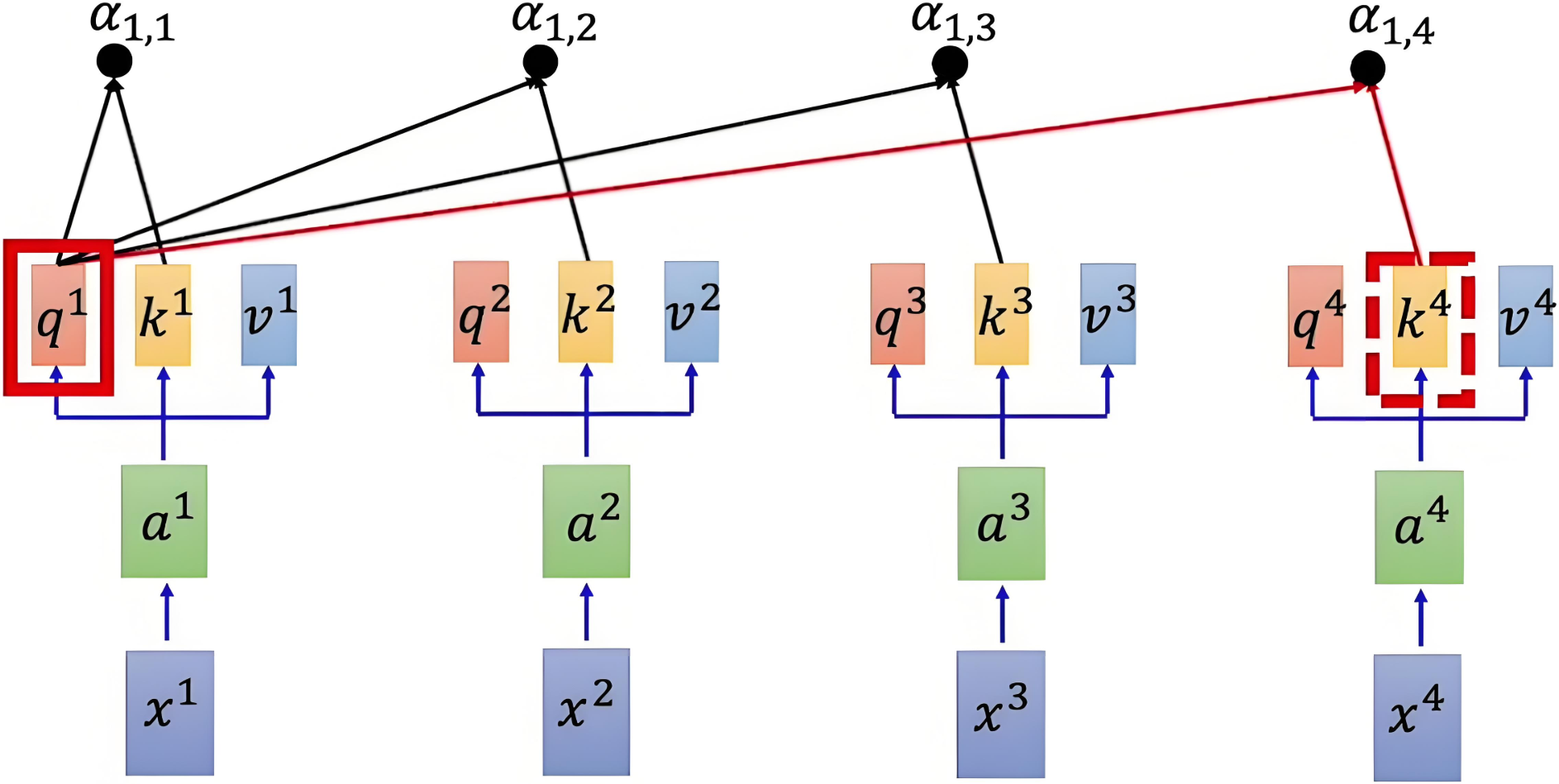 |
|---|
| α 1 , i = q 1 ⋅ k i d k \alpha_{1,i} = \frac{q^1 \cdot k^i}{\sqrt{d_k}} α1,i=dkq1⋅ki |
2.5 归一化
为了将注意力得分转换为概率分布,需按行对得分矩阵进行
s
o
f
t
m
a
x
softmax
softmax 操作,确保每行的和为 1,得到的矩阵表示每个元素对其他元素的注意力权重。是的,包括自己。
Attention Weight
=
softmax
(
Q
K
T
d
k
)
\text{Attention Weight} = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right)
Attention Weight=softmax(dkQKT)
具体到每行的公式如下:
α
^
1
,
i
=
exp
(
α
1
,
i
)
∑
j
exp
(
α
1
,
j
)
\hat{\alpha}_{1,i} = \frac{\exp(\alpha_{1,i})}{\sum_j \exp(\alpha_{1,j})}
α^1,i=∑jexp(α1,j)exp(α1,i)
- α 1 , i \alpha_{1,i} α1,i :第 1 1 1 个词语和第 i i i 个词语之间的原始注意力得分。
- α ^ 1 , i \hat{\alpha}_{1,i} α^1,i :经过归一化后的注意力得分。
参考代码如下:
# 注意力得分归一化
normalized_scores = F.softmax(scores, dim=1)
print(normalized_scores)
注:一行上进行归一化
2.6 加权求和
通过将注意力权重矩阵与值矩阵
V
V
V 相乘,得到加权的值表示。
Output
=
Attention Weight
×
V
=
softmax
(
Q
K
T
d
k
)
×
V
\text{Output} =\text{Attention Weight} \times V = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) \times V
Output=Attention Weight×V=softmax(dkQKT)×V
具体计算示意图如下:
 |
|---|
| Q和K计算相似度后,经 s o f t m a x softmax softmax 得到注意力,再乘V,最后相加得到包含注意力的输出 |
参考代码如下:
# 加权求和获取注意力后的结果
attention_result = torch.matmul(normalized_scores, Value)
print(attention_result.shape) # torch.Size([7, 512])
注:通过上下文来描述每一个词
2.7 输出
最终得到的输出是一个维度为 n × d v n \times d_v n×dv 的新矩阵,其中每个元素的表示都被加权了。
本质:将Query和Key分别计算相似性,然后经过softmax得到相似性概率权重即注意力,再乘以Value,最后相加即可得到包含注意力的输出
至此,艺术已成,我就是我,我不再是我。
3. 多头注意力机制
Multi-Head Attention,多头注意力机制,是对自注意力机制的扩展。
3.1 基本概念
多头注意力机制的核心思想是,将注意力机制中的 Q 、 K 、 V Q、K、V Q、K、V 分成多个头,每个头计算出独立的注意力结果,然后将所有头的输出拼接起来,最后通过一个线性变换得到最终的输出。
 |
|---|
| q i = W q a i q i , 1 = W q , 1 q i q i , 2 = W q , 2 q i q^{i}=W^{q}a^{i} \quad \quad q^{i,1}=W^{q,1}q^{i}\quad\quad q^{i,2}=W^{q,2}q^{i} qi=Wqaiqi,1=Wq,1qiqi,2=Wq,2qi |
注:多头注意力机制通常先将词向量映射为Q、K、V,然后再分成多个头。
# 随机生成自注意力机制的Query映射的权重矩阵
Wq = torch.randn(512, 512)
Query = torch.matmul(embedding_out, Wq)
# 随机生成自注意力机制的Key映射的权重矩阵
Wk = torch.randn(512, 512)
Key = torch.matmul(embedding_out, Wk)
# 随机生成自注意力机制的Value映射的权重矩阵
Wv = torch.randn(512, 512)
Value = torch.matmul(embedding_out, Wv)
3.2 多头机制
 |
|---|
| 2个头 |
3.2.1 映射权重
分头的过程是通过权重矩阵映射实现的,而不是直接切分,参考代码:
# 多头注意力层:分成4个头
head_num = 8 # 头的数量
d_k = dim // head_num # 每个头维度
# 随机生成多头注意力机制的Query映射的权重矩阵
W_Q_list = torch.stack([torch.randn(512, d_k) for _ in range(head_num)])
# 映射出每个头的Query
Query_list = torch.stack(
[torch.matmul(embedding_out, W_Q_list[i]) for i in range(head_num)]
)
print(Query_list.shape)
# 随机生成多头注意力机制的Key映射的权重矩阵
W_K_list = torch.stack([torch.randn(512, d_k) for _ in range(head_num)])
Key_list = torch.stack(
[torch.matmul(embedding_out, W_K_list[i]) for i in range(head_num)]
)
# 随机生成多头注意力机制的Value映射的权重矩阵
W_V_list = torch.stack([torch.randn(512, d_k) for _ in range(head_num)])
Value_list = torch.stack(
[torch.matmul(embedding_out, W_V_list[i]) for i in range(head_num)]
)
3.3 加权求和
每个头是独立计算的,使用自己的一套参数,得到每个头的输出:
O
h
=
A
h
V
h
O_h = A_h V_h
Oh=AhVh
其中,
O
h
∈
R
n
×
d
v
O_h \in \mathbb{R}^{n \times d_v}
Oh∈Rn×dv 是第
h
h
h 个头的输出。
参考代码1:归一化的注意力得分
# 计算各自的注意力得分
scores_list = torch.stack(
[
torch.matmul(Query_list[i], Key_list[i].transpose(0, 1))
for i in range(head_num)
]
)
scores_list = torch.stack(
[scores_list[i] / math.sqrt(d_k) for i in range(head_num)]
)
# 进行归一化操作
scores_list = torch.stack(
[F.softmax(scores_list[i], dim=-1) for i in range(head_num)]
)
print(scores_list)
参考代码2:各自的头输出
# 计算每个头的注意力结果
Output_list = [torch.matmul(scores_list[i], Value_list[i]) for i in range(head_num)]
print(Output_list.shape)
3.4 输出拼接
将所有头的输出进行拼接:
O
concat
=
[
O
1
,
O
2
,
…
,
O
h
]
∈
R
n
×
h
⋅
d
v
O_{\text{concat}} = [O_1, O_2, \dots, O_h] \in \mathbb{R}^{n \times h \cdot d_v}
Oconcat=[O1,O2,…,Oh]∈Rn×h⋅dv
其中,
O
concat
O_{\text{concat}}
Oconcat 是所有头拼接的结果,维度是
n
×
(
h
⋅
d
v
)
n \times (h \cdot d_v)
n×(h⋅dv),其中
h
h
h 是头的数量,
d
v
d_v
dv 是每个头的值向量的维度。
参考代码:
# 对8个头进行拼接,拼接形状:(seq_len, d_k)
Output = torch.cat(Output_list, dim=-1)
print(Output.shape) # torch.Size([7, 512])
3.5 线性变换
拼接后通过一个线性变换矩阵
W
O
W^O
WO 映射为最终输出:
Output
=
O
concat
W
O
\text{Output} = O_{\text{concat}} W^O
Output=OconcatWO
其中,
W
O
∈
R
(
h
⋅
d
v
)
×
d
W^O \in \mathbb{R}^{(h \cdot d_v) \times d}
WO∈R(h⋅dv)×d 是可训练的权重矩阵,
d
d
d 是最终输出的维度。
参考代码:
# 线性变换并最终输出
W_O = torch.randn(dim, dim)
Output = torch.matmul(Output, W_O)
print(Output.shape) # torch.Size([7, 512])
3.6 表达能力
通过多个并行的头在不同的子空间中学习上下文信息,让同一个句子在不同场景下表达不同的意思,增强模型的表达能力和灵活性。