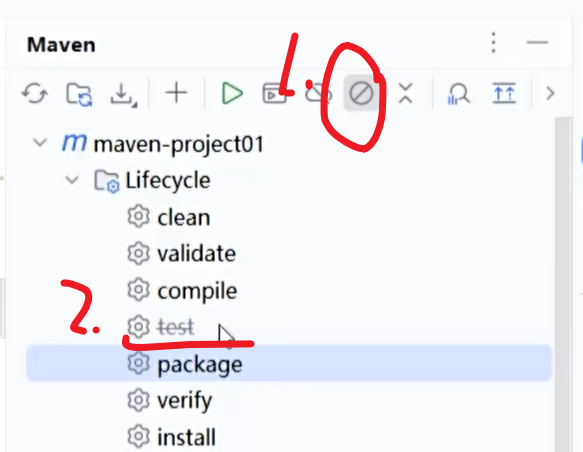
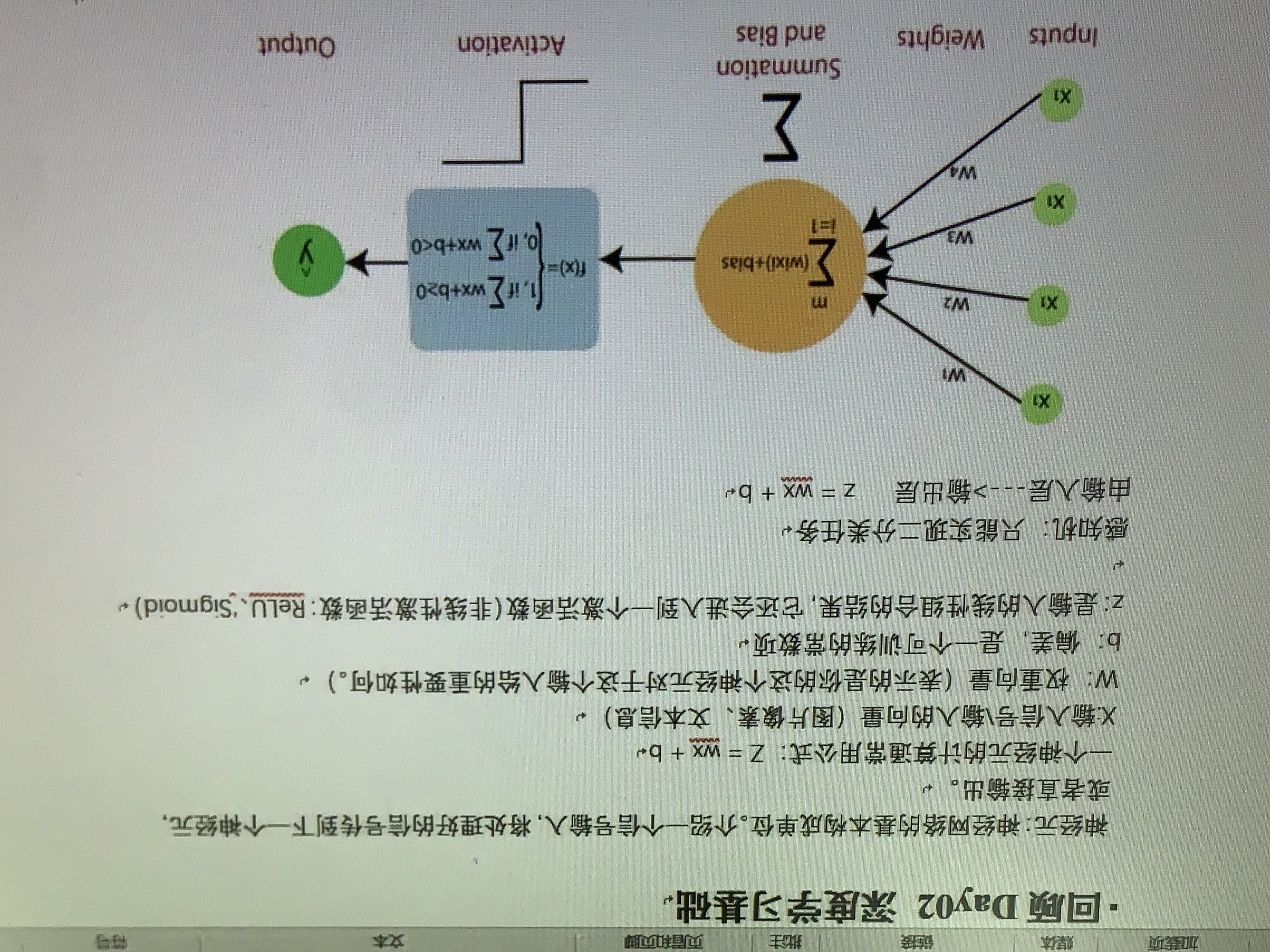
一、引言
上一节,我们介绍了希尔伯特黄变换(HHT)及其经验模态分解(EMD)的相关内容,这一节,我们继续拓展EMD分解技术,补充介绍集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)和变分模态分解(Variational Mode Decomposition,VMD)分解方法。
二、3种信号分解方法
2.1 经验模态分解(Empirical Mode Decomposition,EMD)
经验模态分解(Empirical Mode Decomposition,EMD),它能够将复杂的非平稳信号分解为若干个本征模态函数(Intrinsic Mode Functions,IMFs)。IMFs反映了信号在不同时间尺度上的局部特征。EMD分解过程是基于信号的局部极值点,通过不断筛选出信号中的局部极值点来构造上下包络线,从而得到各个IMFs。这一过程是自适应的,不需要预先设定信号的模型,能够很好地适应心电信号的非平稳特性。

图1 经验模态分解示意图
2.1.1. IMF的定义
一个本征模态函数(IMF)必须满足以下两个条件:
-
在整个数据段内,极值点(极大值点和极小值点)的数量和过零点的数量必须相等,或者最多相差一个。
-
在任意时刻,由局部极大值点定义的上包络和由局部极小值点定义的下包络的平均值为零。
2.1.2 EMD分解步骤
EMD分解过程可以分为以下几个步骤:
(1)寻找局部极值点
-
对于给定的信号 s(t),首先找到所有的局部极大值点和极小值点。局部极大值点是指在该点及其邻域内,信号值达到局部最大值;局部极小值点是指在该点及其邻域内,信号值达到局部最小值。
(2)构造上下包络线
- 使用三次样条插值方法,通过局部极大值点构造上包络线 Eupper(t),通过局部极小值点构造下包络线 Elower(t)。包络线的构造公式如下:


(3)计算均值
-
计算上下包络线的均值 m(t):

(4)筛选过程
-
从原始信号中减去均值 m(t),得到新的信号 h(t):
![]()
-
检查 h(t) 是否满足IMF的条件。如果满足,则 h(t) 是一个IMF;如果不满足,则将 h(t) 作为新的信号,重复上述步骤,直到满足IMF的条件。
(5)分解IMFs
-
重复上述过程,从原始信号中逐步提取出各个IMF。每次提取一个IMF后,从原始信号中减去该IMF,得到剩余信号,然后对剩余信号继续进行EMD分解,直到剩余信号不再包含任何IMF为止。
2.1.3 EMD分解的数学表示
假设原始信号为 s(t),通过EMD分解可以得到 n 个IMF和一个残差 r(t):
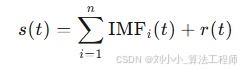
其中,IMFi(t) 表示第 i 个本征模态函数,r(t) 是分解后的残差,包含信号的低频趋势或噪声成分。
2.2 集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)
2.2.1 EEMD分解步骤
EEMD 是 EMD 的改进方法,通过在原始信号中添加白噪声来解决模态混叠问题。其步骤如下:
-
向原始信号 x(t) 添加白噪声:xnoisy(t)=x(t)+noise(t)。
-
对加噪信号 xnoisy(t) 进行 EMD 分解,得到一组 IMF 分量 {ci,j(t)},其中 i 表示第 i 个 IMF 分量,j 表示第 j 次加噪。
-
重复上述过程 N 次。
-
对 N 次分解得到的 IMF 分量进行集合平均,得到最终的 IMF 分量:

2.2.2 EEMD的数学表述
EEMD 分解可以表示为:
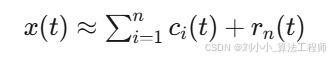
其中,ci(t) 是通过集合平均得到的第 i 个 IMF 分量,rn(t) 是最终残差。
2.3 变分模态分解(Variational Mode Decomposition,VMD)
2.3.1 目标函数构建
变分模态分解(VMD)是一种基于变分优化框架的自适应信号分解方法,旨在将复杂信号分解为多个具有稀疏频带特性的本征模态函数(Band-Limited Intrinsic Mode Functions, BLIMFs)。其核心思想是通过数学优化手段,在频域内自适应地划分信号频谱,从而克服传统经验模态分解(EMD)的模态混叠和端点效应问题。
VMD的核心是构造一个约束优化问题,要求每个模态函数 uk(t) 的带宽最小化,同时保证所有模态的线性组合等于原始信号 f(t) 。其数学模型为:

物理意义:
-
∂t表示时间导数:约束每个模态的瞬时变化特性。
-
Hilbert变换项 (δ(t)+jπt)∗uk(t):将模态转换为解析信号,便于频域分析。
-
指数项 e^−jωkt:将模态的频谱搬移到基带,简化带宽计算。
-
目标函数最小化:迫使每个模态 uk(t)的能量集中在以 ωk 为中心的窄带内。
2.3.2 约束条件的松弛化
为便于求解,引入拉格朗日乘子 λ(t) 和二次惩罚项,将原约束优化问题转化为无约束形式:

其中:
-
α:带宽约束因子,控制模态的带宽(α 越大,模态带宽越窄)。
-
二次惩罚项:增强算法对噪声的鲁棒性。
2.3.3 交替方向乘子法(ADMM)求解
通过交替方向乘子法(ADMM)迭代更新模态 uk、中心频率 ωk,以及拉格朗日乘子 λλ。
(1) 模态更新(频域形式)
在频域中,模态函数的更新方程为:

-
将时域信号转换至频域,简化微分运算。
-
通过引入拉格朗日乘子的频域形式 λ^(ω) ,分离各模态的耦合。
-
分母项 1+2α(ω−ωk)^2 体现带宽约束,迫使能量集中在 ωk 附近。
(2) 中心频率更新
中心频率 ωk 通过能量重心法更新:

新的中心频率是模态功率谱的加权平均,确保每个模态的频谱能量集中在其中心频率附近。
(3) 拉格朗日乘子更新
拉格朗日乘子用于强制约束条件的满足:

其中 τ (tao)为更新步长(噪声容忍参数),控制收敛速度。
(4)模态数 K
-
选择依据:根据信号的频谱特征预先设定。若 K 过小,导致模态欠分解;若 K 过大,引入虚假模态。
-
心电信号建议:通常取 K=6∼10,覆盖QRS波(高频)、P/T波(中频)、基线漂移(低频)。
三、EEMD和VMD在心电信号特征提取中的应用
3.1 实验过程
通过对心电信号进行EMD/EEMD/VMD分解,我们得到了多个IMF。每个IMF代表了心电信号的一个局部特征,可以用于进一步的分析和诊断。以下是具体的实验结果和分析:
-
图2展示了原始心电信号的波形,可以看出心电信号的周期性和波动性。

图2 原始心电信号(mitdb-222号记录)
3.1.1 EMD分解结果
-
图3展示了EMD分解后的9个IMF。每个IMF代表了心电信号的一个局部特征,可以用于进一步的分析和诊断。

图3 EMD分解(mitdb-222号记录)
-
图4展示了EMD分解结果的小窗显示,通过偏移量区分不同的IMF,便于观察和比较。

图4 EMD分解的偏移量小窗显示(mitdb-222号记录)
(3)IMF的瞬时频率
-
图5展示了IMF2的瞬时频率。瞬时频率的变化可以反映心电信号的动态特性,有助于识别心电信号中的异常特征。

图5 EMD-IMF2的瞬时频率(mitdb-222号记录)
3.1.2 EEMD分解结果
选择噪声系数为0.2,迭代次数为100,进行EEMD分解,结果如下所示。

图6 EEMD分解(mitdb-222号记录)

图7 EEMD分解的偏移量小窗显示(mitdb-222号记录)

图8 EEMD-IMF2的瞬时频率(mitdb-222号记录)
3.1.3 VMD分解结果
选择如下参数,对原始心电信号进行VMD分解,结果如下所示。
%--------- 对于VMD参数进行设置---------------
alpha = 2000; % moderate bandwidth constraint:适度的带宽约束/惩罚因子
tau = 0.0244; % noise-tolerance (no strict fidelity enforcement):噪声容限(没有严格的保真度执行)
K = 10; % modes:分解的模态数
DC = 0; % no DC part imposed:无直流部分
init = 1; % initialize omegas uniformly :omegas的均匀初始化

图9 VMD分解(mitdb-222号记录)

图10 VMD分解的偏移量小窗显示(mitdb-222号记录)

图11 VMD-IMF2的瞬时频率(mitdb-222号记录)
四、实验结果与分析
(一)EEMD/VMD 在心电信号特征提取中的优势
-
EEMD 的优势 (1)通过添加白噪声,解决了传统 EMD 中的模态混叠问题,提高了分解结果的稳定性和可靠性。 (2)能够自适应地分解心电信号中的多频率成分,提取出不同频率段的特征信息,有助于更准确地分析心电信号的时频特性。
-
VMD 的优势 (1)在分解过程中能够自适应地确定模态函数的中心频率和带宽,避免了传统 EMD 方法中存在的端点效应问题。 (2)通过优化模型实现信号分解,分解结果更加合理且具有物理意义,能够更好地反映心电信号的内在结构。
(二)EEMD 和 VMD 分解结果比较
-
分解效果: EEMD 和 VMD 都能有效地将心电信号分解为多个分量。EEMD 的分解结果受白噪声影响,具有一定的随机性;VMD 的分解结果更稳定,且无模态混叠。
-
计算效率: VMD 可并行实现,计算效率高于 EEMD。
-
适用场景: 对于需要精确特征提取的场景,VMD 更适用;对于对随机性有一定容忍度的场景,EEMD 也能取得较好的效果。
通过实验验证了 EEMD 和 VMD 在心电信号特征提取中的有效性。实验数据为从 222.dat 文件中读取的心电信号,采样频率为 360 Hz。分别采用 EEMD 和 VMD 方法对心电信号进行分解,得到多个 IMF 分量,并绘制了分解结果的大窗图和小窗图。从分解结果可以看出,两种方法都能够有效地将心电信号分解为多个具有不同频率特性的 IMF 分量。进一步对 IMF 分量进行功率谱密度分析和瞬时频率计算,提取了心电信号的特征信息,为心律失常检测等应用提供了基础。
Tips:下一讲,我们将进一步探讨,心电信号特征提取——傅里叶变换谱、小波谱与希尔伯特谱分析等。
以上就是EMD/EEMD/VMD 信号分解方法的全部内容啦~
我们下期再见,拜拜(⭐v⭐) ~
(Ps:有代码实现需求,请见主页信息,谢谢支持!~)