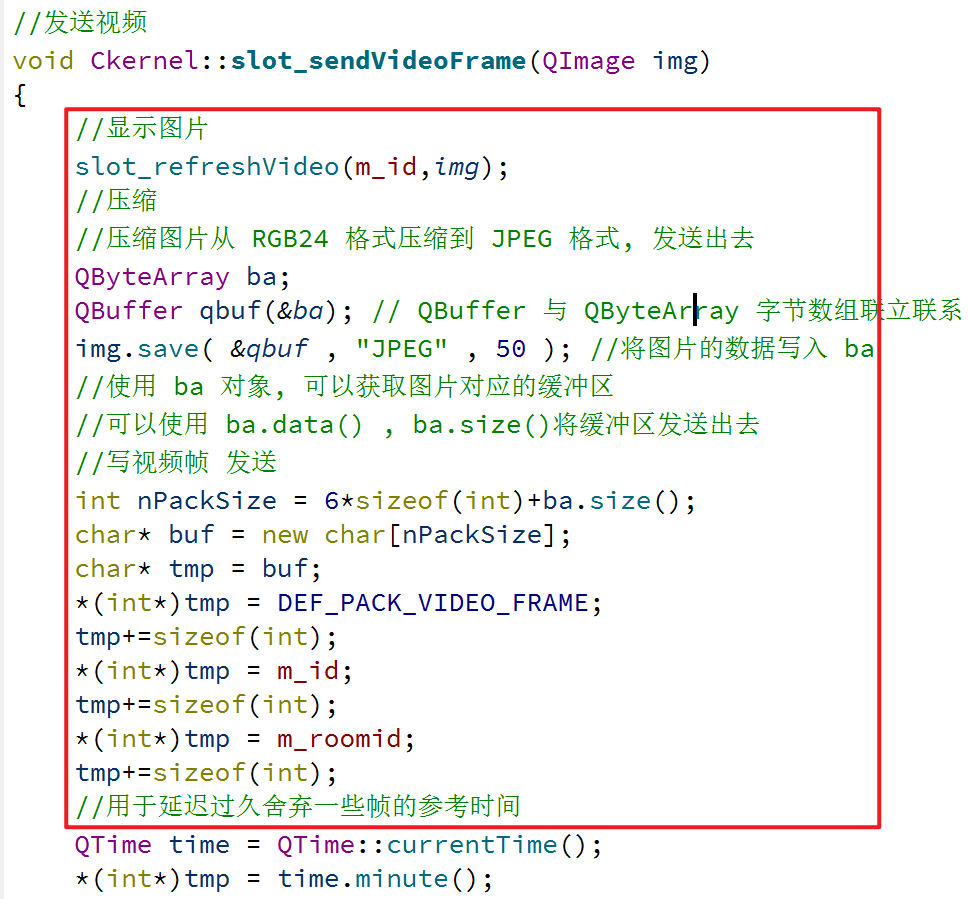
文章目录
- 分割中的上/下采样
- 下采样
- SegFormer和PVT(使用卷积)
- Swin-Unet(使用 Patch Merging)
- 上采样
- SegFormer(interpolate)
- Swin-Unet(Patch Expanding)
- 逐级interpolate的方式
- 反卷的方式
在基于Transformer架构的图像分割模型(如 SegFormer、Swin-Unet)中,上采样和下采样结构几乎是标准配置。
分割中的上/下采样
为什么需要下采样?
-
提取高层语义特征:
Transformer擅长全局建模,结合下采样可以:降低分辨率;聚焦于更宽范围的上下文。 -
减少计算成本:
原始输入图像太大,直接送入多层Transformer(特别是多头注意力)会导致计算量和显存爆炸。
为什么要上采样?
-
恢复空间分辨率:
Segmentation任务最终要输出与输入图像同样大小的分割mask; -
细粒度定位:
但如果没有上采样、跳跃连接或融合,容易失去细节;所以上采样常结合UNet-like结构来补偿细节损失。
| 模型 | 下采样方式 | 上采样方式 |
|---|---|---|
| SETR | ViT backbone patchify | 多层反卷积上采样 |
| SegFormer | MLP Mixer + 4阶段卷积下采样 | 多层插值 + FFN |
| Swin-Unet | Swin Transformer 下采样 | Patch expanding + skip连接 |
下采样
SegFormer和PVT(使用卷积)
# 输入:img.shape = [B, 3, 512, 512]
# Stage 1
x1 = Conv2d(3, 32, kernel_size=7, stride=4, padding=3)(img) # → [B, 32, 128, 128]
x1 = x1.flatten(2).transpose(1, 2) # → [B, 16384, 32]
x1 = TransformerBlock(x1)
# Stage 2
x2 = Conv2d(32, 64, kernel_size=3, stride=2, padding=1)(x1_reshaped) # → [B, 64, 64, 64]
x2 = x2.flatten(2).transpose(1, 2) # → [B, 4096, 64]
x2 = TransformerBlock(x2)
# 后面还有 Stage3、Stage4 类似
Shape 演化:
Stage1: [B, 128×128=16384, 32]
Stage2: [B, 64×64=4096, 64]
Stage3: [B, 32×32=1024, 160]
Stage4: [B, 16×16=256, 256]
Swin-Unet(使用 Patch Merging)
# 初始 patch embedding(patch_size=4)
x = Conv2d(3, 96, kernel_size=4, stride=4)(img) # [B, 96, 128, 128]
x = x.flatten(2).transpose(1, 2) # → [B, 16384, 96]
# Stage 1
x = SwinBlock(x) # [B, 16384, 96]
x = PatchMerging(x) # → [B, 4096, 192]
# Stage 2
x = SwinBlock(x) # [B, 4096, 192]
x = PatchMerging(x) # → [B, 1024, 384]
# Stage 3
x = SwinBlock(x)
x = PatchMerging(x) # → [B, 256, 768]
Shape 演化:
Stage0: [B, 128×128=16384, 96]
Stage1: [B, 64×64=4096, 192]
Stage2: [B, 32×32=1024, 384]
Stage3: [B, 16×16=256, 768]
过程不难,只是不好描述,可以看相关教程,这里就把代码贴出来
class PatchMerging(nn.Module):
def __init__(self, in_dim):
super().__init__()
self.reduction = nn.Linear(in_dim * 4, in_dim * 2)
def forward(self, x, H, W):
# x: [B, H*W, C] → [B, H, W, C]
x = x.view(B, H, W, C)
# 拆分四个方向的 token
x0 = x[:, 0::2, 0::2, :] # top-left
x1 = x[:, 1::2, 0::2, :] # bottom-left
x2 = x[:, 0::2, 1::2, :] # top-right
x3 = x[:, 1::2, 1::2, :] # bottom-right
x = torch.cat([x0, x1, x2, x3], dim=-1) # → [B, H/2, W/2, 4C]
x = x.view(B, -1, 4 * C) # → [B, H/2*W/2, 4C]
x = self.reduction(x) # → [B, H/2*W/2, 2C]
return x
上采样
SegFormer(interpolate)

def forward(self, x1, x2, x3, x4):
# 输入来自4个Stage:
# x1: [B, 128*128, 32]
# x2: [B, 64*64, 64]
# x3: [B, 32*32, 160]
# x4: [B, 16*16, 256]
B = x1.shape[0]
# === 1. Linear Projection:通道都投影为 256 ===
_x1 = self.linear1(x1).permute(0, 2, 1).reshape(B, 256, 128, 128) # [B, 256, 128, 128]
_x2 = self.linear2(x2).permute(0, 2, 1).reshape(B, 256, 64, 64) # [B, 256, 64, 64]
_x3 = self.linear3(x3).permute(0, 2, 1).reshape(B, 256, 32, 32) # [B, 256, 32, 32]
_x4 = self.linear4(x4).permute(0, 2, 1).reshape(B, 256, 16, 16) # [B, 256, 16, 16]
# === 2. 上采样到统一大小 ===
_x2 = F.interpolate(_x2, size=(128, 128), mode='bilinear', align_corners=False) # [B, 256, 128, 128]
_x3 = F.interpolate(_x3, size=(128, 128), mode='bilinear', align_corners=False) # [B, 256, 128, 128]
_x4 = F.interpolate(_x4, size=(128, 128), mode='bilinear', align_corners=False) # [B, 256, 128, 128]
# === 3. 拼接所有层 ===
fused = torch.cat([_x1, _x2, _x3, _x4], dim=1) # [B, 4*256=1024, 128, 128]
# === 4. 1x1卷积融合通道数 ===
out = self.fuse_conv(fused) # [B, 256, 128, 128]
return out
Swin-Unet(Patch Expanding)
看图也能看出来,十分经典的U-Net结构。

在上采样阶段
输入:
一个高语义 token,维度为 [4C],是上一步 Patch Merging 得到的。
-
Linear 映射
将[4C]投影为[C] × 4,也就是还原为 2×2 patch 每格的C维向量。 -
reshape → [H, W, 2, 2, C] → [2H, 2W, C]
把这 4 个 token 安排到一个新的空间位置(上采样 ×2)。 -
最终输出为:
Token 数量 × 4 , 通道数 ÷ 2 \text{Token 数量} \times 4,\quad \text{通道数} \div 2 Token 数量×4,通道数÷2
class PatchExpanding(nn.Module):
def __init__(self, in_dim, expand_ratio=2):
super().__init__()
# Linear: [B, H*W, in_dim] → [B, H*W, out_dim = (expand_ratio^2) * out_channels]
# 例如:in_dim = 512,expand_ratio = 2 → 输出 4×C = 1024
self.linear = nn.Linear(in_dim, in_dim // 2 * expand_ratio**2)
self.expand_ratio = expand_ratio
def forward(self, x, H, W):
# x: [B, H*W, C]
B, N, C = x.shape
R = self.expand_ratio # 通常为 2
# 线性投影:C → 4 * (C/2),也就是 [B, H*W, 4*C'],每个 token 展开为 2×2 的 patch
x = self.linear(x) # [B, H*W, 4*C'] = [B, H*W, R*R*(C//2)]
# reshape 成图像形式,带有 2×2 子结构 → [B, H, W, R, R, C']
x = x.view(B, H, W, R, R, C // 2) # [B, H, W, 2, 2, C//2]
# 调整顺序,将 2×2 子结构移入空间维度 → [B, H*2, W*2, C//2]
x = x.permute(0, 1, 3, 2, 4, 5) # [B, H, 2, W, 2, C//2]
x = x.reshape(B, H * R, W * R, C // 2) # [B, 2H, 2W, C//2]
# flatten 成 token 序列形式(可再送入 Transformer)→ [B, 4*H*W, C//2]
x = x.view(B, -1, C // 2) # [B, 4*H*W, C//2]
return x
逐级interpolate的方式
-
输入来自编码器 4 个 stage:
x4:[16×16, 512] ← 最深层x3:[32×32, 320]x2:[64×64, 128]x1:[128×128, 64] ← 最浅层
-
通道统一:
每个特征图先通过 1×1 卷积或 Linear 映射,统一成相同维度(如全部 → 256 或 512) -
上采样与融合(逐级):
f4 = Conv(x4) # [16×16] f3 = F.interpolate(f4, scale=2) + Conv(x3) # → [32×32] f2 = F.interpolate(f3, scale=2) + Conv(x2) # → [64×64] f1 = F.interpolate(f2, scale=2) + Conv(x1) # → [128×128]
反卷的方式
很经典的设计,不必过多介绍。