【数据结构】_二叉树

news2025/5/18 9:43:58

在这里插入图片描述

1.二叉树链式结构的实现

1.1 前置说明

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->_left = node2;
	node1->_right = node4;
	node2->_left = node3;
	node4->_left = node5;
	node4->_right = node6;
	return node1;
}

❗❗❗注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：
1.空树
2.非空：根节点，根节点的左子树、根节点的右子树组成的。

从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

2.二叉树的遍历

2.1 前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

  1. 前序遍历——访问根结点的操作发生在遍历其左右子树之前。（根 左子树 右子树）
  2. 中序遍历——访问根结点的操作发生在遍历其左右子树之中。（左 根 右）
  3. 后序遍历——访问根结点的操作发生在遍历其左右子树之后。（左 右 根）

任何一个二叉树，都要看做三个部分

根节点、左子树、右子树

🤗🤗🤗下面我们来看看这三种的遍历顺序叭

  1. 前序遍历
    在这里插入图片描述

  2. 中序遍历在这里插入图片描述

  3. 后序遍历在这里插入图片描述

  4. 层序遍历在这里插入图片描述

判断一个树是不是完全二叉树可以用层序遍历
因为假设D没有，那么就会是ABC null E…这样会有一个null隔开来

2.2前序遍历实现

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>


typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;

}BTNode;
	


//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->_data);//打印根
	PrevOrder(root->_left);
	PrevOrder(root->_right);
}



//求二叉树的结点个数	
int TreeSize(BTNode* root)//传的是根结点的指针
{
	return 0;
}


//创建树
BTNode* GreateNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}


int main()
{
	BTNode* A = GreateNode('A');
	BTNode* B = GreateNode('B');
	BTNode* C = GreateNode('C');
	BTNode* D = GreateNode('D');
	BTNode* E = GreateNode('E');

	A->_left = B;
	A->_right = C;
	B->_left = D;
	B->_right = E;

	PrevOrder(A);
	return 0;
}

运行结果：

在这里插入图片描述

前序遍历递归展开过程：

在这里插入图片描述

2.3中序遍历的实现

由前序遍历我们可以知道交换根左右那个递归代码的顺序就能退出中、后续遍历，只用改变这一个递归的顺序

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->_left);
	printf("%c ", root->_data);//打印根
	InOrder(root->_right);
}

2.4后序遍历的实现

//后续遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%c ", root->_data);//打印根
}

2.5求二叉树的结点个数

在很多时候，我们会直接这样写，但是我们会发现最后的结果是错误的，原因就是每一个递归里面都有一个size，这个size始终都加不到一个size上面，就只能加一次，这个size是局部变量，我们就要思考一下如何加到同一个size上面呢？？

错误写法：

//求二叉树的结点个数	
int TreeSize(BTNode* root)//传的是根结点的指针
{
	if (root == NULL)
	{
		return 0;
	}
	int size = 0;
	size++;
	TreeSize(root->_left);
	TreeSize(root->_right);

	return size;
}

运行结果：TreeSize=1（是错误的）

方法一：

修改成全局变量

//求二叉树的结点个数	
int size = 0;
int TreeSize(BTNode* root)//传的是根结点的指针
{
	if (root == NULL)
	{
		return 0;
	}
	
	size++;
	TreeSize(root->_left);
	TreeSize(root->_right);

	return size;
}

//int main函数里面
printf("TreeSize:%d\n", TreeSize(A));
printf("TreeSize:%d\n", TreeSize(A));

但这里存在一个缺陷，就是再次调用时会相互影响

在这里插入图片描述

方法二：


//求二叉树的结点个数	
void TreeSize(BTNode* root,int* psize)//传的是根结点的指针
{
	if (root == NULL)
	{
		return;
	}
	else
	{
		(*psize)++;
	}

	TreeSize(root->_left, psize);
	TreeSize(root->_right, psize);

}

//int main函数里面
int sizea = 0;
TreeSize(A, &sizea);
printf("TreeSize:%d\n", sizea);


int sizeb = 0;
TreeSize(B, &sizeb);
printf("TreeSize:%d\n", sizeb);

在这里插入图片描述

方法三：

//求二叉树的结点个数	
int TreeSize(BTNode* root)
{
	//空树
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		return 1 + TreeSize(root->_left) + TreeSize(root->_right);
	}
}

在这里插入图片描述

这里就不会相互影响

2.6求叶子结点个数

//求叶子结点个数
int TreeLeafSize(BTNode* root)
{
	//空树
	if (root == NULL)
	{
		return 0;//如果传入的节点指针为NULL，表示这是一个空树或空子树
                 //空树没有叶子节点，所以返回0
	}
	if (root->_left == NULL && root->_right == NULL)
	{
	             //如果一个节点的左右子节点都为NULL，那么这个节点就是叶子节点
		return 1;//每找到一个叶子节点就返回1
	}

	return TreeSize(root->_left) + TreeSize(root->_right);
	//对于非叶子节点，递归计算其左子树和右子树的叶子节点数量
	//将左右子树的叶子节点数量相加，得到当前子树的叶子节点总数
}

运行结果：

在这里插入图片描述

2.7二叉树第k层节点个数

当前树的第k层节点数，等于其左子树的第k-1层节点数加上右子树的第k-1层节点数。
层数=1时就不需要再分解

这句话的意思就是：
从根节点 A（k=3）的视角看
A 的第3层节点，其实是A的左子树（根为 B）的第2层节点和右子树（根为 C）的第2层节点之和。
为什么？因为：
左子树（B 为根）的第1层是B自己（对应原树的第 2 层），第2层是B的子节点（D、E，对应原树的第3层）。
右子树（C 为根）的第1层是C自己（对应原树的第 2 层），第2层是C的子节点 F（对应原树的第3层）。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;//如果当前节点为空，说明该路径上没有节点，返回 0
	}
	if (k == 1)
	{
		return 1;//当层数 k 递减到 1 时，表示当前节点就是目标层的节点，返回 1
	}
	return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

main函数中调用：

在这里插入图片描述

画图解释：
在这里插入图片描述

运行结果：

在这里插入图片描述

2.8二叉树查找值为x的节点

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;//如果当前节点为空，返回 NULL
	}
	if (root->_data == x)
	{
		return root;//如果当前节点的值等于 x，返回当前节点
	}
	//这里我们用的前序遍历
	//没找到 我们就找左
	BTNode* node = BinaryTreeFind(root->_left, x);
	if (node)
	{
		return node;//否则递归查找左子树，若找到则返回该节点
	}

	node = BinaryTreeFind(root->_right, x);
	if (node)
	{
		return node;//若左子树未找到，递归查找右子树，找到则返回
	}
	return NULL;//若左右子树均未找到，返回 NULL
}

2.9销毁二叉树

//销毁树
void DestoryTree(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//用后续销毁
	DestoryTree(root->_left);
	DestoryTree(root->_right);
	free(root);
}

2.10二叉树的层序遍历

画图解释层序遍历的原理：
在这里插入图片描述
层序遍历的实现原理：

层序遍历的目标是从上到下、从左到右依次访问二叉树的每个节点。实现这一目标的关键在于利用队列的先进先出特性：

  • 根节点入队：首先将根节点放入队列。
  • 循环处理队列：只要队列不为空，就执行以下操作：
  • 出队当前节点：取出队列头部的节点并访问（打印数据）。
  • 子节点入队：将当前节点的左子节点和右子节点（如果存在）依次加入队列。
  • 重复步骤 2：由于队列的先进先出特性，下层的节点会在当前层的所有节点处理完毕后才被处理，从而保证了层序遍历的顺序。

其在Queue.h文件中需要声明：

//声明一下
struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;

代码分析：

//二叉树的层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);// 初始化队列
	if (root == NULL)// 处理空树的情况
	{
		return;
	}
	QueuePush(&q, root);// 将根节点入队

	while (!QueueEmpty(&q)) // 当队列不为空时循环
	{
		BTNode* front = QueueFront(&q); // 获取队头节点
		QueuePop(&q); // 队头节点出队
		printf("%c ", front->_data); // 访问当前节点（打印数据）

		if (front->_left)// 如果左子节点存在，将其入队
		{
			QueuePush(&q, front->_left);
		}

		if (front->_right)// 如果右子节点存在，将其入队
		{
			QueuePush(&q, front->_right);
		}
	}
	QueueDestory(&q); // 销毁队列，释放资源
	printf("\n");
}

关键步骤解析

  • 队列初始化与根节点入队：
    • 创建队列并初始化，若根节点不为空则将其入队。这是遍历的起点。
  • 循环处理队列：
    • 出队并访问当前节点：每次从队列头部取出节点并打印其数据。
    • 子节点入队：按左、右顺序将子节点加入队列。由于队列的 FIFO 特性，这些子节点会在当前层的所有节点处理完毕后才被处理。
  • 队列管理：
    • 空队列检测：循环条件!QueueEmpty(&q)确保所有节点都被处理后终止循环。
    • 资源释放：遍历结束后销毁队列，避免内存泄漏。

运行结果：
在这里插入图片描述

2.11判断二叉树是否是完全二叉树

本题运用的是层序遍历
是完全二叉树返回1 ，不是返回0

在这里插入图片描述

// 判断二叉树是否是完全二叉树
//是返回1 不是返回0
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);// 初始化队列
	if (root == NULL)// 处理空树的情况
	{
		return 1;// 空树被视为完全二叉树
	}

	QueuePush(&q, root);// 将根节点入队

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); // 获取队头节点
		QueuePop(&q); // 队头节点出队
		//只要出来为空 咱就break
		// 只要出队节点为空，立即终止循环
		if (front == NULL)
		{
			break;
		}
		//把左右录进去（无论是否为空）
		QueuePush(&q, front->_left);
		QueuePush(&q, front->_right);
	}
	
	//下面只要有一个非空就不是完全二叉树
	// 检查队列中剩余的节点
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); // 获取队头节点
		QueuePop(&q); // 队头节点出队
		 // 若发现非空节点，则不是完全二叉树
		if (front)
		{
			QueueDestory(&q);//防止内存泄露
			return 0;
		}
	}
	QueueDestory(&q);
	return 1;
}

关键点解析：

  • 队列的使用：通过队列实现层序遍历，确保节点按层级顺序处理。
  • 首次遇到空节点：当层序遍历中首次遇到空节点时，立即终止第一层循环。
  • 剩余节点检查：检查队列中剩余的所有节点。若存在非空节点，则二叉树不是完全二叉树。
  • 内存管理：在返回结果前销毁队列，避免内存泄漏。

运行结果：

在这里插入图片描述

3.二叉树的相关OJ题

3.1二叉树的前序遍历

在这里插入图片描述

要求：Note: The returned array must be malloced, assume caller calls free().

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;

}BTNode;


int TreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + TreeSize(root->_left) + TreeSize(root->_right);
}


//辅助递归函数
void _preorderTraversal(BTNode* root, int* array, int* pi)//数组，数组里面第几个数
{
	if (root == NULL)
	{
		return;//如果当前节点为空，直接返回
	}
	//否则将当前节点的值存入数组array的当前位置*pi
	array[(*pi)++] = root->_data;
	//然后递归遍历左子树和右子树
	_preorderTraversal(root->_left, array, pi);
	_preorderTraversal(root->_right, array, pi);
	
	//注意：pi是一个指向整数的指针，用于跟踪当前存储位置，每次存入后会递增
}


//对外接口函数
int* preorderTraversal(BTNode* root, int* returnSize)
{
	//首先调用TreeSize计算树的节点数
	int size = TreeSize(root);
	//定义一个数组
	int* array = (int*)malloc(sizeof(int) * size);//动态分配足够的内存来存储遍历结果
	//下标
	int i = 0;//初始化索引i为 0
	_preorderTraversal(root, array, &i);//调用辅助函数进行实际的遍历

	*returnSize = size;//设置返回的大小，并返回存储结果的数组指针
	return array;
}


int main()
{
	// 构建二叉树节点
	BTNode* node1 = (BTNode*)malloc(sizeof(BTNode));
	node1->_data = 1;
	node1->_left = NULL;
	node1->_right = NULL;

	BTNode* node2 = (BTNode*)malloc(sizeof(BTNode));
	node2->_data = 2;
	node2->_left = NULL;
	node2->_right = NULL;

	BTNode* node3 = (BTNode*)malloc(sizeof(BTNode));
	node3->_data = 3;
	node3->_left = NULL;
	node3->_right = NULL;

	node1->_right = node2;
	node2->_right = node3;

	// 调用前序遍历函数
	int returnSize;
	int* result = preorderTraversal(node1, &returnSize);
	//以二叉树的根节点node1作为参数调用preorderTraversal函数
	//该函数会返回存储前序遍历结果的数组指针
	//同时通过&returnSize获取结果数组的大小 以便后续输出结果


	// 输出前序遍历结果
	printf("前序遍历结果: ");
	for (int i = 0; i < returnSize; i++)
	{
		printf("%d ", result[i]);//遍历存储前序遍历结果的数组result 按照顺序输出数组中的元素
	}
	printf("\n");

	// 释放动态分配的内存
	free(node1);
	free(node2);
	free(node3);
	free(result);

	return 0;
}

这道题目的意思其实就是，通过前序的方法把二叉树的有效值放到我们自己开辟的动态数组里面。
简单来说就是我们原先学了前序遍历，其有一个排序，将这个排好的顺序存储到数组里面，再通过数组遍历出来；就是先动态开辟一个数组 也就是preorderTraversal，然后再调用_preorderTraversal排序 ，相当于之前的前序遍历去遍历出来，再把它存到数组里面，最后再用*returnSize = size这个size在int main里面遍历出这个数组

结果：

在这里插入图片描述

3.2单值二叉树

在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;

}BTNode;


//创建树
BTNode* GreateNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}


bool isUnivalTree(BTNode* root)
{
	if (root == NULL)
	{
		return true;
	}
	
	//当前树
	if (root->_left && root->_data != root->_left->_data)
	{
		return false;
	}
	if (root->_right && root->_data != root->_right->_data)
	{
		return false;
	}

	//递归判断左右子树
	return isUnivalTree(root->_left) && isUnivalTree(root->_right);
}


int main()
{
	BTNode* A = GreateNode('1');
	BTNode* B = GreateNode('1');
	BTNode* C = GreateNode('1');
	BTNode* D = GreateNode('1');
	BTNode* E = GreateNode('1');
	BTNode* F = GreateNode('1');


	A->_left = B;
	A->_right = C;
	B->_left = D;
	B->_right = E;
	C->_right = F;

	
	if (isUnivalTree(A) == true)
	{
		printf("是单值二叉树：true");
	}
	else
	{
		printf("不是单值二叉树：false");
	}
}

核心代码的详细分析

bool isUnivalTree(BTNode* root)
{
	if (root == NULL)
	{
		return true;
	}
	
	//当前树
	if (root->_left && root->_data != root->_left->_data)
	{
		return false;
	}
	if (root->_right && root->_data != root->_right->_data)
	{
		return false;
	}

	//递归判断左右子树
	return isUnivalTree(root->_left) && isUnivalTree(root->_right);
}
  • 1.空树处理
    如果根节点为空（root == NULL），直接返回 true。
    这是因为空树被视为单值二叉树（没有节点，自然不存在值不同的节点）
  • 2.当前节点与子节点的比较
    • 检查左子节点：如果左子节点存在（root->_left != NULL），且其值不等于当前节点的值（root->_data != root->_left->_data），则返回false。
    • 检查右子节点：同理，如果右子节点存在且值不同，也返回 false。

关键点：只要当前节点的任一子节点值与当前节点不同，整棵树就不是单值二叉树，立即返回 false。

  • 递归检查左右子树
    • 递归检查左子树：调用isUnivalTree(root->_left)判断左子树是否为单值。
    • 递归检查右子树：调用isUnivalTree(root->_right)判断右子树是否为单值。
    • 返回结果：只有左右子树都为单值二叉树时，整棵树才是单值二叉树，因此用&&连接两个递归结果。

总结

这个函数通过递归的方式，从根节点开始逐层检查每个节点的值是否与子节点相同，确保整棵树所有节点的值一致。只要有任何一个节点的值与子节点不同，就会立即终止递归并返回 false。

3.3二叉树的最大深度

在这里插入图片描述

题意：该题求的是二叉树有多少层

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;

}BTNode;


//创建树
BTNode* GreateNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}

//二叉树的最大深度
int maxDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = maxDepth(root->_left);
	int rightDepth = maxDepth(root->_right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;

}

int main()
{
	BTNode* A = GreateNode('3');
	BTNode* B = GreateNode('9');
	BTNode* C = GreateNode('20');
	BTNode* D = GreateNode('15');
	BTNode* E = GreateNode('7');
	

	A->_left = B;
	A->_right = C;
	C->_left = D;
	C->_right = E;
	
	int depth = maxDepth(A);
	printf("该二叉树的深度是：%d", depth);
	
	return 0;
}

运行结果：

在这里插入图片描述

核心代码分析：

//二叉树的最大深度
int maxDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = maxDepth(root->_left);
	int rightDepth = maxDepth(root->_right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;

}

  • 当当前节点为NULL时（即到达叶子节点的子节点），返回深度 0。
    作用：防止无限递归，并为后续递归计算提供基准值。

  • 左子树深度：递归调用maxDepth(root->_left)计算左子树的最大深度。
    右子树深度：递归调用maxDepth(root->_right)计算右子树的最大深度。

  • 比较左右子树的深度，取较大值加 1（当前节点自身的深度）

最后的return它的作用是返回当前节点的最大深度；因为当前节点本身也算一层深度，所以需要在子树的最大深度基础上 +1

这个返回语句的本质是：当前节点的最大深度 = 左右子树的最大深度 + 1，通过递归回溯的方式从叶子节点向上逐层计算，最终得到整棵树的最大深度。

3.4翻转二叉树

在这里插入图片描述

  1. 前序遍历方法

思维流程图：
在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;

}BTNode;


//创建树
BTNode* GreateNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}

// 前序遍历打印树（用于验证）
void preOrderPrint(BTNode* root) 
{
	if (root == NULL)
	{
		return;
	}
	printf("%c ", root->_data);
	preOrderPrint(root->_left);
	preOrderPrint(root->_right);
}

//翻转一个二叉树
BTNode* flipTree(BTNode* root)
{
	if (root == NULL)
	{
		return NULL;
	}
	else
	{
		BTNode* tmp = root->_left;
		root->_left = root->_right;
		root->_right = tmp;

		flipTree(root->_left);
		flipTree(root->_right);

		return root;
	}
}

int main()
{
	BTNode* A = GreateNode('5');
	BTNode* B = GreateNode('7');
	BTNode* C = GreateNode('9');
	BTNode* D = GreateNode('8');
	BTNode* E = GreateNode('3');
	BTNode* F = GreateNode('2');
	BTNode* G = GreateNode('4');

	A->_left = B;
	A->_right = C;
	B->_left = D;
	B->_right = E;
	C->_left = F;
	C->_right = G;
	
	printf("原树前序遍历: \n");
	preOrderPrint(A);

	printf("\n");

	// 翻转二叉树
	BTNode* flippedRoot = flipTree(A);

	printf("翻转后树前序遍历: \n");
	preOrderPrint(flippedRoot);
	
	return 0;
}

运行结果：

在这里插入图片描述

  1. 中序遍历方法
BTNode* flipTree(BTNode* root)
{
	if (root == NULL)
	{
		return NULL;
	}
	else
	{
		BTNode* right = root->_right;//保存原始右子树指针
		root->_right = flipTree(root->_left);// 递归翻转左子树，并将结果赋给右子树
		root->_left = flipTree(right); // 递归翻转原始右子树（保存在right中），并将结果赋给左子树

		return root;
	}
}
  • 保存原始右子树：避免在递归过程中丢失右子树指针。
  • 翻转左子树：递归调用flipTree(root->_left)，并将返回的翻转后的左子树赋给当前节点的右子树。
  • 翻转右子树：递归调用flipTree(right)（原始右子树），并将返回的翻转后的右子树赋给当前节点的左子树。

🤔🤔🤔思考：为什么要返回root？

返回root的核心目的是维持树的结构连贯性：

  1. 递归连接子树：在递归调用中，需要将子树的根节点回给父节点，以便父节点能正确指向翻转后的子树。
    例如，当root->_right = flipTree(root->_left)时，flipTree(root->_left)返回的是翻转后的左子树的根节点，该节点需要被赋给当前节点的右子树指针。
  2. 统一接口：无论树的结构如何，函数始终返回当前处理节点的指针，使得递归调用可以嵌套进行。
  3. 避免断链：若不返回root，上层节点将无法得知子树的新根节点，导致树结构断裂。

3.5相同的树

在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;

}BTNode;

//创建树
BTNode* GreateNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->_data = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}

//相同的树
bool isSameTree(BTNode* p, BTNode* q)
{
	if (p == NULL && q == NULL)
	{
		return true;
	}
	//结构不同
	if (p == NULL && q != NULL)
	{
		return false;
	}
	//结构不同
	if (p != NULL && q == NULL)
	{
		return false;
	}
	//值不同
	if (p->_data != q->_data)
	{
		return false;
	}
	//比较左右子树
	return isSameTree(p->_left, q->_left) && isSameTree(p->_right, q->_right);
}

int main()
{
	BTNode* A = GreateNode('5');
	BTNode* B = GreateNode('7');
	BTNode* C = GreateNode('9');
	BTNode* D = GreateNode('5');
	BTNode* E = GreateNode('7');
	BTNode* F = GreateNode('9');
	//BTNode* G = GreateNode('4');

	
	A->_left = B;
	A->_right = C;
	
	D->_left = E;
	D->_right = F;
	
	bool result = isSameTree(A, D);
	printf("TreeA 和 TreeD 是否相同: %s\n", result ? "是" : "否");
	return 0;
}

运行结果：

在这里插入图片描述

3.6对称二叉树

在这里插入图片描述

// 辅助函数：递归判断两个子树是否镜像对称
bool isMirror(BTNode* t1, BTNode* t2) {
	if (t1 == NULL && t2 == NULL)
	{
		return true;
	}
	if (t1 == NULL || t2 == NULL)
	{
		return false;
	}

	return (t1->_data == t2->_data) && isMirror(t1->_left, t2->_right) && isMirror(t1->_right, t2->_left);
}



//判断二叉树是否轴对称
bool isSymmetric(BTNode* root)
{
	if (root == NULL)
	{
	 return true;
	}
	return isMirror(root->_left, root->_right);
}

3.7另一个树的子树

在这里插入图片描述

root跟subRoot中每一颗子树都进行比较，如果有相同的，则满足

//相同的树
bool isSameTree(BTNode* p, BTNode* q)
{
	if (p == NULL && q == NULL)
	{
		return true;
	}
	//结构不同
	if (p == NULL && q != NULL)
	{
		return false;
	}
	//结构不同
	if (p != NULL && q == NULL)
	{
		return false;
	}
	//值不同
	if (p->_data != q->_data)
	{
		return false;
	}
	//比较左右子树
	return isSameTree(p->_left, q->_left) && isSameTree(p->_right, q->_right);
}


//另一棵树的子树
bool isSubtree(BTNode* root, BTNode* subRoot)
{
    // 基准情况：如果主树root为空，显然不可能包含任何子树，返回false
	if (root == NULL)
	{
		return false;
	}

    // 检查当前节点为根的子树是否与subRoot完全相同
	if (isSameTree(root, subRoot))//判断里面用的是上面的函数
	{
		return true;
	}
	// 如果当前节点不匹配，则递归检查左子树和右子树
	return isSubtree(root->_left, subRoot) || isSubtree(root->_right, subRoot);
}

3.7平衡二叉树

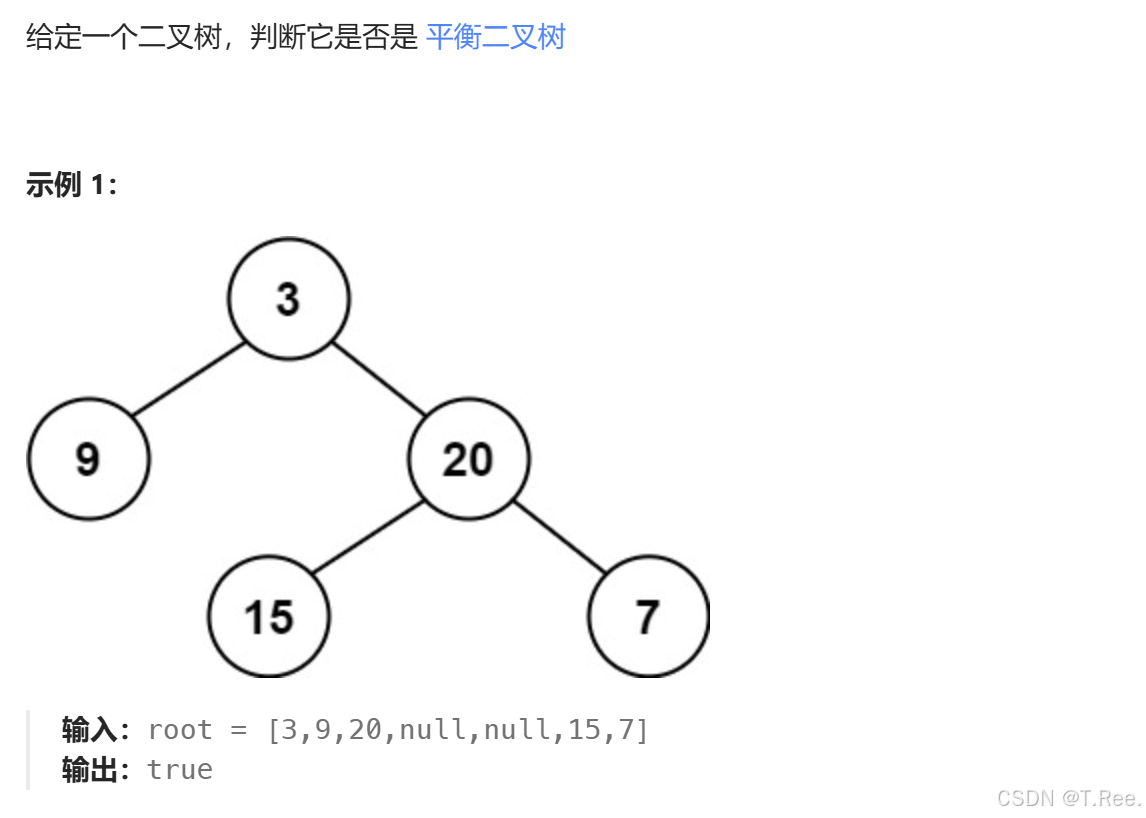
在这里插入图片描述

本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

前序方法：

//辅助函数
int TreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = TreeDepth(root->_left);//左树深度
	int rightDepth = TreeDepth(root->_right);//右树深度

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;

}

//平衡二叉树
bool isBalanced(BTNode* root) 
{
	if (root == NULL)
	{
		return true;
	}
	int gap = TreeDepth(root->_left) - TreeDepth(root->_right);
	
	if (abs(gap) > 1)//abs是求绝对值函数
	{
		return false;
	}

	return isBalanced(root->_left) && isBalanced(root->_right);
}

注意：为什么那个abs那里的if不要else呢？

  • 当abs(gap) <=1时，不要直接返回true，而是继续递归检查左右子树；
  • 将最后的递归检查移至if条件之后，确保当前节点平衡时，仍会检查其子树的平衡性。

逻辑流程:

1.如果当前节点为空，返回true。

2.计算左右子树的高度差gap：

  • 如果abs(gap) > 1，返回false（当前节点不平衡）。
  • 否则，递归检查左右子树是否平衡，并返回结果。

优化时间复杂度最好是O(n)；

后序方法：（优化了时间复杂度）

判断的同时把高度带给上一层的父亲

bool _isBalanced(BTNode* root ,int* pDepth)
{
	if (root == NULL)
	{
		*pDepth = 0;
		return true;
	}

	else
	{
		//判断左树，不满足
		int leftDepth = 0;
		if (_isBalanced(root->_left, &leftDepth ) == false)
		{
			return false;
		}

		//判断右树，不满足
		int rightDepth = 0; 
		if (_isBalanced(root->_right, &rightDepth) == false)
		{
			return false;
		}

		//判断当前树，不满足
		if (abs(leftDepth - rightDepth) > 1)
		{
			return false;
		}
		
		//满足
		*pDepth = leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
		return true;
	}
}

bool isBalanced(BTNode* root)
{
	int depth = 0;
	return _isBalanced(root, &depth);
}

main函数中调用：

// 调用isBalanced函数判断是否平衡
int balanced = isBalanced(A);

// 输出结果
if (balanced) 
{
	printf("这是一棵平衡二叉树。\n");
}
else 
{
	printf("这不是一棵平衡二叉树。\n");
}

这串代码中的*pDepth = leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;与计算最大深度的逻辑完全一致。这里的*pDepth同样是记录当前节点的最大深度，但其核心目的是为了辅助判断二叉树是否平衡。

这样优化后其实就类似于上面求深度的函数直接在里面写

举个例子：
在这里插入图片描述
总结：

方法一 简单直观，但存在大量重复计算，效率较低。
方法二 通过后序遍历和深度传递，将时间复杂度优化到 O (n)，是更优的解法。
建议：在实际应用中优先选择方法二，尤其是处理大规模数据时。

3.8重建二叉树

在这里插入图片描述

本题题意：这道题就说类似的把数组内容放到二叉树中通过前序遍历方法进行存储，也就是按照前序遍历的方法 照着数组内容进行存储；之前我们展开过二叉树遍历的数据，反过来就说 把数组里面的内容还原回去阿
在这里插入图片描述

//定义二叉树的节点结构
typedef struct TreeNode
{
	BTDataType _data;
	struct TreeNode* _left;
	struct TreeNode* _right;

}TreeNode;


//构建二叉树
TreeNode* CreateTree(char* str, int* pi)
{
	if (str[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	//不是#构建‘根’
	else
	{
		TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
		root->_data = str[*pi];

		(*pi)++;//因为前面那个i已经构建了

		root->_left = CreateTree(str, pi);
		root->_right = CreateTree(str,pi);

		return root;

	}
}

//中序遍历
void InOrder(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	InOrder(root->_left);
	printf("%c ", root->_data);
	InOrder(root->_right);

}


int main()
{
	char str[100];
	scanf("%s", str);//str数组名即首元素地址

	int i = 0;//下标
	TreeNode* root = CreateTree(str, &i);

	InOrder(root);

	return 0;
}

运行结果：

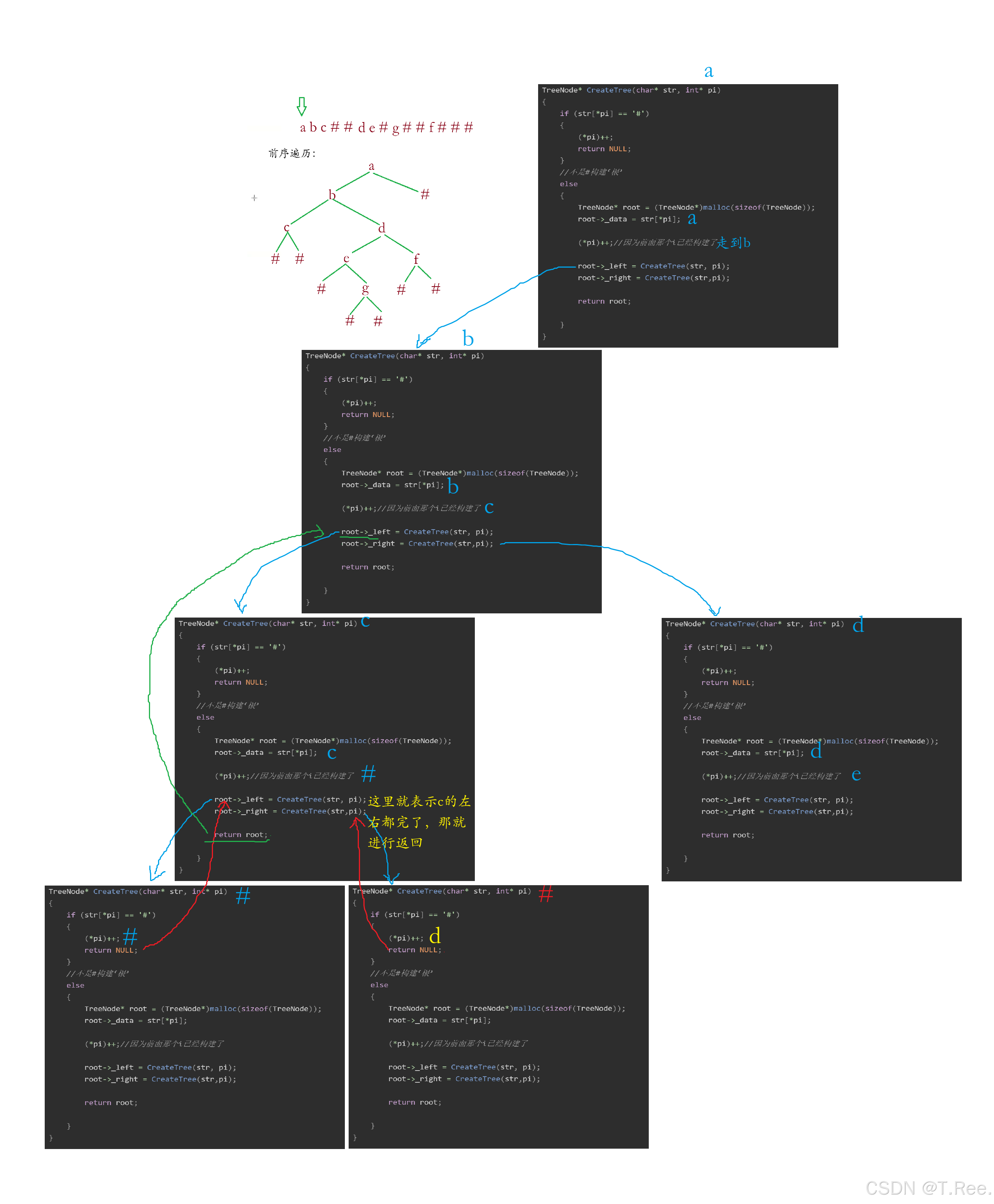
在这里插入图片描述
画图解析：
在这里插入图片描述
这里传指针是为了在同一个i上加加
CreateTree函数的工作流程是：

  • 检查当前字符是否为#，如果是则表示该节点为空，指针后移并返回 NULL
  • 如果不是#，则创建新节点并设置数据
  • 递归构建左子树和右子树
  • 返回构建好的节点

注意：这里的关键是使用指针pi来跟踪当前处理的字符位置，确保递归调用时位置信息能被正确传递和更新。

思考：🤔🤔🤔

为什么需要传递&i（地址）？

核心问题：递归函数需要在多层调用之间共享和修改同一个变量（即字符位置）。
每次递归调用都会创建独立的函数栈帧，其中的局部变量（包括参数）是相互独立的。如果直接传递int i，每次递归调用都会得到i的一个副本。当内层递归修改i时，外层递归的i值不会改变，导致所有递归调用都从同一位置开始解析字符串，最终造成无限循环或错误构建。（简单来讲呢就是：把数组里面的内容还原回去，首先要一个指针才能移动，从而指向数组里面不同的位置，实现遍历），通过传递&i，*pi指向的是主函数中的变量i，任何递归层对*pi的修改都会直接反映到这个共享变量上。

🎉🎉🎉
到这里本章就结束啦~
友友们
我们下期见咯~

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2378416.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

给图表组件上点“颜色” —— 我与 CodeBuddy 的合作记录

给图表组件上点“颜色” —— 我与 CodeBuddy 的合作记录

我正在参加CodeBuddy「首席试玩官」内容创作大赛&#xff0c;本文所使用的 CodeBuddy 免费下载链接&#xff1a;腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴 前段时间&#xff0c;我在开发一个 Vue3 项目的时候&#xff0c;碰到了一个小小的挑战&#xff1a;我想做一个可…
阅读更多...
使用 YOLO 结合 PiscTrace 实现股票走势图像识别

使用 YOLO 结合 PiscTrace 实现股票走势图像识别

在智能投研和金融分析中&#xff0c;自动识别图表中的模式&#xff08;如 K 线走势、支撑/阻力位、形态结构&#xff09;成为一种新兴手段。传统的技术分析依赖大量人工判断&#xff0c;而计算机视觉技术的发展&#xff0c;特别是 YOLO 模型在图像识别领域的高效表现&#xff0…
阅读更多...
OpenCV中的光流估计方法详解

OpenCV中的光流估计方法详解

文章目录 一、引言二、核心算法原理1. 光流法基本概念2. 算法实现步骤 三、代码实现详解1. 初始化设置2. 特征点检测3. 光流计算与轨迹绘制 四、实际应用效果五、优化方向六、结语 一、引言 在计算机视觉领域&#xff0c;运动目标跟踪是一个重要的研究方向&#xff0c;广泛应用…
阅读更多...
NBA足球赛事直播源码体育直播M33模板赛事源码

NBA足球赛事直播源码体育直播M33模板赛事源码

源码名称&#xff1a;体育直播赛事扁平自适应M33直播模板源码 开发环境&#xff1a;帝国cms7.5 空间支持&#xff1a;phpmysql 带软件采集&#xff0c;可以挂着自动采集发布&#xff0c;无需人工操作&#xff01; 演示地址&#xff1a;NBA足球赛事直播源码体育直播M33模板赛事…
阅读更多...
电子电器架构 --- 整车造车阶段四个重要节点

电子电器架构 --- 整车造车阶段四个重要节点

我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 钝感力的“钝”，不是木讷、迟钝，而是直面困境的韧劲和耐力，是面对外界噪音的通透淡然。 生活中有两种人，一种人格外在意别人的眼光;另一种人无论…
阅读更多...
黑马点评-用户登录

黑马点评-用户登录

文章目录 用户登录发送短信验证码注册/登录校验登录 用户登录 发送短信验证码 public Result sendCode(String phone, HttpSession session) {// 1.校验手机号if (RegexUtils.isPhoneInvalid(phone)) {// 2.如果不符合&#xff0c;返回错误信息return Result.fail("手机…
阅读更多...
十二、Hive 函数

十二、Hive 函数

作者&#xff1a;IvanCodes 日期&#xff1a;2025年5月1日 专栏&#xff1a;Hive教程 在数据处理的广阔天地中&#xff0c;我们常常需要对数据进行转换、计算、清洗或提取特定信息。Hive 提供了强大的内置运算符和丰富的内置函数库&#xff0c;它们就像魔法师手中的魔法棒&…
阅读更多...
No More Adam: 新型优化器SGD_SaI

No More Adam: 新型优化器SGD_SaI

一.核心思想和创新点 2024年12月提出的SGD-SaI算法&#xff08;Stochastic Gradient Descent with Scaling at Initialization&#xff09;本质上是一种在训练初始阶段对不同参数块&#xff08;parameter block&#xff09;基于**梯度信噪比&#xff08;g-SNR, Gradient Signa…
阅读更多...
JSP链接MySQL8.0（Eclipse+Tomcat9.0+MySQL8.0）

JSP链接MySQL8.0（Eclipse+Tomcat9.0+MySQL8.0）

所用环境 Eclipse Tomcat9.0 MySQL8.0.21(下载&#xff1a;MySQL Community Server 8.0.21 官方镜像源下载 | Renwole&#xff09; mysql-connector-java-8.0.21&#xff08;下载&#xff1a;MySQL :: Begin Your Download&#xff09; .NET Framework 4.5.2&#xff08;下…
阅读更多...
SEO长尾词与关键词优化实战

SEO长尾词与关键词优化实战

内容概要 在SEO优化体系中&#xff0c;长尾关键词与核心关键词的协同作用直接影响流量获取效率与用户转化路径。长尾词通常由3-5个词组构成&#xff0c;搜索量较低但意图明确&#xff0c;能精准触达细分需求用户&#xff1b;核心关键词则具备高搜索量与广泛覆盖能力&#xff0…
阅读更多...
机器学习-人与机器生数据的区分模型测试-数据处理1

机器学习-人与机器生数据的区分模型测试-数据处理1

附件为训练数据&#xff0c;总体的流程可以作为参考。 导入依赖 import pandas as pd import os import numpy as np from sklearn.model_selection import train_test_split,GridSearchCV from sklearn.ensemble import RandomForestClassifier,VotingClassifier from skle…
阅读更多...
HelloWorld

HelloWorld

HelloWorld 新建一个java文件 文件后缀名为 .javahello.java【注意】系统可能没有显示文件后缀名&#xff0c;我们需要手动打开 编写代码 public class hello {public static void main(String[] args) {System.out.print(Hello,World)} }编译 javac java文件&#xff0c;会生…
阅读更多...
SEO 优化实战：ZKmall模板商城的 B2C商城的 URL 重构与结构化数据

SEO 优化实战：ZKmall模板商城的 B2C商城的 URL 重构与结构化数据

在搜索引擎算法日益复杂的今天&#xff0c;B2C商城想要在海量信息中脱颖而出&#xff0c;仅靠优质商品和营销活动远远不够。ZKmall模板商城以实战为导向&#xff0c;通过URL 重构与结构化数据优化两大核心策略&#xff0c;帮助 B2C 商城实现从底层架构到搜索展示的全面升级&…
阅读更多...
数字万用表与指针万用表使用方法及注意事项

数字万用表与指针万用表使用方法及注意事项

在电子测量领域&#xff0c;万用表是极为常用的工具&#xff0c;数字万用表和指针万用表各具特点。熟练掌握它们的使用方法与注意事项&#xff0c;能确保测量的准确性与安全性。下面为您详细介绍&#xff1a; 一 、数字万用表按钮功能 > 进入及退出手动量程模式 每 按 […
阅读更多...
【读代码】端到端多模态语言模型Ultravox深度解析

【读代码】端到端多模态语言模型Ultravox深度解析

一、项目基本介绍 Ultravox是由Fixie AI团队开发的开源多模态大语言模型，专注于实现音频-文本的端到端实时交互。项目基于Llama 3、Mistral等开源模型，通过创新的跨模态投影架构，绕过了传统语音识别（ASR）的中间步骤，可直接将音频特征映射到语言模型的高维空间。 核心优…
阅读更多...
RabbitMQ工作流程及使用方法

RabbitMQ工作流程及使用方法

一、什么是RabbitMQ RabbitMQ 是一款基于 ‌AMQP&#xff08;高级&#xff0c;消息队列协议&#xff09;‌ 的开源消息中间件&#xff0c;专为分布式系统设计&#xff0c;用于实现应用程序间的异步通信&#xff0c;其核心功能是通过 ‌消息代理&#xff08;Message Broker&…
阅读更多...
算法：分治法

算法：分治法

实验内容 在一个2kⅹ2k个方格组成的棋盘中&#xff0c;若恰有一个方格与其他方格不同&#xff0c;则称该方格为特殊方格&#xff0c;且称该棋盘为一特殊棋盘。 显然&#xff0c;特殊方格出现的位置有4k 种情况&#xff0c;即k>0,有4k 种不同的特殊棋盘 棋盘覆盖&#xff1a…
阅读更多...
MySQL初阶：sql事务和索引

MySQL初阶：sql事务和索引

索引&#xff08;index&#xff09; 可以类似理解为一本书的目录&#xff0c;一个表可以有多个索引。 索引的意义和代价 在MySQL中使用select进行查询时会经过&#xff1a; 1.先遍历表 2.将条件带入每行记录中进行判断&#xff0c;看是否符合 3.不符合就跳过 但当表中的…
阅读更多...
docker部署第一个Go项目

docker部署第一个Go项目

1.前期准备 目录结构 main.go package mainimport ("fmt""github.com/gin-gonic/gin""net/http" )func main() {fmt.Println("\n .::::.\n .::::::::.\n :::::::::::\n …
阅读更多...
Visual Studio2022跨平台Avalonia开发搭建

Visual Studio2022跨平台Avalonia开发搭建

由于我已经下载并安装了 VS2022版本&#xff0c;这里就跳过不做阐述。 1.安装 Visual Studio 2022 安装时工作负荷Tab页勾选 ‌“.NET 桌面开发”‌ 和“Visual Studio扩展开发”‌ &#xff0c;这里由于不是用的微软的MAUI&#xff0c;所以不用选择其他的来支持跨平台开发&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023