常见激活函数——作用、意义、特点及实现

news2025/7/11 10:11:44

文章目录

激活函数的意义
常见激活函数及其特点
- 1. Sigmoid（Logistic 函数、S型函数）
- 2. Tanh（双曲正切函数）
- 3. ReLU（Rectified Linear Unit修正线性单元）
- 4. Softmax
- 5. Swish（Google 提出）
python实现各类激活函数

激活函数（Activation Function）是神经网络中的核心组件之一，它决定了神经元的输出方式，**直接影响模型的非线性表达能力、梯度传播和训练效果。**不同的激活函数适用于不同的场景，选择合适的激活函数对模型性能至关重要。在一些模型训练中会涉及到激活函数的选择，今天自己查阅资料时总结一下不同激活函数的作用、意义、特点及如何实现。

“激活函数”（Activation Function，也常被译为“激励函数”）的作用就是为了给神经网络加入非线性的表达能力，它改进了阈值函数只能单纯比较大小判断是否激发神经元信号的简单逻辑，允许根据实际需要，对输入的加权和进行不受限制的数学处理。
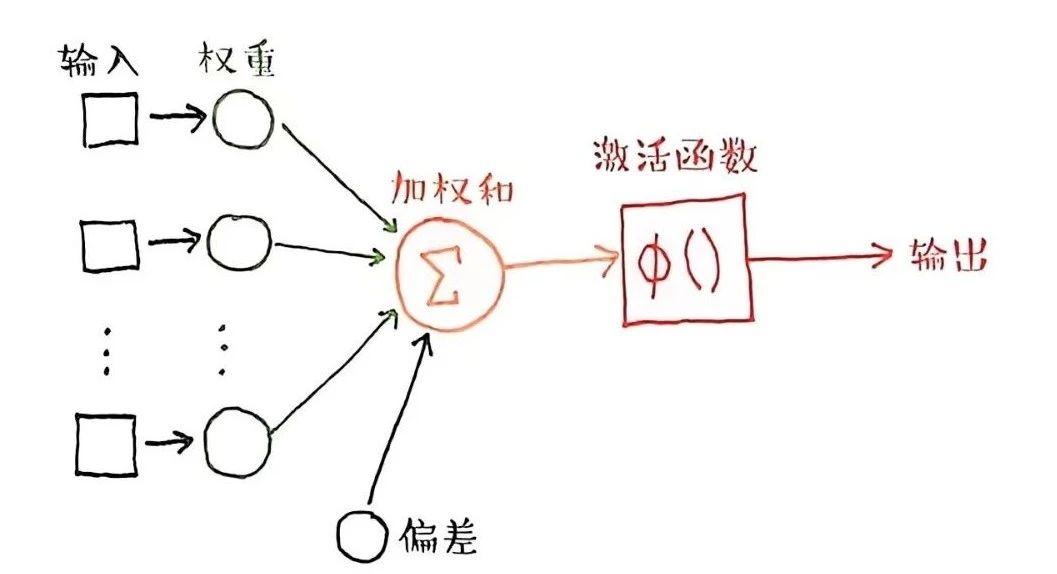
在这里插入图片描述

——周志明《智慧的疆界：从图灵机到人工智能》

一些高质量的文章可供学习
神经网络|(十二)|常见激活函数
图解深度学习中的激活函数

激活函数的意义

引入非线性

突破线性模型限制：如果神经网络中没有激活函数，每一层都只是线性变换，无论网络有多少层，其输出都是输入的线性组合，无法逼近复杂函数。而激活函数可以引入非线性因素，使神经网络能够学习和表达复杂的非线性关系，从而解决诸如图像识别、语音识别等复杂任务。
构造复杂决策边界：激活函数的非线性映射可以使神经网络构造出复杂的决策边界，提高模型的泛化能力，使其能够更好地拟合数据分布，区分不同类别的数据。

控制输出值范围

归一化输出：某些激活函数如sigmoid会将输出限制在特定区间内，如(0,1)，tanh的输出范围是(-1,1)，这有助于提高网络训练稳定性，并减少梯度爆炸或梯度消失的风险，方便后续处理和计算。
便于概率解释：在二分类问题中，sigmoid函数的输出可以被解释为概率，方便对模型的预测结果进行理解和分析。

影响梯度传播

缓解梯度消失或爆炸问题：不同的激活函数对梯度的传播有不同的影响。例如，relu函数在正区间梯度恒为1，有效缓解了sigmoid和tanh的梯度消失问题，加快了模型的收敛速度；而tanh函数虽然也存在梯度消失问题，但其输出以零为中心，有助于改善梯度下降的效率和网络的收敛速度。
优化训练过程：激活函数的选择会影响反向传播中的梯度计算，从而影响网络的训练效率。合适的激活函数可以使梯度传播更加稳定和有效，

加快模型的训练速度，提高训练效果。
增加网络稀疏性

减少计算量：以relu函数为例，它将输入小于0的部分置为0，大于0的部分保持不变，使得部分神经元输出为0，增加了网络的稀疏性。这可以减少计算量，提高计算效率，特别是在处理大规模数据和深度网络时，这种稀疏性可以显著降低计算成本。
提取关键特征：网络的稀疏性有助于提取更具有区分性的特征，使模型更加关注重要的输入特征，提高模型的性能和泛化能力。

常见激活函数及其特点

在这里插入图片描述

1. Sigmoid（Logistic 函数、S型函数）

在这里插入图片描述

2. Tanh（双曲正切函数）

在这里插入图片描述

3. ReLU（Rectified Linear Unit修正线性单元）

在这里插入图片描述

4. Softmax

在这里插入图片描述

5. Swish（Google 提出）

在这里插入图片描述

python实现各类激活函数

import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# Sigmoid
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Tanh
def tanh(x):
    return np.tanh(x)

# ReLU
def relu(x):
    return np.maximum(0, x)

# Leaky ReLU
def leaky_relu(x, alpha=0.01):
    return np.where(x > 0, x, alpha * x)

# Softmax
def softmax(x):
    exp_x = np.exp(x - np.max(x))  # 防止数值溢出
    return exp_x / exp_x.sum(axis=0)

# Swish
def swish(x, beta=1.0):
    return x * sigmoid(beta * x)

# 测试数据
x = np.linspace(-5, 5, 100)

# 计算各激活函数输出
y_sigmoid = sigmoid(x)
y_tanh = tanh(x)
y_relu = relu(x)
y_leaky_relu = leaky_relu(x)
y_softmax = softmax(x)
y_swish = swish(x)

# 绘制图像
plt.figure(figsize=(12, 8))

plt.subplot(2, 3, 1)
plt.plot(x, y_sigmoid, label="Sigmoid")
plt.title("Sigmoid")
plt.grid()

plt.subplot(2, 3, 2)
plt.plot(x, y_tanh, label="Tanh", color="orange")
plt.title("Tanh")
plt.grid()

plt.subplot(2, 3, 3)
plt.plot(x, y_relu, label="ReLU", color="green")
plt.title("ReLU")
plt.grid()

plt.subplot(2, 3, 4)
plt.plot(x, y_leaky_relu, label="Leaky ReLU", color="red")
plt.title("Leaky ReLU")
plt.grid()

plt.subplot(2, 3, 5)
inputs = np.vstack([x, 0.5 * x, 0.2 * x])
# 计算Softmax输出
# Softmax计算三个变量各自所占的比例
outputs = softmax(inputs)
for i in range(outputs.shape[0]):
    plt.plot(x, outputs[i], label=f'变量 {i+1}所占比例')
plt.title("Softmax")
plt.legend() 
plt.grid()

plt.subplot(2, 3, 6)
plt.plot(x, y_swish, label="Swish", color="purple")
plt.title("Swish")
plt.grid()

plt.tight_layout()
plt.show()