提示:100道LeetCode热题-8-5主要是二叉树相关,包括三题:路径总和 III、二叉树的最近公共祖先、二叉树中的最大路径和。由于初学,所以我的代码部分仅供参考。
前言
二叉树完结撒花~
下一次的图论会是一些有趣的应用案例~
提示:以下是本篇文章正文内容,下面结果代码仅供参考
题目1:路径总和 III
1.题目要求:
题目如下:
给定一个二叉树的根节点
root,和一个整数targetSum,求该二叉树里节点值之和等于targetSum的 路径 的数目。路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
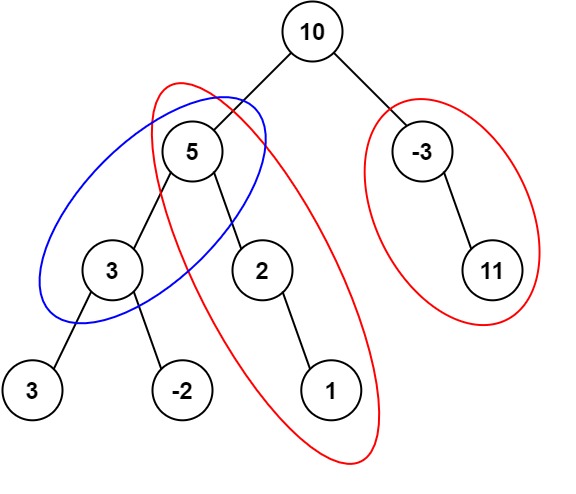
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3提示:
- 二叉树的节点个数的范围是
[0,1000]-<= Node.val <=
-1000 <= targetSum <= 1000
代码框架已经提供如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def pathSum(self, root, targetSum):
"""
:type root: Optional[TreeNode]
:type targetSum: int
:rtype: int
2.结果代码:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def pathSum(self, root, targetSum):
"""
:type root: Optional[TreeNode]
:type targetSum: int
:rtype: int
"""
from collections import defaultdict
def dfs(node, cur_sum):
if not node:
return 0
cur_sum += node.val
# 检查是否存在前缀和为 cur_sum - targetSum 的路径
path_count = prefix_sum_count[cur_sum - targetSum]
# 更新当前前缀和的出现次数
prefix_sum_count[cur_sum] += 1
# 递归处理左子树和右子树
path_count += dfs(node.left, cur_sum)
path_count += dfs(node.right, cur_sum)
# 回溯,恢复哈希表状态
prefix_sum_count[cur_sum] -= 1
return path_count
# 初始化前缀和哈希表
prefix_sum_count = defaultdict(int)
prefix_sum_count[0] = 1 # 前缀和为 0 的路径出现次数为 1
return dfs(root, 0)说明:
-
问题难点:
-
路径不需要从根节点开始,也不需要在叶子节点结束。
-
需要统计所有满足条件的路径,而不仅仅是从根到叶子的路径。
-
-
前缀和的应用:
-
使用前缀和可以快速判断从某个节点到其祖先节点的路径和是否等于目标值。
-
通过哈希表(字典)记录前缀和的出现次数,可以快速查找是否存在满足条件的路径。
-
-
深度优先搜索(DFS):
-
遍历二叉树的每个节点,从每个节点出发,计算以该节点为起点的路径和。
-
使用递归的方式,分别处理左子树和右子树。
-
当然,这个代码只是一种解决方法,还有更多更优方案等你来想~

题目2:二叉树的最近公共祖先
1.题目要求:
题目如下:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点5和节点4的最近公共祖先是节点5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1提示:
- 树中节点数目在范围
[2,内。]
-<= Node.val <=
- 所有
Node.val互不相同。p != qp和q均存在于给定的二叉树中。
代码框架已经提供如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
2.结果代码:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if not root or root == p or root == q:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left and right:
return root
return left if left else right说明:
递归逻辑还是清晰的:
-
递归地在左子树和右子树中查找
p和q。 -
如果左子树和右子树的返回值都不为空,说明
p和q分别在左右子树中,当前节点就是它们的最近公共祖先。 -
如果左子树或右子树的返回值不为空,返回不为空的那个子树的结果。
复杂度:
-
时间复杂度:O(n),其中 n 是二叉树的节点数。每个节点最多被访问一次。
-
空间复杂度:O(h),其中 h 是二叉树的高度,主要取决于递归调用栈的深度。

题目3:二叉树中的最大路径和
1.题目要求:
题目如下:
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点
root,返回其 最大路径和 。示例 1:
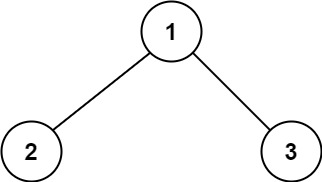
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6示例 2:
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42提示:
- 树中节点数目范围是
[1, 3 *]
-1000 <= Node.val <= 1000
代码框架已经提供如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def maxPathSum(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
2.结果代码:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def maxPathSum(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
self.maxSum = -100000
def dfs(root):
if not root: return 0
l_max = max(dfs(root.left), 0)
r_max = max(dfs(root.right), 0)
cur_max = root.val + l_max + r_max
if cur_max > self.maxSum: self.maxSum = cur_max
# dfs(root.left)
# dfs(root.right)
return root.val + max(l_max, r_max)
dfs(root)
return self.maxSum说明:
这个有参考别人的一些代码,简单解释一下初始化 self.maxSum 的值:
在代码中,self.maxSum 被初始化为 -100000,而不是 float('-inf')。题目已经给出了节点值的范围是 [−1000,1000],因此最大路径和的最小可能值不会低于 -100000(假设树中有 100 个节点,每个节点值为 -1000)。

总结
针对二叉树的三种题型进行了学习,了解了部分有关二叉树与python的相关知识,坚持就是胜利,大家加油!