杆件的拉伸与压缩

第一题

$$\mathcal{Q}uestion$$

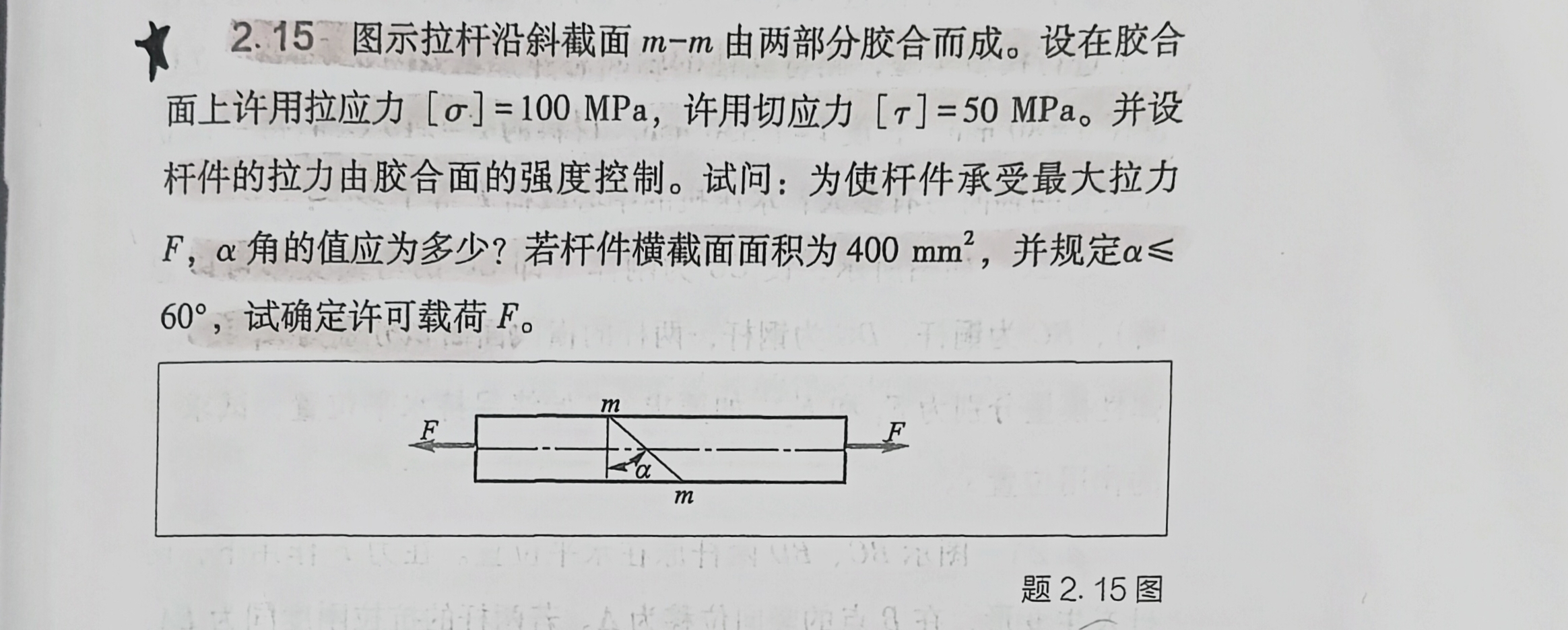
图示拉杆沿斜截面$m-m$由两部分胶合而成。设在胶合面上许用拉应力$[\sigma ]=100\text{MPa}$，许用切应力$[\tau ]=50\text{MPa}$。并设杆件的拉力由胶合面的强度控制。试问：

1. 为使杆件承受最大拉力$F$，$\alpha$角的值应为多少？
2. 若杆件横截面面积为$400{\text{mm}}^2$，并规定$\alpha \le 60^{\circ }$，试确定许可载荷$F$。

$$\mathcal{A}nswer$$

由拉伸杆斜截面上的应力公式：
$$\begin{array}{c}{\sigma }_{\alpha }=\frac{F}{A}{\cos }^2\alpha \end{array}$$
$$\begin{array}{c}{\tau }_{\alpha }=\frac{F}{A}\sin \alpha \cos \alpha \end{array}$$
该问题转化为以下最优化问题：
$$\max F$$
$$\begin{array}{rl}& \text{s.t.}\{\begin{array}{l}{\sigma }_{\alpha }=\frac{F}{A}{\cos }^2\alpha \le [\sigma ]\\ {\tau }_{\alpha }=\frac{F}{A}\sin \alpha \cos \alpha \le [\tau ]\end{array}\end{array}$$

在问题一的背景下：

$${\alpha }_0=\arctan \frac{[\tau ]}{[\sigma ]}=26.6^{\circ }$$

在问题二的背景下：

$$F_{\max }=\frac{A[\sigma ]}{{\cos }^2{\alpha }_0}=50\text{kN}$$

第二题

$$\mathcal{Q}uestion$$
重量为$W$ 的均质圆形等截面空心长钢杆，长度为$l$，内径为$d$，外径为 $D$。施工的某一过程中需要将其竖直悬吊于空中。若材料的弹性模量为$E$，试求此时杆件在自重作用下的伸长量 $\Delta l$。

$$\mathcal{A}nswer$$
取微元，其受轴力：

$$F_N(x)=\frac{W}{l}(l-x)$$
由胡克定律：

$$\text{d}(\delta l)=\frac{F_N\text{d}x}{EA}$$

两边同时积分得到：
$${\int }_L\text{d}(\delta l)={\int }_0^l\frac{F_N\text{d}x}{EA}$$
故
$$\Delta l=\frac{2lW}{E\pi \left(D^2-d^2\right)}$$

第三题

$$\mathcal{Q}uestion$$

在图示杆系中，$BC$和$BD$两杆的材料相同，且抗拉和抗压许用应力相等，同为$[\sigma ]$。为使杆系使用的材料最省，试求夹角$\theta$的值。

$$\mathcal{A}nswer$$

首先，分析 $B$ 铰链的受力，根据平衡条件：
$$\{\begin{array}{ll}\sum F_x=0,& F_{N2}-F_{N1}\cos \theta =0\\ \sum F_y=0,& F_{N1}\sin \theta -F=0\end{array}$$
解上述两式可得：
$$F_{N1}=\frac{F}{\sin \theta },F_{N2}=F\cot \theta$$
最合理的情况是两杆同时达到许用应力值，即：
$${\sigma }_1=\frac{F_{N1}}{A_1}=[\sigma ],{\sigma }_2=\frac{F_{N2}}{A_2}=[\sigma ]$$
将 $F_{N1}$、$F_{N2}$ 表达式代入上式，可得 $BD$、$BC$ 杆的截面面积分别为：
$$A_1=\frac{F}{\sin \theta [\sigma ]},A_2=\frac{F\cot \theta }{[\sigma ]}$$
结构的体积为：
$$\begin{array}{rl}V& =A_1{L}_1+A_2{L}_2\\ & =\frac{Fl}{\sin \theta [\sigma ]\cos \theta }+\frac{Fl\cos \theta }{\sin \theta [\sigma ]}\\ & =\frac{Fl}{[\sigma ]}\left(\frac{1+{\cos }^2\theta }{\sin \theta \cos \theta }\right)\\ & =\frac{Fl}{[\sigma ]}\left(\frac{{\sin }^2\theta +2{\cos }^2\theta }{\sin \theta \cos \theta }\right)\\ & =\frac{Fl}{[\sigma ]}(\tan \theta +2\cot \theta )\end{array}$$
对体积 $V$ 求导，体积最小的条件是：
$$\frac{dV}{d\theta }=\frac{Fl}{[\sigma ]}\left(\frac{1}{{\cos }^2\theta }-\frac{2}{{\sin }^2\theta }\right)=\frac{Fl}{[\sigma ]}\left(\frac{{\sin }^2\theta -2{\cos }^2\theta }{{\sin }^2\theta {\cos }^2\theta }\right)=0$$
解上式得：
$$2{\cos }^2\theta -{\sin }^2\theta =0⟹{\tan }^2\theta =2⟹\theta =54.7^{\circ }$$
所以，使杆系使用材料最省的夹角为 $\theta =54.7^{\circ }$。