c++——二叉树进阶

1. 内容安排说明

二叉树在前面C数据结构阶段已经讲过，本节取名二叉树进阶是因为：

1. map和set特性需要先铺垫二叉搜索树，而二叉搜索树也是一种树形结构

2. 二叉搜索树的特性了解，有助于更好的理解map和set的特性

3. 二叉树中部分面试题稍微有点难度，在前面讲解大家不容易接受，且时间长容易忘

4. 有些OJ题使用C语言方式实现比较麻烦，比如有些地方要返回动态开辟的二维数组，非常麻烦。因此本节借二叉树搜索树，对二叉树部分进行收尾总结。

2. 二叉搜索树实现

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

1若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

2若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

3它的左右子树也分别为二叉搜索树

2.1二叉搜索树操作

接下来我们对于搜索二叉树的分析都是基于这个树来进行的

1二叉树的搜索

Node* Find(const K& key)
{
	if (_root->_key == key)
	{
		return _root;
	}
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			cur = cur->_left;
		}
		else
		{
			return cur;
		}
	}
	return nullptr;
}

2二叉树的构建

bool Insert(const K& key)
{
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	//先找到符合的位置，再进行插入
	Node* prev = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			prev = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			prev = cur;
			cur = cur->_left;
		}
		else
		{
			return false;//搜索二叉树不允许重复
		}
	}
	//这时候找到位置了进行链接
	cur = new Node(key);
	if (prev->_key < key)
	{
		prev->_right = cur;
	}
	else
	{
		prev->_left = cur;
	}
	return true;

}

3二叉树的删除

这里的删除分为三个场景

1删除的节点为叶子节点（没有子节点）（这里直接删除就行了）

2删除的节点有一个子节点

3删除的节点有两个子节点

这里就要用到替换法（左树的最大节点或者右树的最小节点）

具体代码：


		bool Erase(const K& key)
		{
			//这里要保留parent 就不复用Find函数了
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else//找到了
				{
					//接下来根据各个场景依次判断
					//如果左右其中一个为空，那么属于第一类，直接将空的另一边连接到parent

					//左为空
					if (cur->_left == nullptr)
					{
						if (cur == _root)//防止parent为空
						{
							_root = cur->_right;
						}
						else
						{
							if (parent->_key < cur->_key)
							{
								parent->_right = cur->_right;

							}
							else
							{
								parent->_left = cur->_right;
							}
						}

					}//右为空
					else if (cur->_right == nullptr)
					{
						if (cur == _root)//防止parent为空
						{
							_root = cur->_left;
						}
						else
						{
							if (parent->_key < cur->_key)
							{
								parent->_right = cur->_left;

							}
							else
							{
								parent->_left = cur->_left;
							}
						}
					}
					else//左右都不为空,我们找左树最大的来替代
					{
						parent = cur;//防止parent 为空
						Node* LeftMax = cur->_left;
						while (LeftMax->_right)
						{
							parent = LeftMax;
							LeftMax = LeftMax->_right;
						}
						//找到最大的就替换
						cur->_key = LeftMax->_key;
						//再将这个节点删除,这个节点可能有左树
						if (LeftMax == cur->_left)
						{
							parent->_left = LeftMax->_left;
						}
						else//这时候要特殊处理
						{
							parent->_right = LeftMax->_left;
						}
						cur = LeftMax;

					}
					delete cur;
					return true;
				}

			}
			//没找到
			return false;

		}

接下来我们用递归实现二叉搜索树的递归版本

1查找

public:
	//递归版本的查找
	Node* FindR(const K& key)
	{
		return _FindR(_root, key);
	}
private:
Node* _FindR(Node* root,const K& key)
{
	if (root == nullptr)
	{
		return nullptr;
	}

	if (root->_key == key)
	{
		return root;
	}
	else if (root->_key < key)
	{
		return _FindR(root->_right, key);
	}
	else
	{
		return _FindR(root->_left, key);
	}
	
}

2插入

插入这里就要讲的很多了，这里_InsertR用的是引用返回（这是指针和引用的结合）,这就给我们省下了很多力气，因为不用再去判断这个节点是parent 的左树还是右树

public:	
//递归版本的插入
	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}
private:
		bool _InsertR(Node* &root, const K& key)
		{
			if (root == nullptr)
			{
				//这时候要注意，指针加引用很厉害
				root = new Node(key);
				return true;
			}
			if (root->_key < key)
			{
				_InsertR(root->_right, key);
			}
			else if (root->_key > key)
			{
				_InsertR(root->_left, key);
			}
			else
			{
				return false;
			}

		}

3删除

bool _EraseR(Node*& root, const K& key)
{
	if (root == nullptr)
	{
		return false;
	}
	//要转化为子问题分置
	if (root->_key < key)
	{
		_EraseR(root->_right, key);
	}
	else if (root->_key > key)
	{
		_EraseR(root->_left, key);
	}
	else //找到了
	{
		Node* del = root;
		if (root->_left == nullptr)
		{
			root = root->_right;
		}
		else if (root->_right == nullptr)
		{
			root = root->_left;
		}
		else //3左右都不为空
		{
			Node* leftMax = root->_left ;
			while (leftMax->_right)
			{
				leftMax = leftMax->_right;
			}
			swap(leftMax->_key, root->_key);
			//这一步很精髓
			return _EraseR(root->_left, key);
            这里一定是返回了，不然还会走下面删除，就删除多了
		}
		delete del;
		return true;
	}
}

这里最后_EraseR的时候不能传leftMax，因为传leftMax有些情况删不掉

以上三个基本的完成了，剩下的destory走一个后续删除就可以了

3.二叉树搜索树应用分析

二叉搜索树在实际应用当中很常见

有两个模型

1key的搜索模型：快速判断不在的场景

门禁系统，小区车辆出入系统

2，key.value的搜索模型：通过一个值，去找另外一个值

商场的车辆出入系统模型（车牌号和入场时间联系起来）

4. 二叉树进阶面试题

606. 根据二叉树创建字符串 - 力扣（LeetCode）

这一题根本就是前序

要注意

1当左树为空，右树为空，都不加括号

2左树不为空，右树为空，右树不加括号

3左树为空，右树不为空，左树加括号

class Solution {
public:
    string tree2str(TreeNode* root) {
        
        if(root==nullptr)
        {
            return "";
        }
        string str=to_string(root->val);
        if(root->left || root->right)
        {
            str+="(";
            str+=tree2str(root->left);
            str+=")";
        }
        if(root->right)
        {
            str+="(";
            str+=tree2str(root->right);
            str+=")"; 
        }
 
        return str;
    }
};

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

class Solution {
public:
    bool Find(TreeNode* root,int val)
    {
        if(root==nullptr)
        return false;
        if(root->val==val)
        return true;

        return Find(root->left,val) || Find(root->right,val);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr)
        return nullptr;
        if(p==root || q == root)
        {
            return root;
        }
        bool pleft,pright,qleft,qright;
        pleft = Find(root->left,p->val);
        pright = !pleft;
        qleft = Find(root->left,q->val);
        qright = !qleft;
        if(pleft && qleft)
        {
            return lowestCommonAncestor( root->left,  p,  q);
        }
        else if(pright && qright)
        {
            return lowestCommonAncestor( root->right,  p,  q);
        }
        else
        {
            return root;
        }
    }

    
};

这里的解法就是暴力求解，我们可以优化解法让它达到O（N）

就是如果能倒着走，就可以转化为链表相交

这里就用一个栈来实现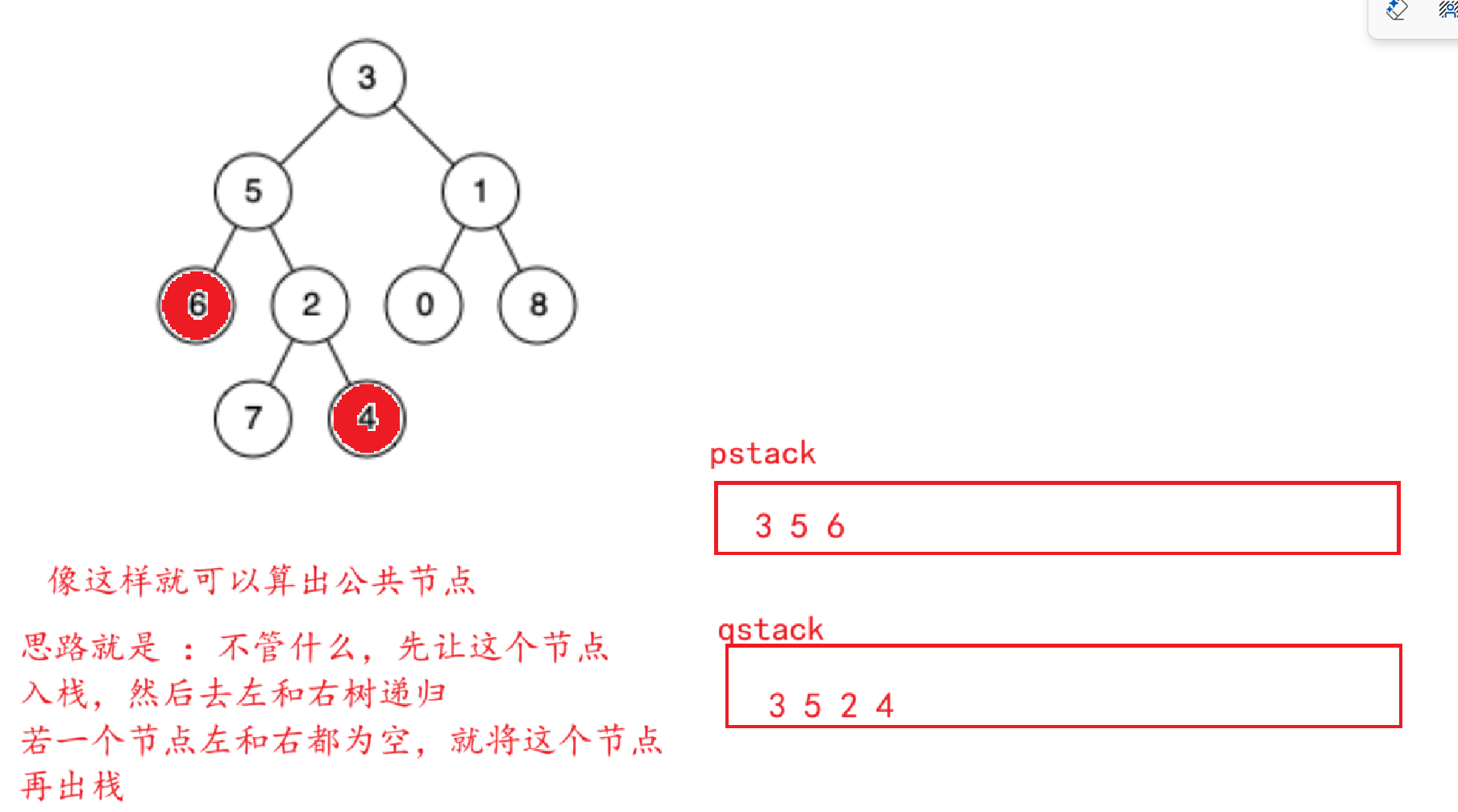

class Solution {
public:
    bool CreatStack(TreeNode* root,stack<TreeNode*>& st,TreeNode* x)
    {
        if(root==nullptr)
            return false;

        st.push(root);
        if(root==x)
        {
            return true;
        }
        //左右两边找到了就返回
       if(CreatStack(root->left,st,x))
            return true;
        if(CreatStack(root->right,st,x))
            return true;

        st.pop();
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> pstack,qstack;
        CreatStack(root,pstack,p);
        CreatStack(root,qstack,q);

        while(pstack.size()>qstack.size())
        {
            pstack.pop();
        }
        while(pstack.size()<qstack.size())
        {
            qstack.pop();
        }
        while(pstack.top()!=qstack.top())
        {
            pstack.pop();
            qstack.pop();
        }
        return pstack.top();
    }
};

二叉搜索树与双向链表_牛客题霸_牛客网

这种写法是实在写不出来就这样写

class Solution {
public:
	void Inorder(TreeNode* root,vector<TreeNode*> &v)
	{
		if(root==nullptr)
		{
			return ;
		}
		Inorder(root->left,v);
		v.push_back(root);

		Inorder(root->right,v);
	}

    TreeNode* Convert(TreeNode* pRootOfTree) {
		if(pRootOfTree==nullptr)
		{
			return nullptr;
		}
        vector<TreeNode*> vt;
		Inorder(pRootOfTree,vt);
		TreeNode* root = vt[0];
		TreeNode* end = vt[vt.size()-1];
		root->right = vt[1];
		end->left = vt[vt.size()-2];
		for(size_t i  = 1;i<vt.size()-1;i++)
		{
			vt[i]->left = vt[i-1];
			vt[i]->right = vt[i+1];
		}
		root->left = nullptr;
		end->right = nullptr;
		return root;
    }
};

这个才是正解

class Solution {
public:
	void _Convert(TreeNode* cur,TreeNode* &prev)
	{
		if(cur==nullptr)
		{
			return ;
		}

		_Convert(cur->left,prev);
		//中序
		cur->left = prev;
		if(prev)
		{
			prev->right = cur;
		}
		prev = cur;
		_Convert(cur->right,prev);
	}

    TreeNode* Convert(TreeNode* pRootOfTree) {
		if(pRootOfTree ==nullptr)
		{
			return nullptr;
		}
        TreeNode* head = pRootOfTree;
		TreeNode* prev = nullptr;
		while(head->left)
		{
			head = head->left;
		}
		_Convert(pRootOfTree, prev);
		head->left==nullptr;
		return head;
    }
};

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

前序：根左子树右子树

中序：左子树根右子树

class Solution {
public:
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,
    int& i,int begin,int end)
    {
        if(begin>end)
        {
            return nullptr;
        }
        //建立根节点
        TreeNode* root = new TreeNode(preorder[i]);
        //查找根节点位置，分出左右区间
        int rooti = begin;
        while(rooti<=end)
        {
            if(preorder[i]==inorder[rooti])
            {
                break;
            }
            rooti++;
        }
        i++;
        //区间就是[begin,rooti-1]rooti[rooti+1,end]
        root->left = _buildTree(preorder,inorder,i,begin,rooti-1);
        root->right = _buildTree(preorder,inorder,i,rooti+1,end);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        
        int i = 0;
        int begin = 0;
        int end = inorder.size()-1;
        TreeNode* root = _buildTree(preorder,inorder,i,begin,end);
        return root;
    }
};

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

这两题就差不多，就是后续的时候倒着遍历posorder

class Solution {
public:
    TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int& posi,int begin ,int end)
    {
        if(begin>end)
        {
            return nullptr;
        }
        TreeNode* root = new TreeNode(postorder[posi]);
        int rooti = begin;
        while(rooti<=end)
        {
            if(inorder[rooti]==postorder[posi])
                break;
                
            rooti++;
        }
        posi--;
        root->right = _buildTree(inorder,postorder,posi,rooti+1,end);
        root->left = _buildTree(inorder,postorder,posi,begin,rooti-1);
        return root;

    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int posi = postorder.size()-1;
        int begin = 0;
        int end = inorder.size()-1;
        TreeNode* root = _buildTree(inorder,postorder,posi,begin,end);
        return root;
    }
};

144. 二叉树的前序遍历 - 力扣（LeetCode）

这个要求是非递归实现，这就与我们之前搞的不同了，递归实现很简单，非递归就是用迭代的方式来实现

class Solution {
public:
    
    vector<int> preorderTraversal(TreeNode* root) {
        
        TreeNode* cur = root;
        stack<TreeNode*> st;
        vector<int> v;
        while(cur || !st.empty())
        {
            //1先访问左树节点
            while(cur)
            {
                st.push(cur);
                v.push_back(cur->val);
                cur = cur->left;
            }
            //这里左树为空了
            cur = st.top();
            st.pop();
            //以子问题的方式访问右树
            cur = cur->right;
        }
      return v;

    }
};

94. 二叉树的中序遍历 - 力扣（LeetCode）

这一题复制上一题的模板，就是在将要访问右树的时候在push_back;

145. 二叉树的后序遍历 - 力扣（LeetCode）

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        TreeNode* cur = root;
        stack<TreeNode*> st;
        TreeNode* prev = nullptr;
        vector<int> v;
        while(cur || !st.empty())
        {
            //1先访问左树节点
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            //cur是指要取访问的节点
            //top取出来判断后决定cur的指向
            TreeNode* top = st.top();
            if(top->right==nullptr || top->right == prev)
            {
                //这时候不用访问
                prev = top;
                v.push_back(top->val);
                st.pop();
                
            }
            else
            {
                cur =top->right;
            }
        }
      return v;
    }
};