1、概率统计知识

强化学习数学基础详解与示例
参考：https://blog.csdn.net/CltCj/article/details/119445005

1.1 随机变量与观测值

定义
随机变量是描述随机事件结果的变量，其取值具有不确定性；观测值则是随机事件实际发生后记录的具体结果。
示例：
假设抛一枚硬币，定义随机变量 $X$ 表示抛硬币结果：正面记为 $X=1$，反面记为 $X=0$。抛硬币前，$X$ 的取值是未知的，但概率分布已知（$P(X=1)=0.5$，$P(X=0)=0.5$）。若连续抛4次硬币，得到观测值序列 $x_1=1,x_2=0,x_3=1,x_4=1$，这些具体数值即为观测值。

---

1.2 概率密度函数（PDF）

定义
概率密度函数描述随机变量在某一取值附近的相对可能性。
• 连续型分布：如高斯分布 $\mathcal{N}(\mu ,{\sigma }^2)$，其概率密度函数为：
$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
该函数表明随机变量在均值 $\mu$ 附近取值的概率较高。
• 离散型分布：例如随机变量 $X$ 的取值为 {1, 3, 7}，对应的概率密度函数为：
$$P(X=1)=0.2,P(X=3)=0.5,P(X=7)=0.3$$
所有可能取值的概率之和为1。

---

1.3 期望

定义
期望是随机变量所有可能取值的概率加权平均，反映其长期平均结果。
• 连续型期望：
$$\mathbb{E}[f(X)]={\int }_{-\infty }^{\infty }f(x)p(x)dx$$
例如，高斯分布 $X\sim \mathcal{N}(0,1)$ 的期望为 $\mu =0$ 。
• 离散型期望：
$$\mathbb{E}[f(X)]=\sum _{x\in \mathcal{X}}f(x)P(X=x)$$
以离散分布 $P(X=1)=0.2,P(X=3)=0.5,P(X=7)=0.3$ 为例，其期望为：
$$\mathbb{E}[X]=1\times 0.2+3\times 0.5+7\times 0.3=3.8$$
。

---

1.4 随机抽样

定义
随机抽样是从概率分布中生成观测值的过程，用于近似理论分布。
示例：
假设一个箱子中有红球（20%）、绿球（50%）、蓝球（30%），每次随机抽取一个球并记录颜色。重复多次后，观测值的分布会趋近理论概率。通过Python代码实现：

import numpy as np
samples = np.random.choice(['R', 'G', 'B'], size=100, p=[0.2, 0.5, 0.3])

结果可能为 ['G', 'B', 'R', 'G', ...]，其中红球占比接近20%，绿球50%，蓝球30%。

---

强化学习中的关联应用

1. 策略函数中的动作选择：策略 $\pi (a|s)$ 可视为动作空间的概率密度函数，例如在状态 $s$ 下，动作 $a_1$ 的概率为0.7，$a_2$ 为0.3，通过随机抽样决定实际动作。
2. 状态转移的随机性：环境的状态转移概率 $P(s^{\prime }|s,a)$ 类似条件概率密度函数，例如智能体执行动作后，环境可能以80%概率转移到状态 $s_1$，20%概率到 $s_2$ 。
3. 蒙特卡洛方法：通过随机抽样轨迹估计状态价值函数，例如多次模拟游戏过程，计算平均回报以近似期望值。

2、数据期望E

https://zhuanlan.zhihu.com/p/481760712
离散型随机变量的一切可能的取值与对应的概率乘积之和称为该离散型随机变量的数学期望 [2]（若该求和绝对收敛），记为E（x）

3、正态分布

https://baike.baidu.com/item/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/829892
正态分布（Normal distribution），又称为常态分布或高斯分布，通常记作X~N（μ ,σ2）。其中， μ是正态分布的数学期望（均值）， σ2是正态分布的方差。μ = 0,σ = 1的正态分布被称为标准正态分布 [1]。

4、条件概率

https://baike.baidu.com/item/%E6%9D%A1%E4%BB%B6%E6%A6%82%E7%8E%87/4475278

• 条件概率
  条件概率是指事件A在事件B发生的条件下发生的概率。条件概率表示为：P（A|B），读作“A在B发生的条件下发生的概率”。若只有两个事件A，B，那么，。
• 联合概率
  表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P(A∩B)。 [2]
• 边缘概率
  是某个事件发生的概率，而与其它事件无关。边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率）。这称为边缘化（marginalization）。A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。

条件概率，多条件Xn，与多个条件相关和只与上一个条件相关：
当事件序列 $X_1,X_2,\dots ,X_n$ 的条件概率依赖关系不同时，联合概率的计算方式也会不同。

1. 与多个条件相关（依赖所有前置条件）

• 定义：每个事件 $X_i$ 的条件概率依赖于之前所有事件 $X_1,X_2,\dots ,X_{i-1}$ 的发生。
• 链式法则：
联合概率可分解为一系列条件概率的乘积，公式为：
$$P(X_1,X_2,\dots ,X_n)=P(X_1)\cdot P(X_2|X_1)\cdot P(X_3|X_1,X_2)\cdot \cdots \cdot P(X_n|X_1,\dots ,X_{n-1})$$

• 概率计算：在这种情况下，计算事件 A 发生的概率 P(A|B,C,D) 可以用联合概率除以边缘概率的方法，即 P(A|B,C,D) = P(A,B,C,D)/P(B,C,D)，其中 P(B,C,D) > 0。联合概率 P(A,B,C,D) 表示事件 A、B、C、D 同时发生的概率，边缘概率 P(B,C,D) 表示事件 B、C、D 同时发生的概率。

2. 仅与上一个条件相关（马尔可夫性质）

• 定义：每个事件 $X_i$ 的条件概率仅依赖于前一个事件 $X_{i-1}$，即 $P(X_i|X_1,\dots ,X_{i-1})=P(X_i|X_{i-1})$。
• 简化形式：
联合概率可简化为：
$$P(X_1,X_2,\dots ,X_n)=P(X_1)\cdot P(X_2|X_1)\cdot P(X_3|X_2)\cdot \cdots \cdot P(X_n|X_{n-1})$$
这种形式常见于时序模型（如马尔可夫链），例如网页 6 提到的股票价格预测中，当前价格可能仅依赖前一时段的价格。

• 概率计算：在这种情况下，条件概率可以简化为 P(A|B)，而不必考虑更前面的条件。例如，在一个二阶马尔可夫链中，事件 A 发生的概率只与前两个事件有关，即 P(A|B,C)，但与更早的事件无关。不过，对于一阶马尔可夫链，就只考虑前一个事件，即 P(A|B)。

5、马尔可夫

https://zhuanlan.zhihu.com/p/489239366
https://zhuanlan.zhihu.com/p/448575579

1、马尔可夫链

俄国数学家 Andrey Andreyevich Markov 研究并提出一个用数学方法就能解释自然变化的一般规律模型，被命名为马尔科夫链（Markov Chain）。马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程，该过程要求具备“无记忆性 ”，即下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。

状态转移矩阵的稳定性：
状态转移矩阵有一个非常重要的特性，经过一定有限次数序列的转换，最终一定可以得到一个稳定的概率分布 ，且与初始状态概率分布无关。

马尔科夫链（Markov Chain）-随机餐厅
https://zhuanlan.zhihu.com/p/489239366

2、n 阶马尔可夫链

http://www.mselab.cn/media/files/B03.%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E6%A8%A1%E5%9E%8B.pdf
马尔科夫过程是指过程中的状态的转移依赖于之前的状态，当影响转移状态的数目是n时,这个过程被称为 n阶马尔科夫模型.

N-Gram最简单有效，所以应用的也最广泛。它基于独立输入假设：第n个词的出现只与前面N-1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。

应用：
让机器“听懂”人类的语言，两个马尔科夫模型就解决了：
声学模型：利用HMM建模（隐马尔可夫模型），HMM是指这一马尔可夫模型的内部状态外界不可见，外界只能看到各个时刻的输出值。对语音识别系统，输出值通常就是从各个帧计算而得的声学特征。
语言模型：N-Gram最简单有效，所以应用的也最广泛。它基于独立输入假设：第n个词的出现只与前面N-1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。

3、马尔可夫奖励过程/决策过程

https://www.cnblogs.com/jsfantasy/p/jsfantasy.html
https://blog.csdn.net/qq_33302004/article/details/115027798
马尔科夫过程又叫做马尔科夫链（Markov Chain）,它是一个无记忆的随机过程，可以用一个元组<S, P>表示。（上节回顾）。

马尔科夫奖励过程：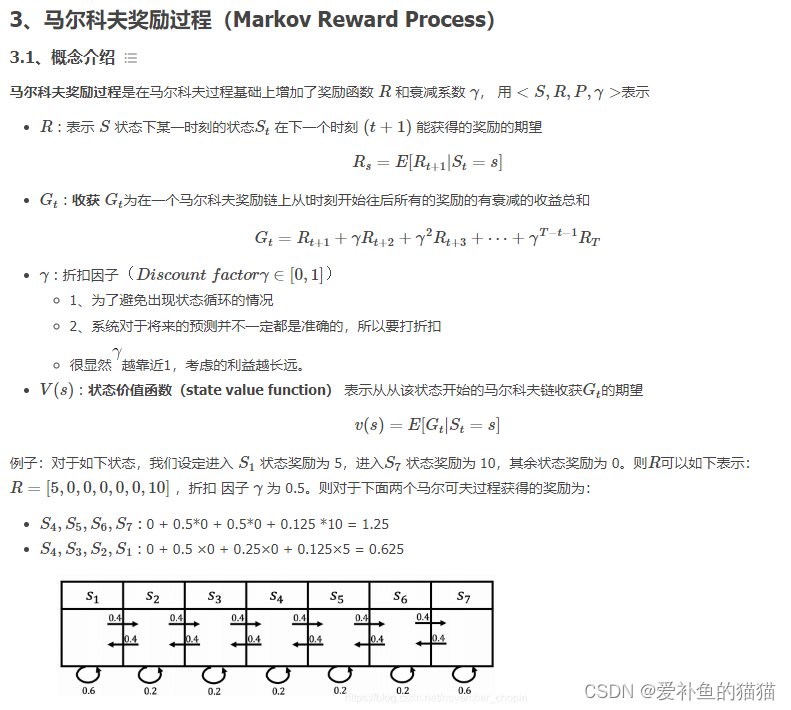
通过贝尔曼方程，可以看到价值函数有两部分组成，一个是当前获得的奖励的期望，另一个是下一时刻的状态期望，即下一时刻 可能的状态能获得奖励期望与对应状态转移概率乘积的和，最后在加上折扣。

马尔科夫决策过程（Markov Decision Process），马尔科夫决策过程是在马尔科夫奖励过程的基础上加了 Decision 过程，相当于多了一个动作集合。最优价值函数
解决强化学习问题意味着要寻找一个最优的策略让个体在与环境交互过程中获得始终比其它策略都要多的收获，这个最优策略我们可以用 π 表示。一旦找到这个最优策略π ，那么我们就解决了这个强化学习问题。一般来说，比较难去找到一个最优策略，但是可以通过比较若干不同策略的优劣来确定一个较好的策略，也就是局部最优解。

4、隐马尔可夫

https://zhuanlan.zhihu.com/p/35651762
https://zhuanlan.zhihu.com/p/151011287
https://zhuanlan.zhihu.com/p/547259609

隐马尔可夫模型（HMM）

隐马尔可夫模型（Hidden Markov Model，HMM）是一种统计模型，广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言应用领域。经过长期发展，尤其在语音识别中成功应用，使它成为一种通用的统计工具。

三个基本问题

https://blog.csdn.net/qq_52785580/article/details/135746941
https://zhuanlan.zhihu.com/p/151011287
https://zhuanlan.zhihu.com/p/88362664

前向算法、后向算法、Viterbi算法

https://zhuanlan.zhihu.com/p/35651762
https://zhuanlan.zhihu.com/p/547259609
https://zhuanlan.zhihu.com/p/29938926

6、KL散度(相对熵)

https://blog.csdn.net/Rocky6688/article/details/103470437
https://zhuanlan.zhihu.com/p/74075915
信息量、熵、相对熵（KL散度）、交叉熵、JS散度、推土机理论、Wasserstein距离、WGAN中对JS散度，KL散度和推土机距离的描述

1、相对熵（KL散度）

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。
在机器学习中，P往往用来表示样本的真实分布，Q用来表示模型所预测的分布，那么KL散度就可以计算两个分布的差异，也就是Loss损失值。
从KL散度公式中可以看到Q的分布越接近P（Q分布越拟合P），那么散度值越小，即损失值越小。
因为对数函数是凸函数，所以KL散度的值为非负数。
有时会将KL散度称为KL距离，但它并不满足距离的性质：
KL散度不是对称的；
KL散度不满足三角不等式。

2、交叉熵

7、贝尔曼方程

贝尔曼方程，又叫动态规划方程，是以Richard Bellman命名的，表示动态规划问题中相邻状态关系的方程。某些决策问题可以按照时间或空间分成多个阶段，每个阶段做出决策从而使整个过程取得效果最优的多阶段决策问题，可以用动态规划方法求解。某一阶段最优决策的问题，通过贝尔曼方程转化为下一阶段最优决策的子问题，从而初始状态的最优决策可以由终状态的最优决策(一般易解)问题逐步迭代求解。存在某种形式的贝尔曼方程，是动态规划方法能得到最优解的必要条件。绝大多数可以用最优控制理论解决的问题，都可以通过构造合适的贝尔曼方程来求解。

贝尔曼方程是强化学习中描述状态值函数（或动作值函数）递归关系的核心方程，其推导基于马尔科夫决策过程（MDP）和全期望公式。以下是关键步骤和逻辑：

---

1. 定义问题

• 状态值函数 $V^{\pi }(s)$：在策略 $\pi$ 下，从状态 $s$ 开始的期望累积回报：
  $$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\mid S_t=s\right]$$
  其中 $\gamma \in [0,1]$ 是折扣因子，$R_{t+k+1}$ 是未来奖励。
• 动作值函数 $Q^{\pi }(s,a)$：在状态 $s$ 执行动作 $a$ 后，遵循策略 $\pi$ 的期望累积回报：
  $$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\mid S_t=s,A_t=a\right]$$

---

2. 贝尔曼方程的推导

状态值函数的贝尔曼方程

1. 分解回报：将累积回报拆分为即时奖励和未来奖励：
   $$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma \sum _{k=1}^{\infty }{\gamma }^{k-1}{R}_{t+k+1}\mid S_t=s\right]$$
2. 利用马尔科夫性质：下一状态 $s^{\prime }$ 的转移概率仅依赖当前状态 $s$ 和动作 $a$，即 $P(s^{\prime }\mid s,a)$，且策略 $\pi (a\mid s)$ 决定动作选择。
3. 全期望公式展开：
   $$V^{\pi }(s)=\sum _a\pi (a\mid s)\left[R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }\mid s,a)V^{\pi }(s^{\prime })\right]$$
   其中 $R(s,a)=\mathbb{E}[R_{t+1}\mid S_t=s,A_t=a]$ 是即时奖励期望 。

动作值函数的贝尔曼方程

1. 类似地，对 $Q^{\pi }(s,a)$ 进行分解：
   $$Q^{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }\mid s,a)\sum _{a^{\prime }}\pi (a^{\prime }\mid s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })$$
   即当前动作 $a$ 的价值等于即时奖励加上未来动作价值的期望 。

---

3. 贝尔曼最优方程

若策略 $\pi$ 是最优策略 ${\pi }^{\ast }$，则值函数满足贝尔曼最优方程：
$$V^{\ast }(s)=\underset{a}{\max }\left[R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }\mid s,a)V^{\ast }(s^{\prime })\right]$$

$$Q^{\ast }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }\mid s,a)\underset{a^{\prime }}{\max }{Q}^{\ast }(s^{\prime },a^{\prime })$$
最优方程通过最大化未来价值，体现了“贪心”策略的选择 。

---

4. 关键思想

• 递归关系：当前状态的价值由即时奖励和未来状态的价值共同决定，形成递归结构 。
• 动态规划基础：贝尔曼方程是动态规划求解最优策略的核心，通过迭代更新值函数逼近最优解 。
• 折扣因子 $\gamma$：控制未来奖励的重要性，$\gamma =0$ 时仅关注即时奖励，$\gamma =1$ 时完全考虑长期回报 。

---

总结

贝尔曼方程通过将复杂的时间序列问题转化为递归形式，为强化学习提供了数学基础。其推导依赖于MDP的马尔科夫性、全期望公式和最优性原理 。

8、强化学习知识点

强化学习知识点链接