二叉树基础及实现（一）

目录：

一. 树的基本概念

二. 二叉树概念及特性

三. 二叉树的基本操作

一. 树的基本概念：

1 概念：

树是一种非线性的数据结构，它是由n（n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵 倒挂的树 ，也就是说它是 根朝上，而叶朝下 的。

特点：

（1）. 有一个特殊的结点（最上面的根，整个树的根），称为根结点，根结点没有前驱结点

（2）. 除根结点外，其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm，其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继

（3）. 树是递归定义的 。

注意：

（1）. 树形结构中，子树之间不能有交集，否则就不是树形结构

（2）.出了根节点外，每一个节点有且只有一个父节点

（3）. N个节点的树有（N-1）条条边。

结点的度 ： 一个结点含有子树的个数称为该结点的度；

树的度 ： 一棵树中，所有结点度的最大值称为树的度；

叶子结点或终端结点 ： 度为0的结点称为叶结点；

双亲结点或父结点 ： 若一个结点含有子结点，则这个结点称为其子结点的父结点；

孩子结点或子结点 ： 一个结点含有的子树的根结点称为该结点的子结点；

根结点 ： 一棵树中，没有双亲结点的结点；

结点的层次 ： 从根开始定义起，根为第1层，根的子结点为第2层，以此类推

树的高度或深度 ： 树中结点的最大层次

下面的了解即可：

非终端结点或分支结点 ： 度不为0的结点

兄弟结点 ： 具有相同父结点的结点互称为兄弟结点。

堂兄弟结点：双亲在同一层的结点互为堂兄弟

结点的祖先：从根到该结点所经分支上的所有结点。

子孙：以某结点为根的子树中任一结点都称为该结点的子孙。所有结点都是整个树的根节点的子孙

森林：由m（m>=0）棵互不相交的树组成的集合称为森林

2.树的应用

文件系统管理（目录和文件）

二. 二叉树概念及特性：

1. 概念：

一棵二叉树是结点的一个有限集合，该集合：

（1）或者为空

（2）或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

特点：

（1）二叉树 不存在度大于2的结点

（2）二叉树的 子树有左右之分，次序不能颠倒，因此二叉树是有序树

2 两种特殊的二叉树：

（1）满二叉树:

一棵二叉树，如果每层的结点数都达到最大值（就是每个节点度都等于2），则这棵二叉树就是满二叉树。

公式定义：也就是说，如果一棵二叉树的层数为K，且结点总数是(2^k - 1)(2的K次方减一)，则它就是满二叉树。

如图：

（2）完全二叉树:

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n 个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为 完全二叉树。

满二叉树是一种特殊的完全二叉树。

我的理解： （二叉树的节点从上到下从左到右按序号一次存放不间断）

图解：

3. 二叉树的性质 ：

(1). 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有（2的i次方减一）

(i>0)个结点

(2). 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是

(k>=0)

(3). 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1

（度为0的节点比度为2的节点多一个）：

推导如图：

(4). 具有n个结点的完全二叉树的深度k为，(log2 N+1，log2为底，N+1次方)上取整

(5). 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i 的结点有：

若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点

若2i+1<n，左孩子序号：2i+1，否则无左孩子

若2i+2<n，右孩子序号：2i+2，否则无右孩子

4 二叉树的存储:

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。

二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式 ，

具体如下：

// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}

孩子双亲表示法后序在平衡树位置介绍，本页博客采用孩子表示法来构建二叉树

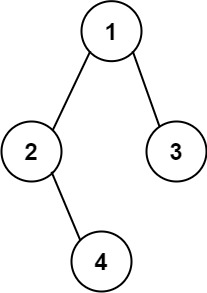
三. 二叉树的基本操作（与遍历相关）：

1.这里重点写一下二叉树的遍历方法：

前序遍历——访问根结点--->根的左子树--->根的右子树。

中序遍历——根的左子树--->根节点--->根的右子树。

后序遍历——根的左子树--->根的右子树--->根节点。

下面一些关于二叉树的方法的代码，主要是熟悉，递归和熟悉二叉树的遍历：

（1）前序遍历及前序子问题遍历：

图解：

// 前序遍历
    void preOrder(TreeNode root) {
        //结束条件
        if (root == null) {
            return;
        }

        //相当于递推公式：根 左树 右树
        System.out.print(root.val + " ");
        preOrder(root.left);
        preOrder(root.right);
    }


    //子问题思路前序遍历
    List preOrder2(TreeNode root) {
        //定义一个顺序表，每次递归，把递归的返回值放入顺序表
        List<Character> list = new ArrayList<>();
        //结束条件
        if (root == null) {
            return list;
        }

        list.add(root.val);

        List<Character> leftTree = preOrder2(root.left);
        list.addAll(leftTree);//返回时，把前一个左树放入顺序表中

        List<Character> rightTree = preOrder2(root.right);
        list.addAll(rightTree);//返回时，把前一个右树放入顺序表中

        return list;
    }

（2）后序中序遍历：

// 中序遍历
    void inOrder(TreeNode root) {

        //结束条件
        if (root == null) {
            return;
        }

        //相当于递推公式：左树 根 右树
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }

    // 后序遍历
    void postOrder(TreeNode root) {

        //结束条件
        if (root == null) {
            return;
        }

        //相当于递推公式： 右树 左树 根
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val + " ");
    }

（3）获得二叉树节点个数：

//遍历二叉树获得节点个数
    public static int nodeSize;
    public void size(TreeNode root) {
        if (root == null) {
            return;
        }

        nodeSize++;

        //递归遍历
        size(root.left);
        size(root.right);

    }


    //子问题思路二叉树获得节点个数
    //方法：左子树节点 + 右子树节点 + 1; '1'为概树第1个根节点
    public int size2(TreeNode root) {
        if (root == null) {
            return 0;
        }

        //树不为空，左子树节点 + 右子树节点 + 1
        return  size2(root.left) +
                size2(root.right) + 1;

    }

（4）获取叶子节点个数：

//获取叶子节点个数
    //遍历方法
    public static int NodeCount;
    public void getLeafNodeCount(TreeNode root) {
        if (root == null) {
            return;
        }

        //节点左右两节点都为null时，就是叶子结点
        if (root.left == null && root.right == null) {
            NodeCount++;
        }

        //有一边树不为空就递归遍历
        getLeafNodeCount(root.left);
        getLeafNodeCount(root.right);

    }


    //子问题方法
    public int getLeafNodeCount2(TreeNode root) {
        if (root == null) {
            return 0;
        }

        //节点左右两节点都为null时，就是叶子结点
        if (root.left == null && root.right == null) {
            return 1;
        }

        //方法:递归的方式，左叶子节点 + 右叶子节点
        /*
         这里递归时，满足叶子节点就会，return 上面的 1 给这个递归函数，最后返回叶子节点个数
         */
       return getLeafNodeCount2(root.left) +
               getLeafNodeCount2(root.right);
    }

（5）二叉树的高度：

图解：

//求第K层节点树
    /** 子问题方法：左边第k-1节点，加右边第K-1结点；
     *            因为二叉树每遍历一层就会，往下走一层，就是k的值就 减一
     *             当k1==1时就到了第K层
     */

    public int getKLeveNodeCount(TreeNode root, int k) {
        if (root == null) {
            return 0;
        }

        //返回条件是，k == 1就到了第K层；返回节点数
        if (k == 1) {
            return 1;
        }


        return getKLeveNodeCount(root.left, k-1) +
                getKLeveNodeCount(root.right, k-1);
    }

（6）找到指定的val 树：

图解：

public TreeNode findVal(TreeNode root, char val) {
        if (root == null) {
            return null;
        }

        //返回的条件是，找到val树。

        //根遍历
        if (root.val == val) {
            return root;
        }

        //遍历左树,找val
        TreeNode leftT = findVal(root.left, val);
        if (leftT != null) {
            return leftT;
        }

        //遍历右树,找val
        TreeNode rightT = findVal(root.right, val);
        if (rightT != null) {
            return rightT;
        }

        return null;
    }

还有两个：设计层序和判断一棵树是不是完全二叉树的方法，请听下回分解