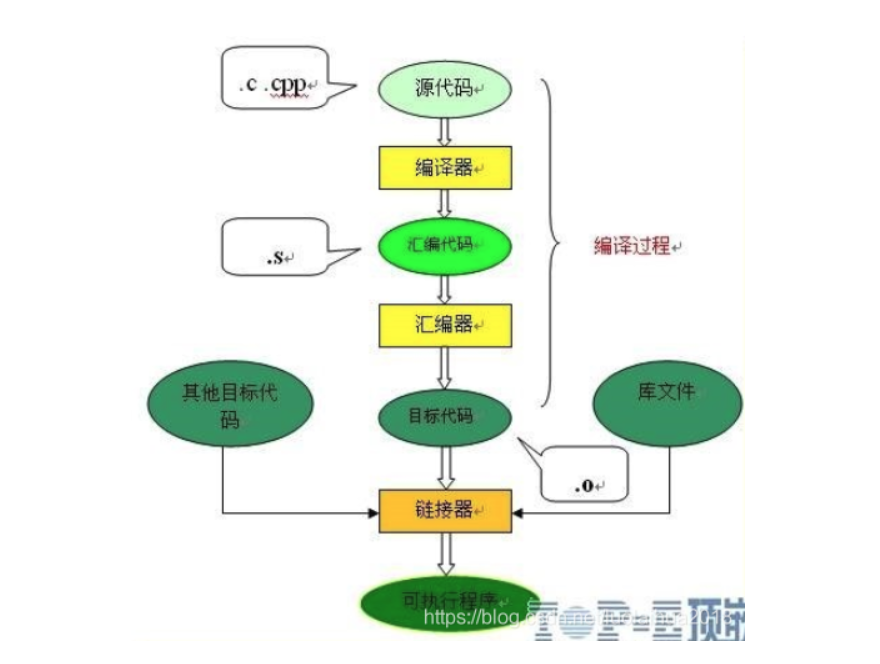
次为笔记记录，原视频链接为B站视频链接，若有错误请指出，看到就会改正

进制

r进制数及其转换成十进制数

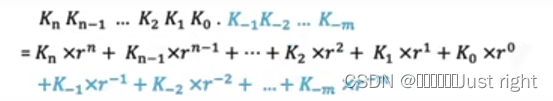
在这里插入图片描述
r^n就是第n位的维权,n<0就是小数部分的位权。
例子:1011
为十进制的时候:1011=1×10³+0×10²+1×10¹+1×10⁰
为二进制的时候
1011=1×2³+0×2²+1×2¹+1×2⁰=(10)10
为八进制的时候
1×8³+0×8²+1×8¹+1×8⁰=(521)10
为十六进制的时候
1×16³+0×16²+1×16¹+1×16⁰=(2990)10

十进制转换成r进制

对于整数部分就是除基取余数法.注意：到着取
对于小数部分是乘基取整法.注意：顺着取

例子

将十进制的32.125分别转换为二,八,十六进制
在这里插入图片描述

二,八,十六进制的转换

看例子: 二进制转换为八进制，三位一组，转换为十六进制，四位一组，整数部分不足的在前面补零，小数部分不足的在后面补零

B->O,H

二进制的101101011.1011
转换为八进制
101 101 011.101 100=553.6
转换为十六进制
1 0110 1011.1011=16B.B

BCD码

8421码

这个要掌握加法运算
四位二进制数能表示的状态是16种,但8421码只用前10种.

加法运算：出现非法码(10~15之间的),在非法码的基础上加上0110,低位向高位产生了进位，在低位加上0110.
每四位分成一组，在产生进位的组中加上0110

例子

用8421BCD码来计算9+9的结果
1001
+1001
10010
将10010+0110=1 1000 转换为十进制为18
0110

余3码

在8421码的基础上，每四位加0011即可

2421码

举个例子来说，求98的2421码
9=2+4+2+1
8=2+4+2
(98)2421=1111 1110

字符串

英文的就是ASCII码,需要注意的是A的ASCII码是65，a的ASCII是97，0是48
汉字的表示是用GB 2312-80来表示的
字符串的结束标志常采用’\0’作为结尾标志

大端模式与小端模式

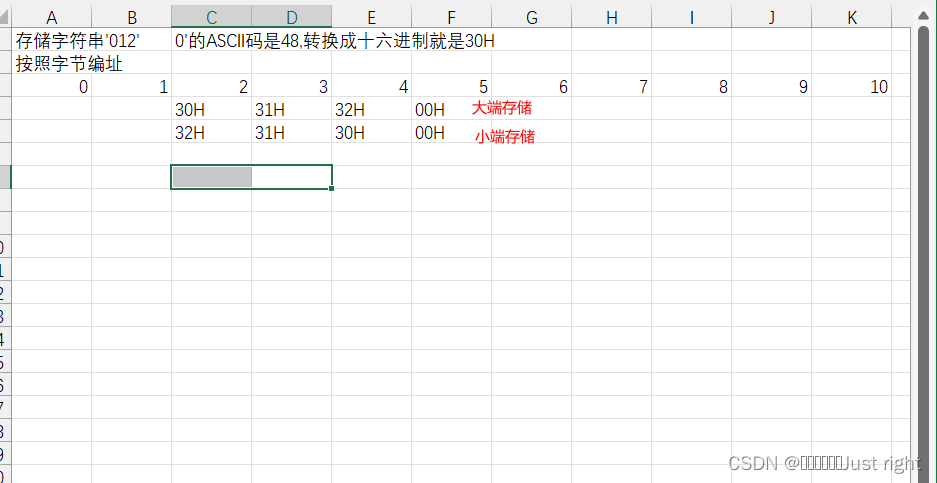
大端模式:将数据的最高有效字节存储在低地址单元中，这个模式便于人识别
小端模式:将数据的最高有效字节存储在高地址单元中.这个模式便于计算机识别
在这里插入图片描述

区位码,国标码,机内码的互相转换

区位码了解下,就是94个区,每个区94个位置,每个位置存放一个汉字,这样汉字就能数值化了,每个位置有一个唯一的编号,这样就能将汉字与数值对应起来

注:以下说明的+20H,+80H都是每两位加一个,不足两位前面补零凑齐两位
区位码+20H->国标码。个人理解,记公式也可以(之所以加20H是为了跳过控制/通信字符的)
国标码+80H->汉字内码个人理解,记公式也可以(之所以加80H是为了和英文做个区分,80H转换乘十进制就是128,英文的ASCII码是占用一个字节，最高位都是0,加上80H就是将每一个字节的最高位置为1)
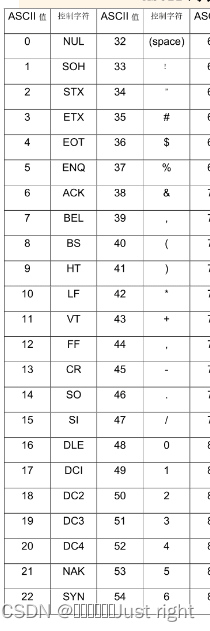
在这里插入图片描述

奇偶校验码

这个的纠错能力:1位,检错能力:2位

码字: 由若干位代码组成的一个字叫做码字
将两个码字逐位进行对比，具有不同的位的个数称为两个码字间的距离
合法码字间的最小距离称为’码距’

码距=1时，没有检错能力，等于2时有检错能力，大于等于3时，设计合理，可能具有检错、纠错能力

奇校验码:整个编码或者数据中的1的个数必须为奇数可以通过同或来实现
偶校验码:整个编码或者数据中的1的个数必须为偶数可以通过异或来实现

例子

1001 0001 0001的奇校验码为1 1001 0001 0001(1001 0001 0001中1的个数为偶数，所以校验位必须为1，才能保证1的个数为奇数)
偶校验码为0 1001 0001 0001(1001 0001 0001中1的个数为偶数，所以校验位必须为0，才能保证1的个数为偶数)

海明校验码

信息位:n
校验位:k
2^k>=n+k+1
找到满足条件的最小k
看一个例子
信息位:1011
信息位为4,带入2^k>=n+k+1得，k=3
校验位Pi需要放在海明码得2^i-1的位置上

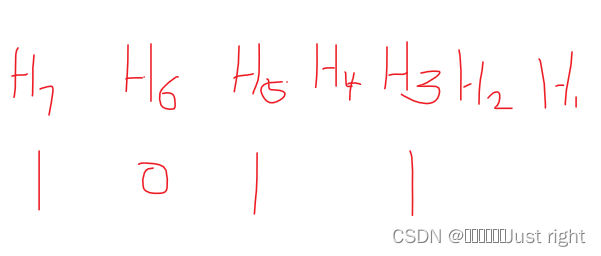
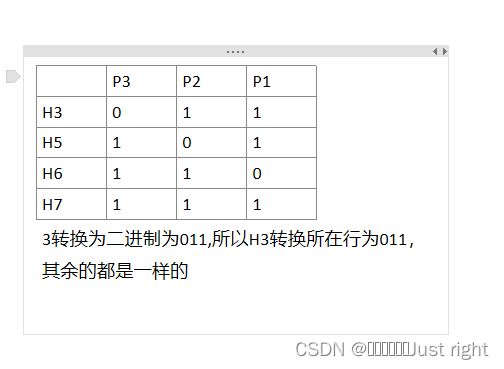
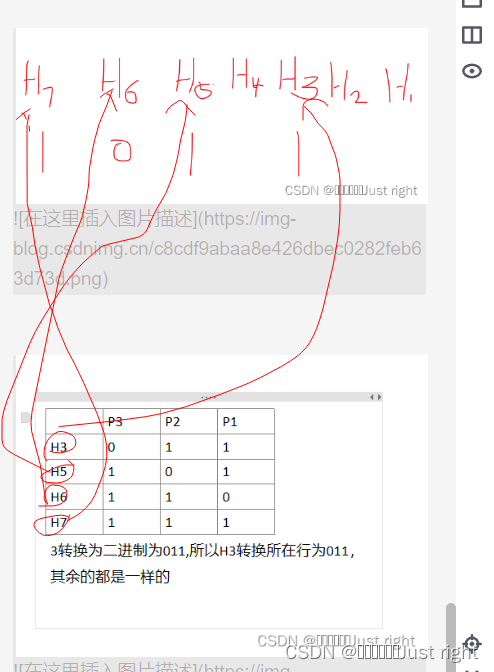
在这里插入图片描述

P1 = H3异或H5异或H7，就是只管P1所在列为1的部分，H3=1,H5=1,H7=1,P1的结果为1
P2 = H3异或H6异或H7=1异或0异或1=0
P3=H5异或H6异或H7=1异或0异或1=0
所以最终结果为1010101
校验方程
在这里插入图片描述
如果元数据为1010101，接收到的数据时1010001

P1=1(就是最后一位.因为2^i-1=1.i此时等于1),H的下标是从最后一位开始的，比如H1就是最后一位(从左往右数)
S1 = 1异或1异或1异或1=0
S2 = 0异或1异或0异或1=0
S3= 0异或1异或0异或1 = 1
S3 S2 S1 = 100 转换为二进制为4，就是从右往左数，第四位出错了，将第四位取反即可

最后

加上一个全校验位进行偶校验
若S3 S2 S1 =000且全体偶校验成功就是无错误
若S3 S2 S1 ≠000且全体偶校验失败就是有1位错误，取反
若S3 S2 S1 ≠000且全体偶校验成功就是有2位错误，需要重传

循环冗余校验码 CRC

这个用于网络传输比较多一点，几千个bit+几个校验位
我个人理解就是约定一个除数，将接收到的信息对除数进行模2除,如果除数等于0就是没有错误，反之就有错误，但是这个余数的所代表的位置不一定就是错误的.

k个信息位，r个校验位，满足2^r>=k+r+1，crc码可纠正1位错误

例子:生成的多项式G(x)=x³+x²+1,信息码位101001，求对应的CRC码。
生成的多项式为 1101（G(X)=x³+x²+x⁰,如果式子中有该位的序号就是1，如有3，那么第四位就是1，有0，那么第一位就是1，如果没有就是0)，G（x)最大幂数是3，需要将101001逻辑左移3位得到101001000.
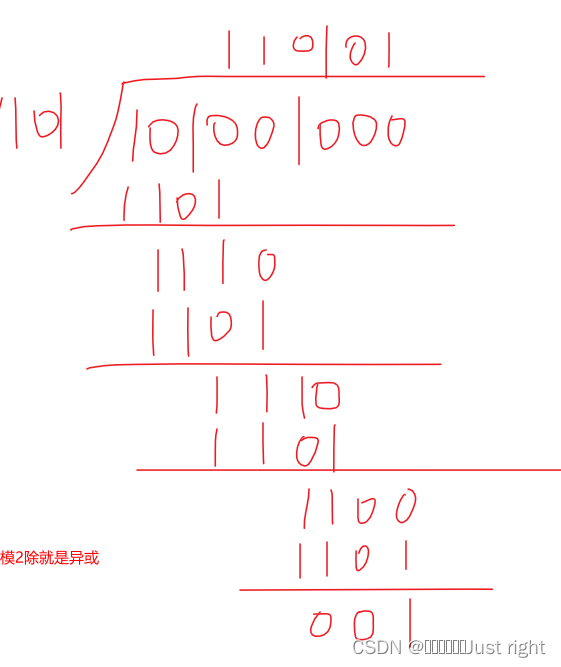
在这里插入图片描述
最终结果位101001001

定点数的表示

无符号数

没有符号位，全部都是数值位,相当于数的绝对值
范围:n位的无符号数的表示范围0~2ⁿ-1

有符号数

原,反,补,移码

原码:若为负数，符号位为1，若为正数符号位为0.
反码:正数的原,反,补码都是一样的，负数的反码就是符号位不变,各位取反
补码:负数的补码在反码的基础上面+1
移码:在补码的基础上将符号位取反即可。

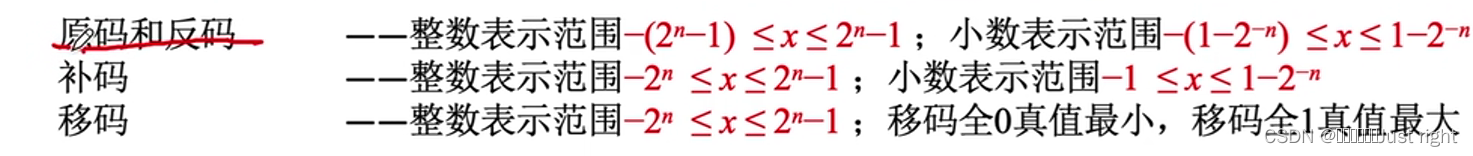
移码主要是方便比较大小

运算

[x+y]补=[x]补+[y]补
[x-y]补=[x]补+[-y]补
判断溢出:
单符号位:
在这里插入图片描述

双符号位:当符号位为01时则上溢,当符号位为10则位下溢

移位运算

算数移位

符号位保持不变,仅仅对数值位进行移位。所有的正数的算数移位都与原码一样
原码右移高位补零，低位丢弃，原码左移低位补零，高位丢弃
反码:负数右移高位补1，低位丢弃,反码左移低位补1,高位丢弃
补码:负数右移高位补1,低位丢弃,反码左移低位补0,高位丢弃
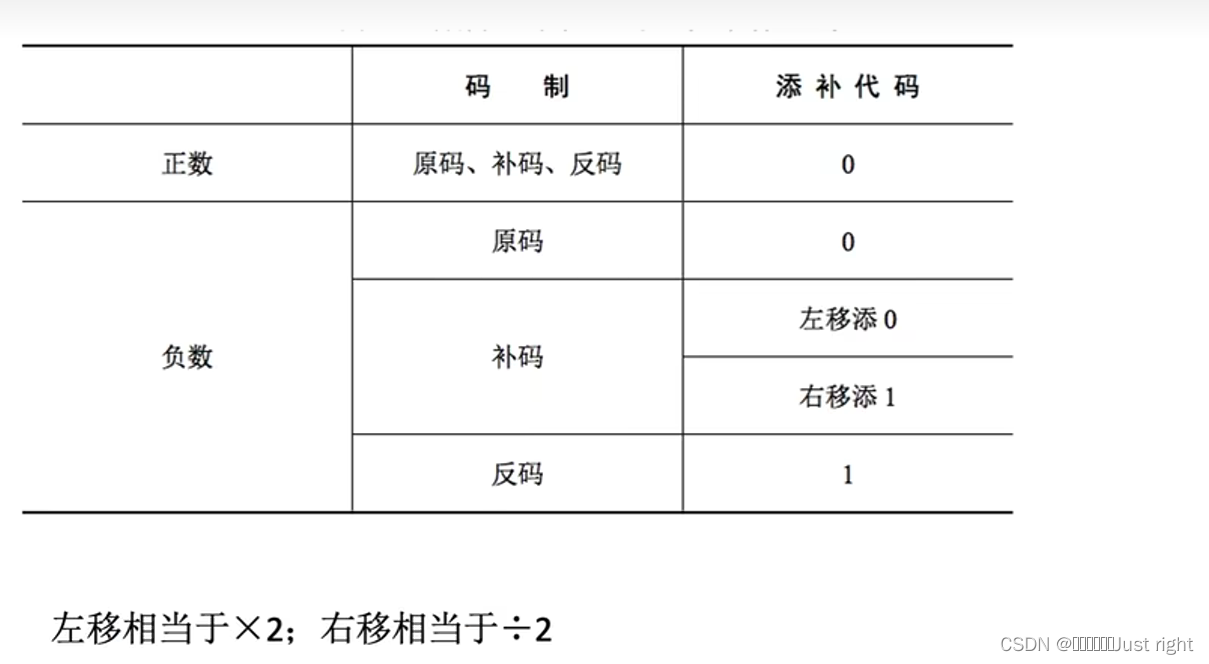
在这里插入图片描述
应用

逻辑移位

逻辑右移:高位补0,低位舍弃
逻辑左移:低位补0,高位舍弃

循环移位

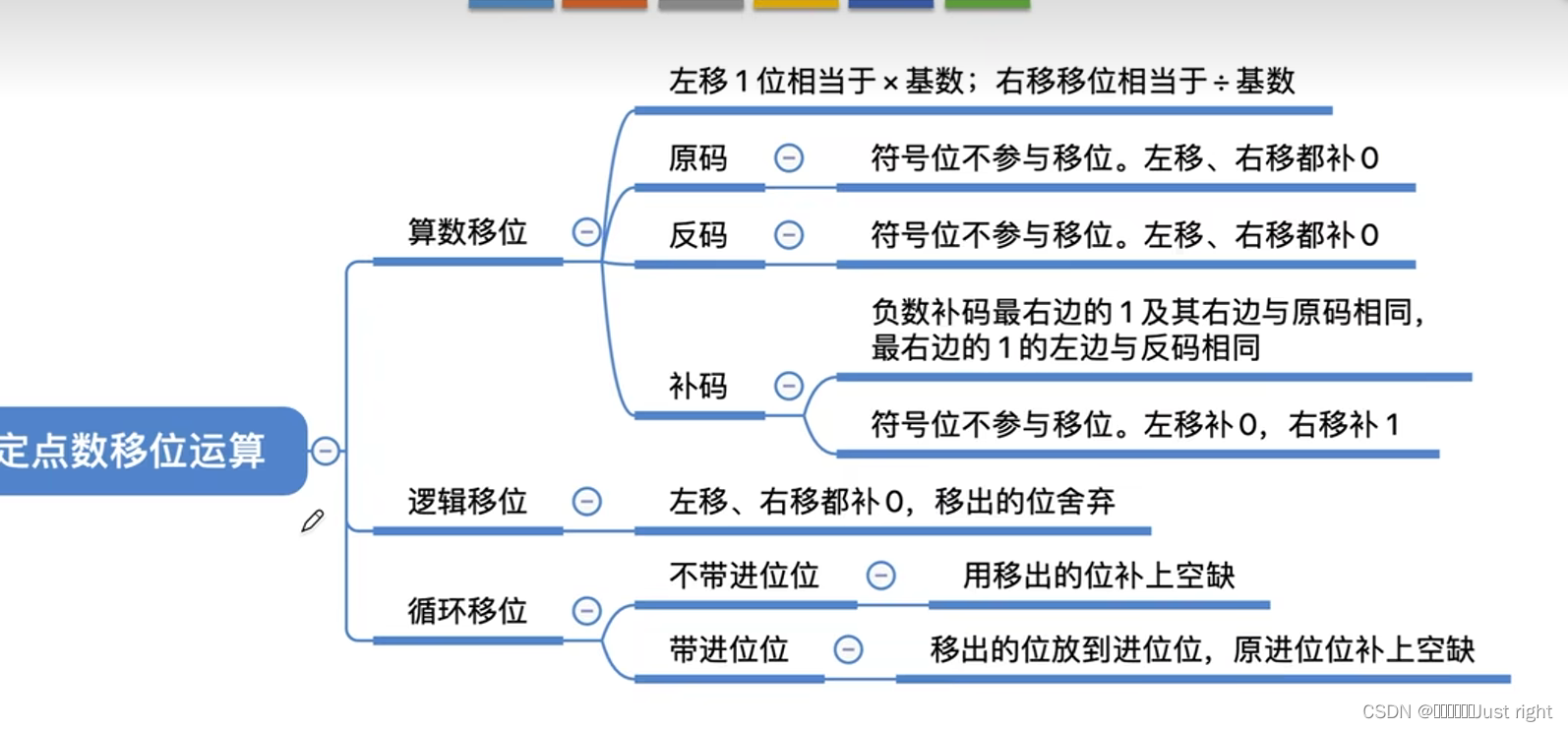
在这里插入图片描述

符号扩展

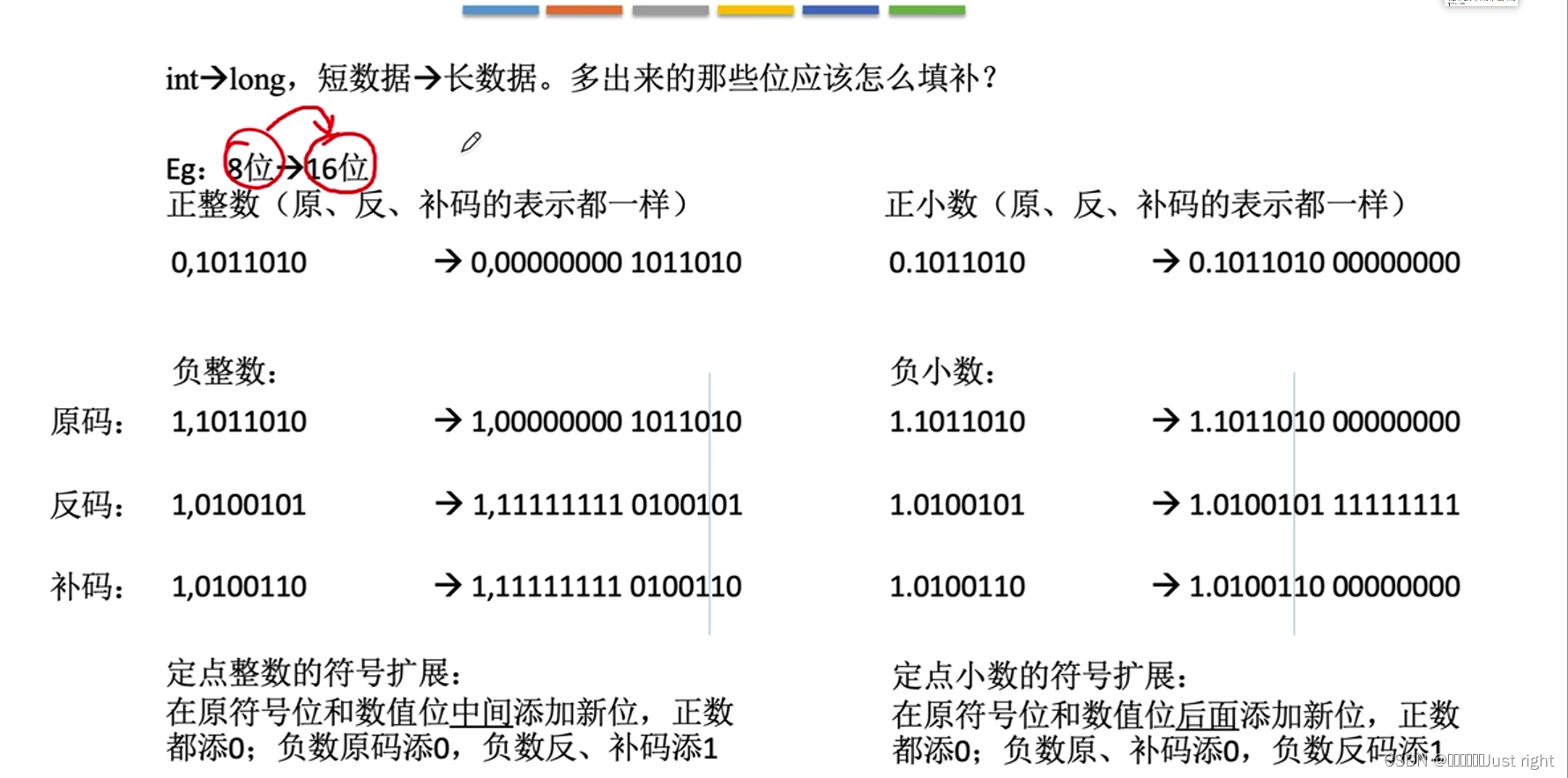
在原符号位和数值位中间添加新位,正数都添0,负数原码添0,负数反,补码添1

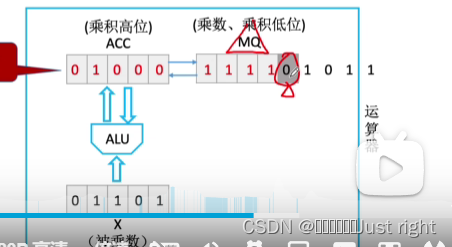
原码的乘法运算

将MQ的最后一位与X相乘存储到ACC中，再进行逻辑右移，重复，知道MQ的乘数被移除
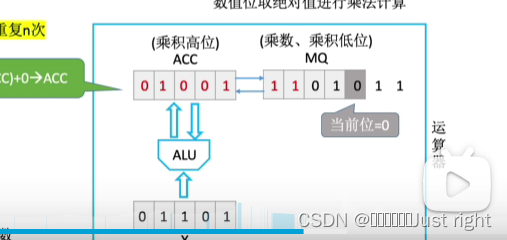
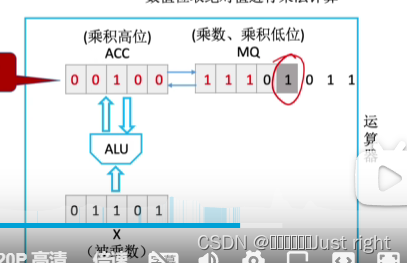
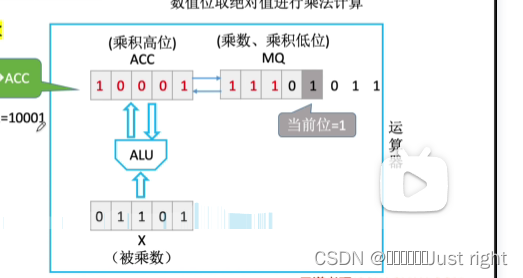
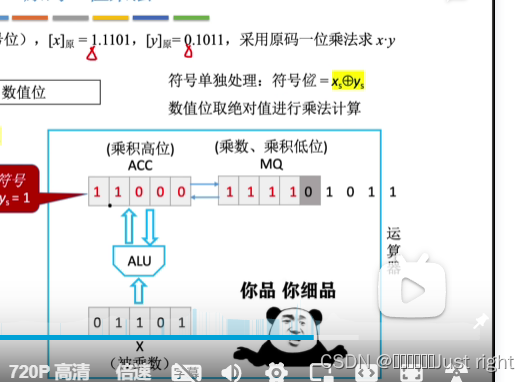
在这里插入图片描述

在这里插入图片描述

补码一位乘法

Booth算法
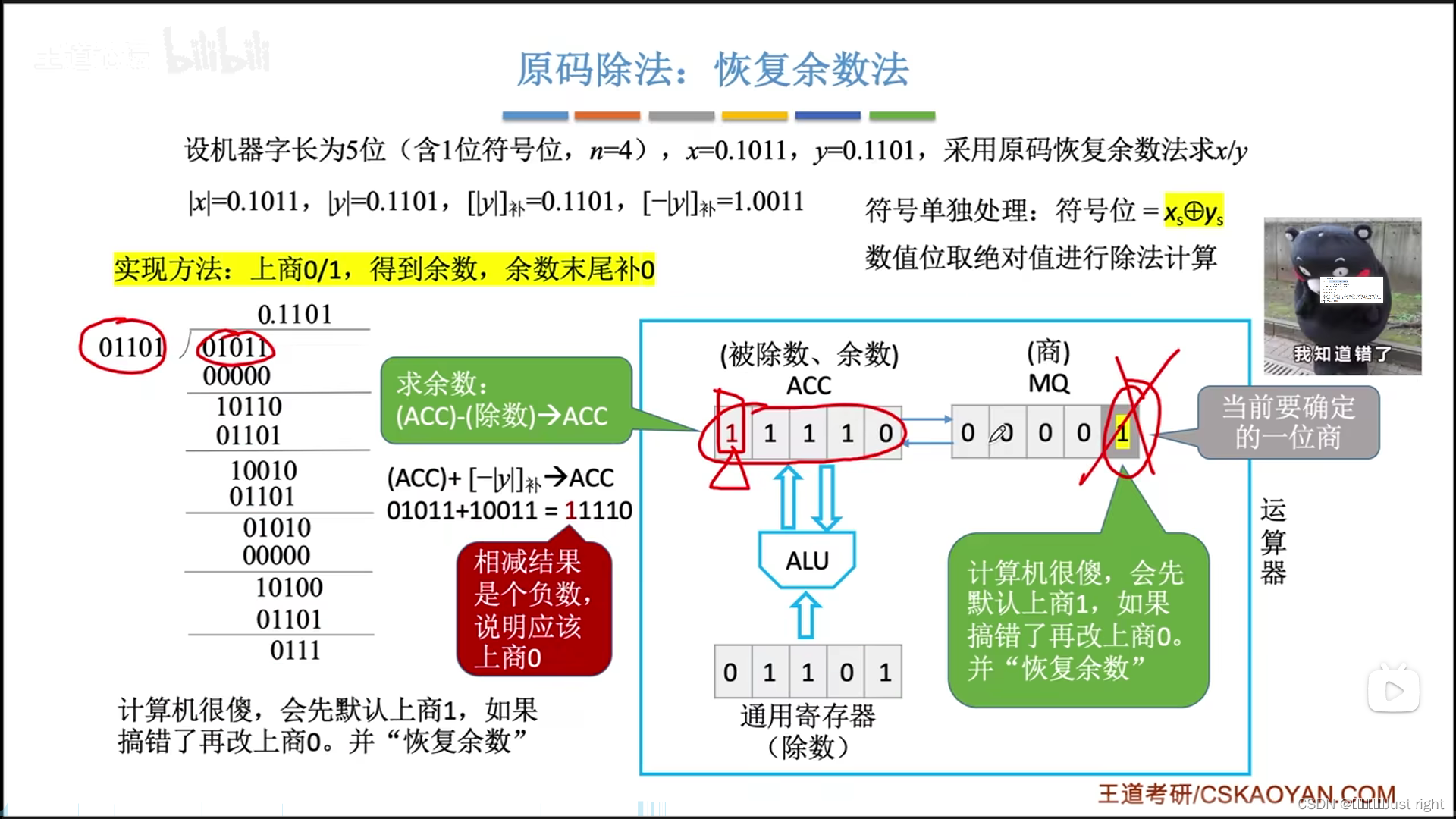
在这里插入图片描述

原码除法

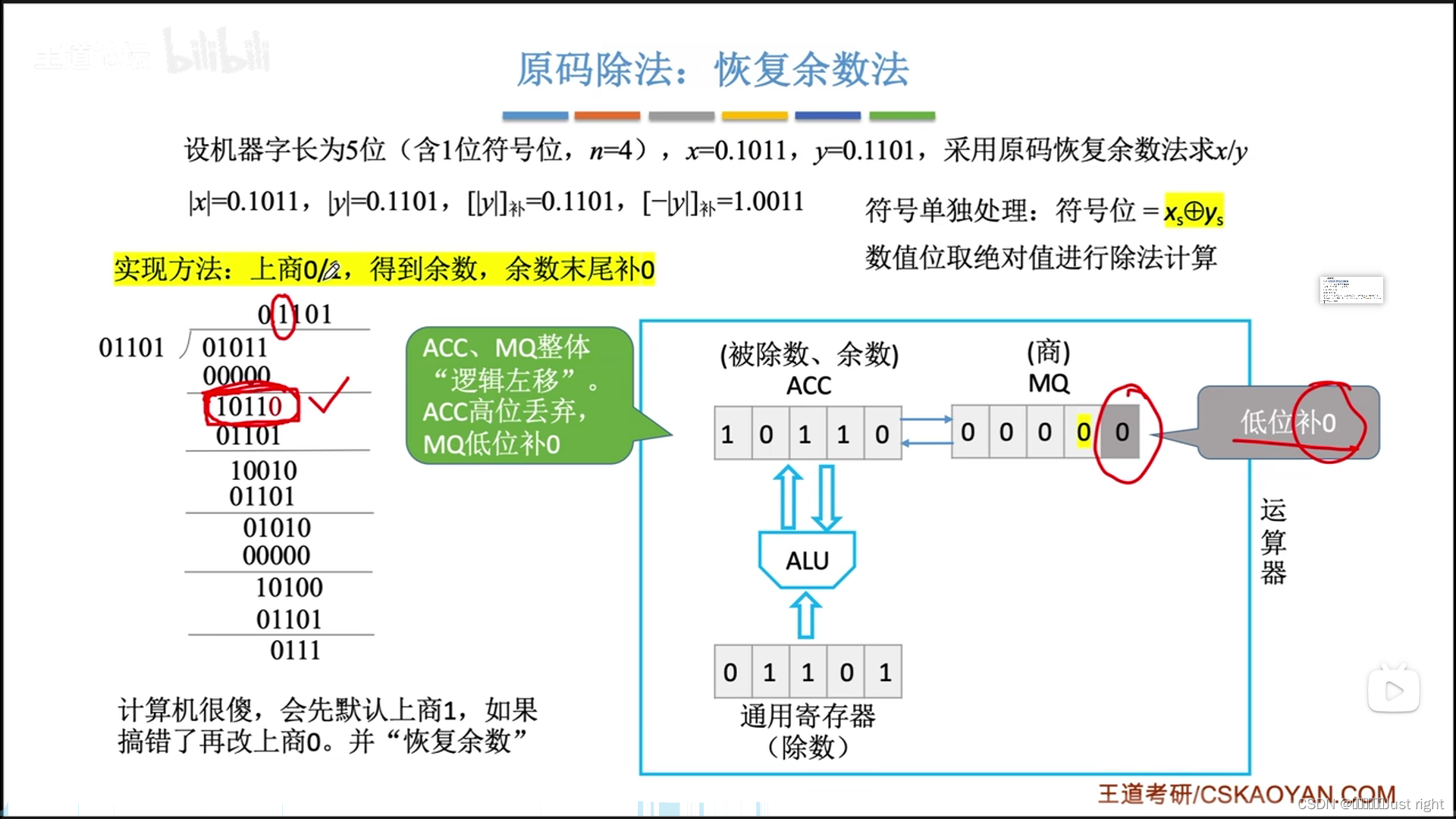
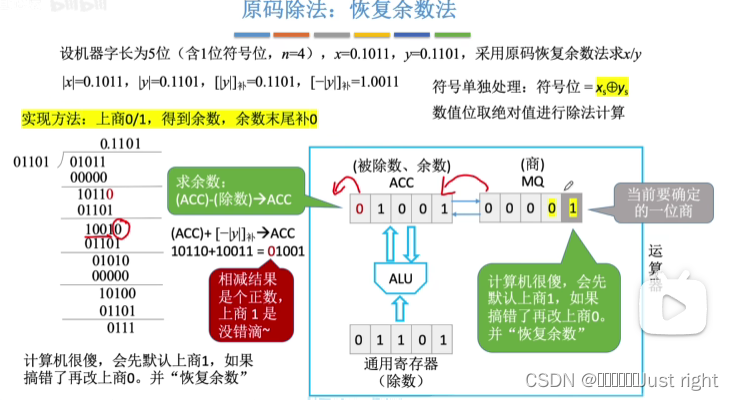
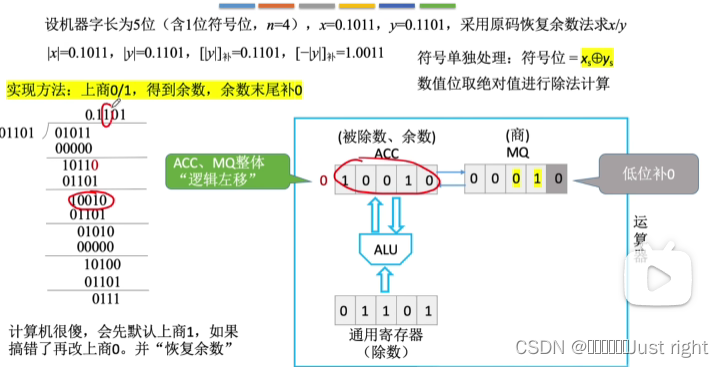
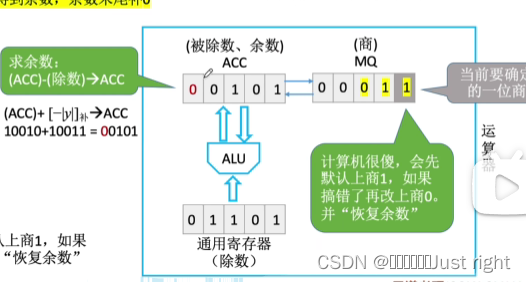
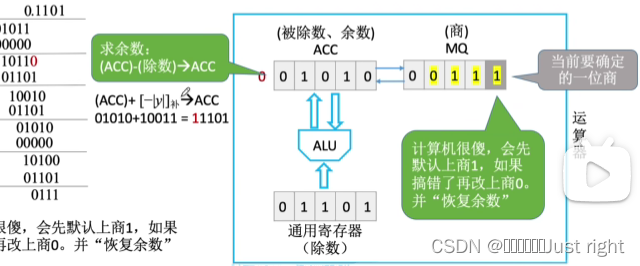
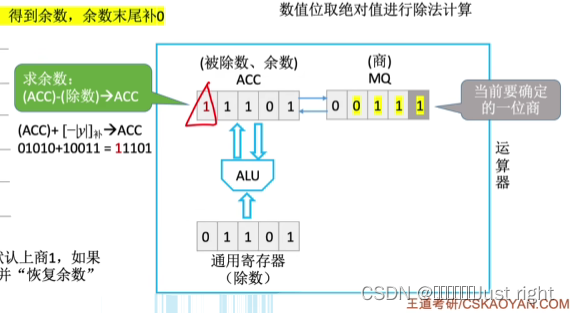
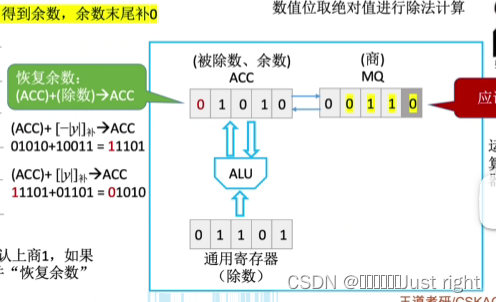
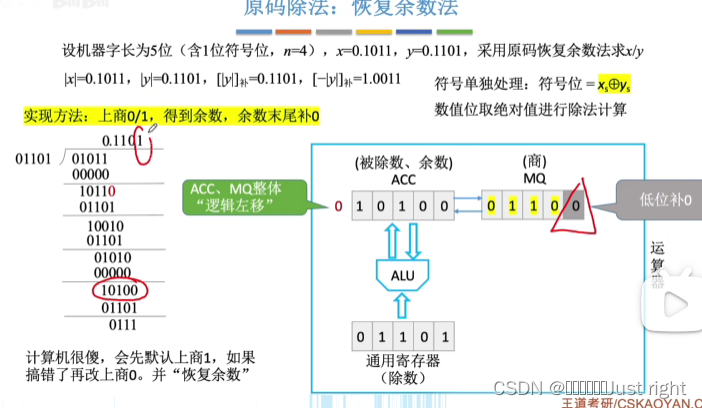
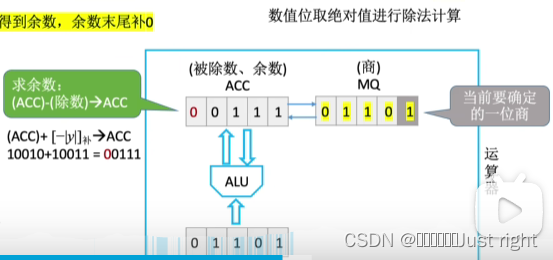
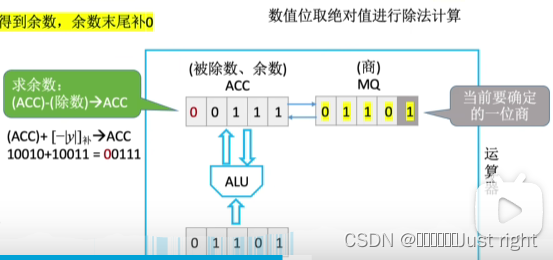
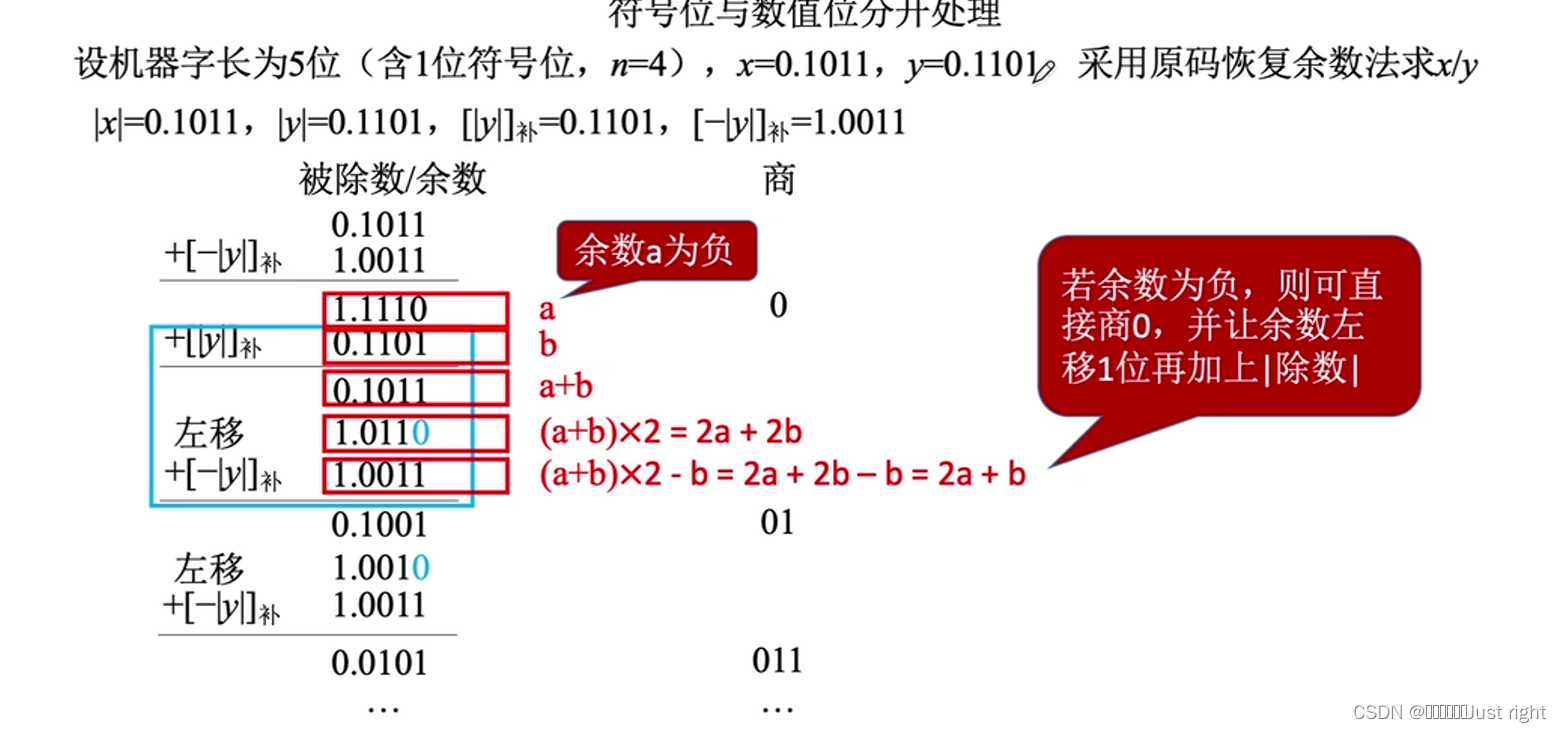
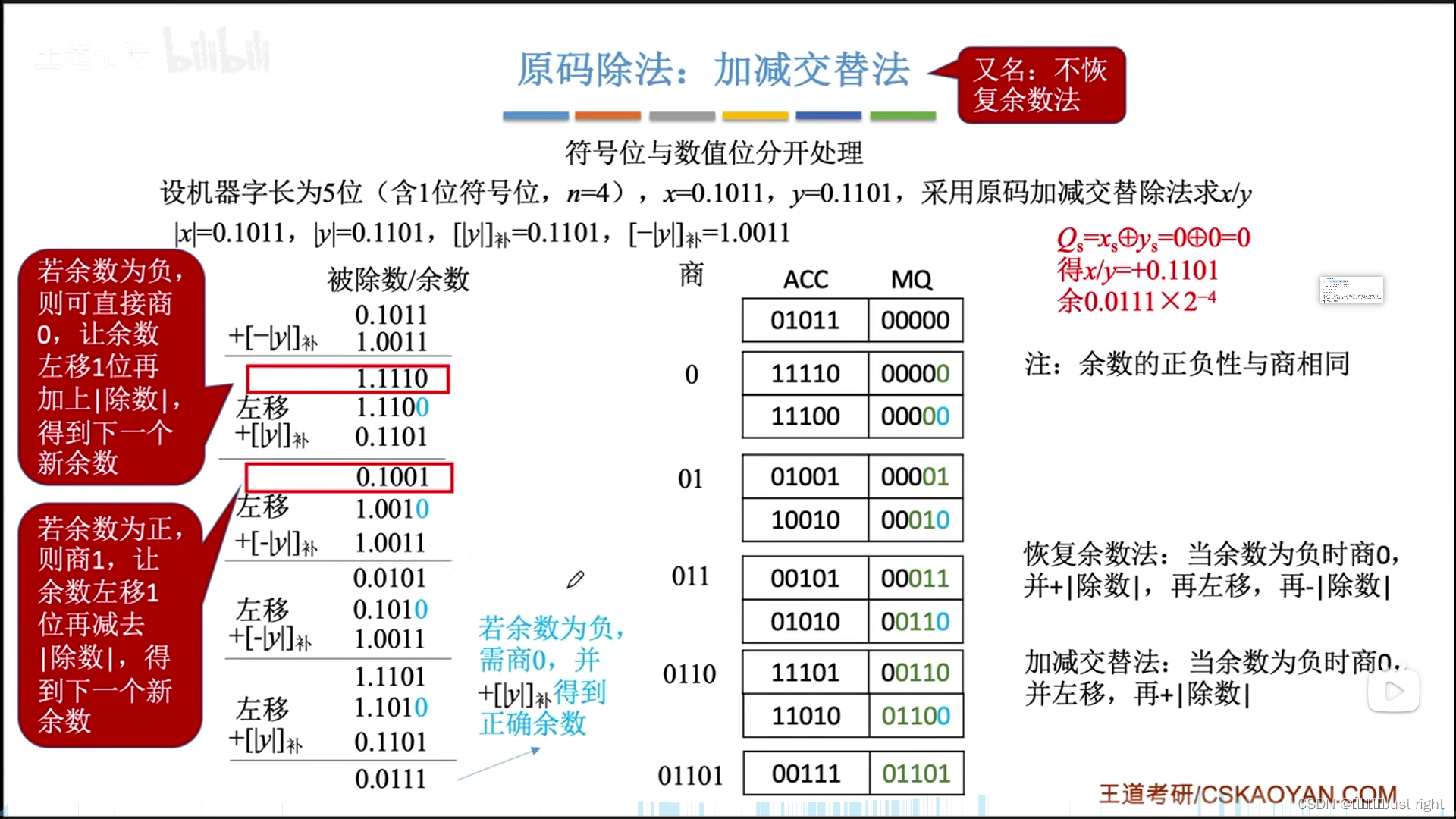
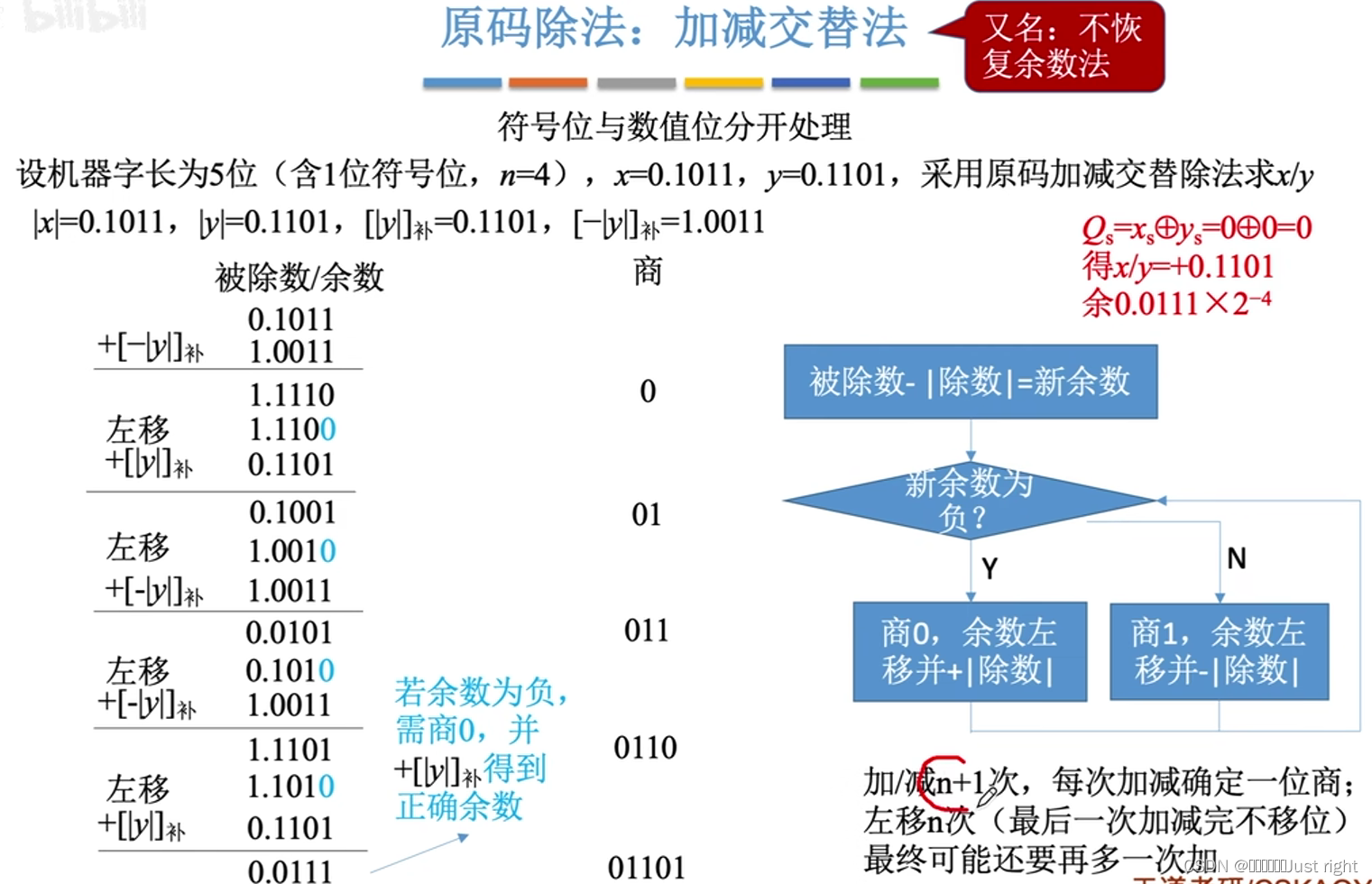
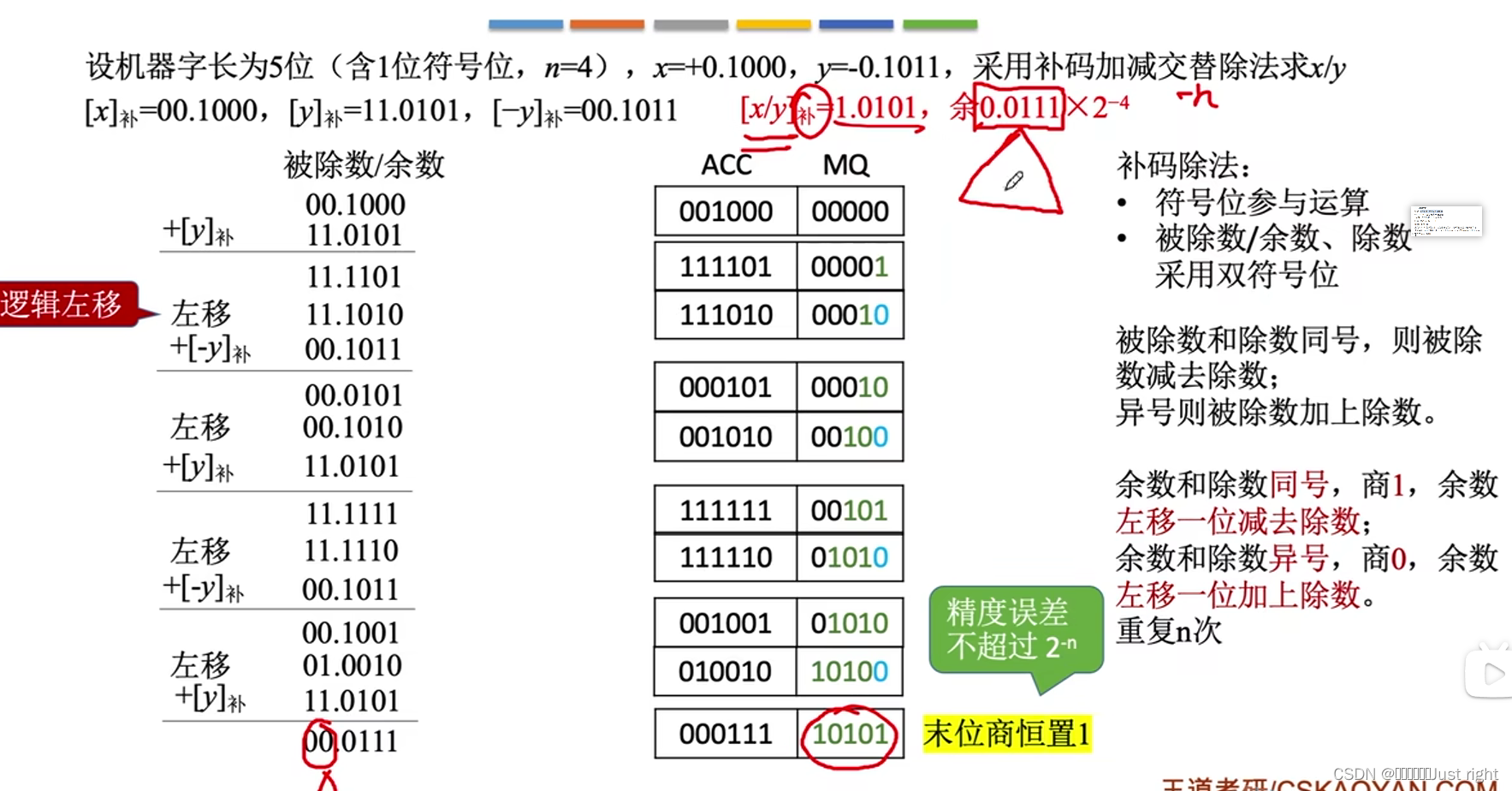
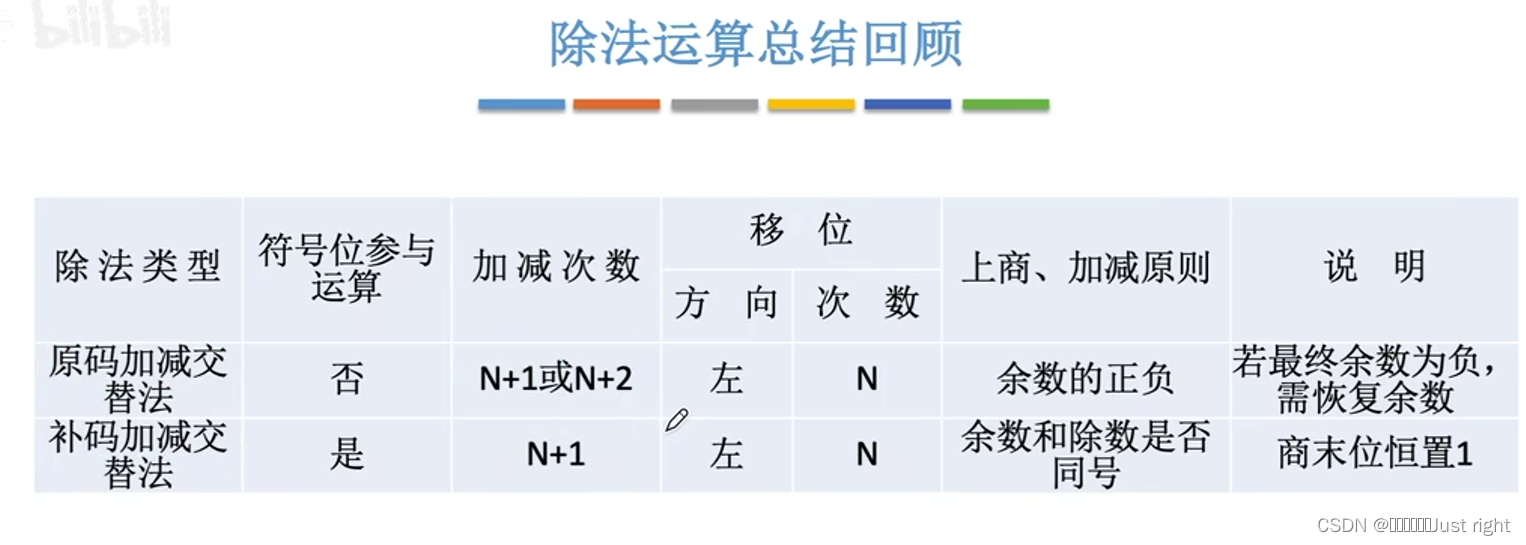
在这里插入图片描述

补码除法

在这里插入图片描述

强制类型转换

int a=165537,b=34991;
short c=(short)a,d=(short)b;
在这里插入图片描述
short x=-4321;
int m=x;
x: 1110 1111 0001 1111
m:1111 1111 1111 1111 1110 1111 0001 1111
是以补码存储的，x是负数，负数符号位扩展添加1(在符号位与数值之间)

浮点数

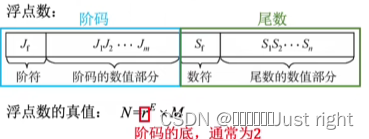
在这里插入图片描述
阶码E反映浮点数的表示范围及小数点的实际位置,常用补码或移码表示的定点整数
尾数M的数值部分的位数n反映浮点数的精度,常用原码或补码表示的定点小数
阶码.尾数都用补码表示，求a，b的真值
a=0,01;1.1001
b=0,10;0.01001
a=2¹×(-0.0111)=-0.111
b=2²×(0.01001)=1.001

规格化

左规:尾数算数左移一位,阶码减一
右规:尾数算数右移一位,阶码加一(双符号位为01或10时)
在这里插入图片描述

若某浮点数的阶码，尾数用补码表示，共4+8位，0.110;1.1110100如何规格化
2 ⁶×(-0.0001100)
2³×(-0.1100)

IEEE 754标准

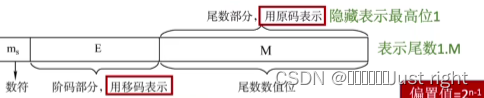
在这里插入图片描述
规格化的短浮点数的真值为(-1)^s×1.M×2^E-127

将十进制数-0.75转换为IEEE 754的单精度浮点数格式表示
(-0.75)10=(-0.11)2=(-1.1)×2^-1
数符:1位,因为是负数所以为1
阶码:8位 -1 + 111 1111=0111 1110 凑足8位
尾数:23位 10000000000000000000000
结果: 1 0111 1110 10000000000000000000000

IEEE 753的单精度浮点数 C0 A0 00 00H的值是多少
1 100 0000 1010 0000 0000 0000 0000 0000
数符:为1 所以是负数
阶码:8位 1000 0001看成无符号数 129D
尾数:23位 010 0000 0000 0000 0000 0000
2^129-127×(-1.01)=2²×(-1.01)=-101=-5
特点

当阶码E全为0,尾数M不全为0时,表示非规格化小数
例如:2⁰×1.00000001111
当阶码E全为0,尾数M全为0时,表示真值正负0
例如:2⁰×(-1.00000000000)=-0
2⁰×(1.00000000000)=0
当阶码E全为1,尾数M全为0时,表示无穷大(正负都有)
当阶码E全为1,尾数M不全为0时,表示非数值

运算

这里我可能算错了，你们选择的看
例题:
已知十进制数X=-5/256,Y=59/1024，按照及其补码浮点数运算规则计算X-Y,结果用二进制表示,浮点数格式如下:阶符取2位,阶码取3位,数符取2位,尾数取9位，用补码表示阶码和尾数
X=-101×2^-8=-0.101×2^-3=-0.101×2^-011,Y=-111011×2^-10=-0.111011×2^-4=-0.111011×2^-100
x: 11 011 11 0110 00000
y: 11 100 00 0111 01100

对阶: 小的向大的对齐（绝对值小的向大的对齐
求阶差:[▲E]补=11011+ 00 100=11 111=-1 x<y
对阶: x:11 011 11 10110 0000 (补码算数右移，空出来的补1)
尾数相减
-Y = 11 100 11 000101000
X-Y=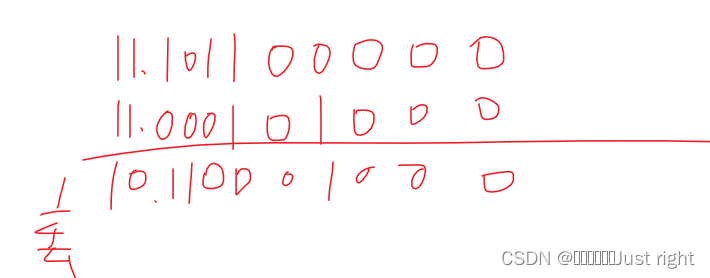
规格化
X-Y= 11 100 10.1100 0100 0=11 101 11.011000100
双符号位算数右移 10.1100 0100 0 ->10.011000100->11.011000100
舍入: 没有舍入
舍入方法1:0舍1入.最后一位是1就进1，若是0直接舍去
方法2:恒置1 最后一位恒置1
判溢出:无溢出