求和路径00

news2025/7/8 18:18:15

题目链接

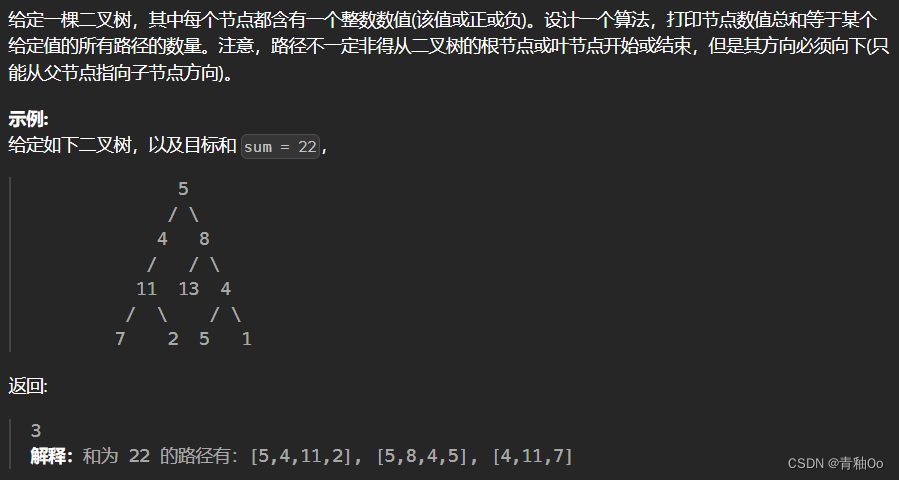
求和路径

题目描述

注意点

节点总数 <= 10000
节点的值可能是正数或负数
路径不一定非得从二叉树的根节点或叶节点开始或结束，但是其方向必须向下(只能从父节点指向子节点方向)

解答思路

因为要求树的路径和，所以初始想到的是深度优先遍历，如果暴力求每条路径的路径和，那么很多路径会重复计算，所以考虑使用前缀和
使用map存储前缀和，其中key是前缀和，value是前缀和为preSum的数量，前缀和是从根节点到达任意一个节点的路径和（未到达根节点则前缀和为0，方便后续讨论从根节点出发的路径和）
当到达任意一个节点node，此时从根节点root到达node的路径和为curr，以node作为路径末尾时路径和为sum的路径数量应该是map.getOrDefault(curr - sum, 0)，解释为curr是root到node的路径和，curr - sum是root到node的某个父节点parent的路径和，此时parent的下一个节点与node之间的路径和就是sum，满足题意（具体有没有这个parent取决于map.get(curr - sum)是否为0
当到达任意一个节点node，还要更新前缀和对应的map，也就是将curr + node.val存进map中，方便继续深搜遍历，在深搜完成后，要对前缀和进行回溯，否则node的同一层或者父节点进行深搜时会出错

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int res = 0;
    public int pathSum(TreeNode root, int sum) {
        Map<Integer, Integer> map = new HashMap<>();
        // 前缀和为0也就是从根节点出发的路径和
        map.put(0, 1);
        dfs(root, sum, 0, map);
        return res;
    }

    public void dfs(TreeNode node, int sum, int curr, Map<Integer, Integer> map) {
        if (node == null) {
            return;
        }
        curr += node.val;
        res += map.getOrDefault(curr - sum, 0);
        // 记录前缀和
        map.put(curr, map.getOrDefault(curr, 0) + 1);
        dfs(node.left, sum, curr, map);
        dfs(node.right, sum, curr, map);
        // 该节点的情况已讨论完，前缀和回溯
        map.put(curr, map.get(curr) - 1);
    }
}