1. 背

首先，考虑没有环的情况。如果没有环这道题可以转变为和打家劫舍II一毛一样。但是明明这道题是三块披萨一拿啊，打家劫舍是相邻不能拿，还是不一样啊。

这块证明挺难的，但是我可以用个简单的例子。例如008080，这种情况我能拿到16的披萨，因为我把第一个0拿走后，就变成了0空空空80，此时我再拿8，aclice可以拿前面那个0，也是能办到的。

反正最终的结果就是只要两个不相邻就行。

dp[i][j]表示前i个数字中，选择j个数字时的最大值。dp的行就是slice数组的长度，即元素的个数。dp的列就是行除以3（即能拿几次披萨）。不过，不过哈，写代码不能这么定义行列的长度，后面再说。
因此dp[i][j] = max(dp[i-2][j-1]+slices[i],dp[i-1][j])，如果选择第i个元素，那么i-1就不能选，就得选i-2，如果不选i，必须选好j个数字，因此就是dp[i-1][j]。

那么有环怎么办，还和打家劫舍II一样，判断[0,n-2]和[1,n-1]。问题又来了，传入的明明时3的倍数，我手动删掉一个，还能是3的倍数吗？不是的话肯定有影响，但是因为影响的是其他人的结果，但是题目只问我能拿多少披萨。

最后一个问题，上面说了dp数组的横纵长度不能直接用数组长度啥的表示，答案是这样的，它们把横纵坐标长度都加了一，原因很简答，保证数组从1开始。注意dp的定义“前i个数字中，选择j个数字时的最大值”，前0个数字不好处理，所以变成前1个数字。

2. 题目

给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

你挑选 任意 一块披萨。
Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/pizza-with-3n-slices
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

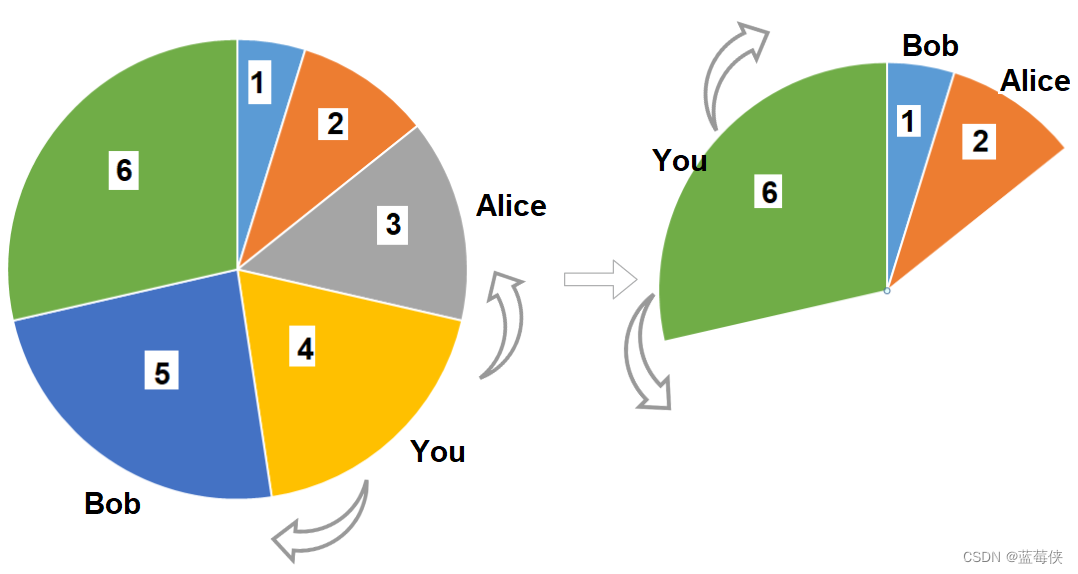
输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/pizza-with-3n-slices
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

3. 答案

class Solution {
public:
    int maxSizeSlice(vector<int>&slices)
    {
        int row = static_cast<int>(slices.size());
        int col = (row+1)/3;
        vector<vector<int>>dp(row+1,vector<int>(col+1,0));
        for(int i=1;i<=row;++i)
        {
            for(int j=1;j<=col;++j)
            {
                auto num1 = (i-2>=0&&j-1>=0?dp[i-2][j-1]:0)+slices[i-1];
                auto num2 = i-1>=0?dp[i-1][j]:0;
                dp[i][j] = max(num1,num2);
            }
        }
        return dp[row][col];
    }
    int maxSizeSlices(vector<int>& slices) {
        vector<int>a1(slices.begin(),slices.end()-1);
        vector<int>a2(slices.begin()+1,slices.end());
        auto num1 = maxSizeSlice(a1);
        auto num2 = maxSizeSlice(a2);
        return max(num1,num2); 
    }
};