四则运算Java版

数据结构之栈的应用之四则运算_文丑颜不良啊的博客-CSDN博客

之前有写过一篇关于栈的应用之四则运算的文章，是用 C++ 写的，涉及到一些指针的操作，同时，那篇文章有一个致命的错误，就是只支持 10 以内的混合运算，两位数的运算并不支持，所以，为了完善上篇文章的缺点，今天写一篇 Java 版本的四则运算。基本逻辑与 C++ 版相同。

比如，现在有一个混合表达式为：800 / { 5 * [ ( 34 + 46 ) / 8 ] }，根据运算规则可得，该表达式的结果为 2。对于计算机而言，需要把中缀表达式转换为后缀表达式之后再进行运算，即将中缀表达式 800 / { 5 * [ ( 34 + 46 ) / 8 ] } 转换为后缀表达式为：800 5 34 46 + 8 / * /

其转换过程一般遵循如下规则：

从左到右先遍历中缀表达式的每个数字和符号
若是数字就直接输出，即成为后缀表达式的一部分；
若是左括号，则直接入栈；
若是运算符号，则判断其与栈顶符号的优先级，若是栈顶元素的优先级大于等于当前运算符的优先级，则栈顶元素依次出栈并输出，并将当前运算符号进栈；（即如果当前运算符是加减，只要栈顶符号不是左括号，则全部出栈并输出，再将加减入栈；若当前运算符为乘除，栈顶元素若是乘除，则将乘除出栈并输出，再将乘除入栈，其余情况下将乘除直接入栈）
若是右括号，则需要与左括号进行匹配，所以栈中元素依次输出，直到左括号输出。

所以，对于中缀表达式 800 / { 5 * [ ( 34 + 46 ) / 8 ] } 来说，使用栈 operatorStack 来存储运算符和括号，使用 tempOperandBuffer 作为操作数的缓冲区，方便处理多为操作数，使用 postfixExpressionArray[] 来临时记录后缀表达式。因为涉及到小括号、中括号和大括号，所以为了方便处理，统一把中括号和大括号替换为小括号，这样的话，大概就可分为三个步骤：

处理中括号和大括号；
中缀表达式转换为后缀表达式；
后缀表达式求值

中缀表达式转换为后缀表达式

对于中缀表达式转换为后缀表达式的步骤，有如下处理过程：

1. 初始化后缀表达式数组 postfixExpressionArray、运算符栈 operatorStack 和操作数缓冲区 tempOperandBuffer ；

2. 处理前 3 个字符，即 '8'、'0'、'0'，因为前 3 个字符都是数字，所以存储进操作数缓冲区 tempOperandBuffer 中，待 flag 标识为 true 时存储进后缀表达式数组中；

3. 处理第 4 个字符，即除号运算符 '/'，根据转换规则，需要判断当前运算符与栈顶元素的优先级，因为此时栈为空，所以直接将 '/' 入栈，同时更新 flag 标识，准备后续处理操作数缓冲区的内容；

4. 处理第 5 个字符，即括号 '('，因为是左括号，所以直接入栈即可；

5. 处理第 6 个字符，即操作数 '5'，根据转换规则，如果是操作数的话，可以直接根据 flag 标识判断是更新草组数缓冲区还是存储进后缀表达式数组中。因为第 5 个字符 '(' 处理完成后，已经更新 flag 为 true 了，所以此时将操作数缓冲区的内容 "800" 直接存储进后缀表达式数组中，同时更新操作数缓冲区为 "5" 和 flag 标识即可；

6. 处理第 7 个字符，即运算符乘号 '*'，根据转换规则，需要判断与栈顶元素的优先级，因为此时栈顶元素为左括号 '('，所以直接将当前运算符入栈并更新 flag 标识即可；

7. 处理第 8、9 个字符，因为是左括号 '('，所以直接入栈并更新 flag 标识即可；

8. 处理第 10 个字符，即操作数 '3'，根据转换规则，如果是操作数的话，可以直接根据 flag 标识判断是更新操作数缓冲区还是存储进后缀表达式数组中。因为第 9 个字符 '(' 处理完成后，已经更新 flag 为 true 了，所以此时将操作数缓冲区的内容 "5" 直接存储进后缀表达式数组中，同时更新操作数缓冲区为 "3" 和 flag 标识即可；

9. 处理第 11 个字符，即操作数 '4'，根据转换规则，如果是操作数的话，可以直接根据 flag 标识判断是更新操作数缓冲区还是存储进后缀表达式数组中。因为第 10 个字符 '3' 处理完成后，已经更新 flag 为 false 了，所以此时选择更新操作数缓冲区的内容为 "34" 并更新 flag 标识即可；

10. 处理第 12 个字符，即运算符加号 '+'，根据转换规则，需要判断与栈顶元素的优先级，因为此时栈顶元素为左括号 '('，所以直接将当前运算符入栈并更新 flag 标识即可；

11. 处理第 13、14 个字符，即操作数 '4' 和 '6'，根据转换规则，如果是操作数的话，可以直接根据 flag 标识判断是更新操作数缓冲区还是存储进后缀表达式数组中。因为第 12 个字符 '+' 处理完成后，已经更新 flag 为 true 了，所以此时将操作数缓冲区的内容 "34" 直接存储进后缀表达式数组中，同时更新操作数缓冲区为 "46" 和 flag 标识即可；

12. 处理第 15 个字符，即右括号 ')'，根据转换规则，需要匹配左括号 '('，即需要将栈中距离栈顶最近的 '(' 之前的运算符依次出栈，并且存储进后缀表达式数组中，需要注意的是将运算符存储后缀表达式数组之前需要先将操作数缓冲区中的内容（即 "46"）存储进后缀表达式数组中，并更新操作数缓冲区和 flag 标识，处理完成之后还需要将栈中的栈顶元素出栈，即将左括号 '(' 出栈，需要注意的是只需要出栈一个左括号即可，所以可以通过 break 实现。于是，处理完成此右括号之后为：

13. 处理第 16 个字符，即运算符除号 '/'，根据转换规则，需要判断与栈顶元素的优先级，因为此时栈顶元素为左括号 '('，所以直接将当前运算符入栈并更新 flag 标识即可；

14. 处理第 17 个字符，即操作数 '8'，根据转换规则，如果是操作数的话，可以直接根据 flag 标识判断是更新操作数缓冲区还是存储进后缀表达式数组中。因为第 16 个字符 '/' 处理完成后，已经更新 flag 为 true 了，所以此时选择将操作数缓冲区的内容存储进后缀表达式数组中，同时更新操作数缓冲区的内容为 "8" 并更新 flag 标识即可；

15. 处理第 18 个字符，即右括号 ')'，根据转换规则，需要匹配左括号 '('，即需要将栈中距离栈顶最近的 '(' 之前的运算符依次出栈，并且存储进后缀表达式数组中，需要注意的是将运算符存储后缀表达式数组之前需要先将操作数缓冲区中的内容（即 "8"）存储进后缀表达式数组中，并更新操作数缓冲区和 flag 标识，处理完成之后还需要将栈中的栈顶元素出栈，即将左括号 '(' 出栈，需要注意的是只需要出栈一个左括号即可，所以可以通过 break 实现。于是，处理完成此右括号之后为：

16. 处理第 19 个字符，即右括号 ')'，根据转换规则，需要匹配左括号 '('，即需要将栈中距离栈顶最近的 '(' 之前的运算符依次出栈，并且存储进后缀表达式数组中，需要注意的是将运算符存储后缀表达式数组之前需要先将操作数缓冲区中的内容存储进后缀表达式数组中，并更新操作数缓冲区和 flag 标识，处理完成之后还需要将栈中的栈顶元素出栈，即将左括号 '(' 出栈，需要注意的是只需要出栈一个左括号即可，所以可以通过 break 实现。于是，处理完成此右括号之后为：

17. 此时，中缀表达式遍历完成，需要处理栈中剩余元素和操作数缓冲区中的内容。先处理数据缓冲区中的内容，直接存储进后缀表达式数组中即可；然后将栈中剩余元素依次存储进后缀表达式数组中，则处理完成之后为：

因此，中缀表达式：800 / { 5 * [ ( 34 + 46 ) / 8 ] } 转换为后缀表达式为：800 5 34 46 + 8 / * /。

后缀表达式求值

规则：从左到右遍历后缀表达式中的每个数字和符号，遇到数字就进栈，遇到符号，就将处于栈顶的两个数字出栈，并进行运算，将运算结果入栈，直到获得最终结果，最终结果即为栈顶元素。使用 calculateStack 用来记录结果。

1. 初始化 calculateStack；

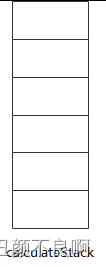
2. 处理前 4 个元素，根据规则，前 4 个元素都为操作数，即全部入栈；

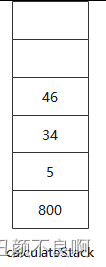
3. 处理第 5 个元素，即运算符 "+"，根据规则，需要使用栈中前两个元素进行计算，即 34 + 46 = 60，并将结果 60 入栈；

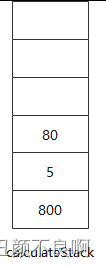
4. 处理第 6 个元素，即操作数 "8"，直接入栈即可；

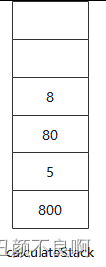
5. 处理第 7 个元素，即运算符 "/"，根据规则，需要使用栈中前两个元素进行计算，即 80 / 8 = 10，并将结果 10 入栈；

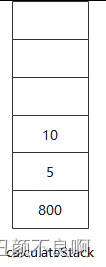
6. 处理第 8 个元素，即运算符 "*"，根据规则，需要使用栈中前两个元素进行计算，即 5 * 10 = 50，并将结果 50 入栈；

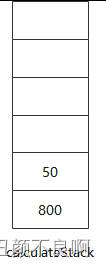
7. 处理第 9 个元素，即运算符 "/"，根据规则，需要使用栈中前两个元素进行计算，即 800 / 50 = 16，并将结果 16 入栈；

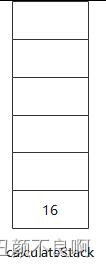
8. 后缀表达式处理完成，直接返回栈顶元素即为最终计算结果。

完整代码如下：

package mixingOperation;

import java.util.Stack;

public class MixingOperation {

    public static int mixingOperation(String infixExpression) {
        System.out.println("原始中缀表达式为: " + infixExpression);
        // 1. 处理中括号和小括号
        String newInfixExpression = handlerParentheses(infixExpression);
        System.out.println("处理括号后的新的中缀表达式为: " + newInfixExpression);
        // 2. 中缀表达式转换为后缀表达式
        String[] postfixExpressionArray = transformExpression(newInfixExpression);
        StringBuffer postfixExpressionBuffer = new StringBuffer();
        for (int i = 0; i < postfixExpressionArray.length; i++) {
            if (null == postfixExpressionArray[i] || postfixExpressionArray[i].isEmpty()) {
                break;
            }
            postfixExpressionBuffer.append(postfixExpressionArray[i]).append(" ");
        }
        System.out.println("后缀表达式为: " + postfixExpressionBuffer.toString());
        // 后缀表达式求值
        int result = calculateResultByPostfixExpression(postfixExpressionArray);
        System.out.println("表达式: " + infixExpression + " = " + result);
        return 0;
    }

    private static int calculateResultByPostfixExpression(String[] postfixExpressionArray) {
        // 运算符和运算数栈
        Stack<String> calculateStack = new Stack<>();
        // 遍历中缀表达式数组
        for (int i = 0; i < postfixExpressionArray.length; i++) {
            if (null == postfixExpressionArray[i] || postfixExpressionArray[i].isEmpty()) {
                break;
            }
            String currentStr = postfixExpressionArray[i];
            switch (currentStr) {
                // 如果是运算符, 将栈顶元素作为第二个操作数并出栈, 然后新的栈顶元素作为第一个操作数并出栈,
                // 然后使用 操作数1、运算符、操作数2 进行运算, 并将结果入栈
                case "+" :
                case "-" :
                case "*" :
                case "/" :
                    if (!calculateStack.empty()) {
                        // 栈顶元素作为操作数2并出栈
                        int operand2 = Integer.valueOf(calculateStack.pop());
                        // 新的栈顶元素作为操作数1
                        int operand1 = Integer.valueOf(calculateStack.pop());
                        // 计算结果
                        int result = calculateResult(operand1, currentStr, operand2);
                        // 将结果入栈
                        calculateStack.push(String.valueOf(result));
                    }
                    break;
                default:
                    // 如果是操作数, 则直接入栈
                    calculateStack.push(currentStr);
            }

        }
        // 处理完成之后输出栈顶元素即为最终结果
        return Integer.valueOf(calculateStack.pop());
    }

    private static int calculateResult(int operand1, String currentStr, int operand2) {
        int result = 0;
        switch (currentStr) {
            case "+" :
                result =  operand1 + operand2;
                break;
            case "-" :
                result =  operand1 - operand2;
                break;
            case "*" :
                result =  operand1 * operand2;
                break;
            case "/" :
                if (operand2 == 0) {
                    return 0;
                }
                result =  operand1 / operand2;
                break;
            default:
        }
        return result;
    }

    private static String[] transformExpression(String newInfixExpression) {
        // 运算符栈
        Stack<String> operatorStack = new Stack<>();
        // 操作数缓冲区
        StringBuffer tempOperandBuffer = new StringBuffer();
        // 后缀表达式
        String postfixExpression = null;
        // 后缀表达式数组
        String[] postExpressionArray = new String[newInfixExpression.length()];
        // 数组下标
        int index = 0;
        // 存储数组的标识
        boolean flag = false;

        // 遍历中缀表达式
        for (int i = 0; i < newInfixExpression.length(); i++) {
            // 当前字符转换为字符串, 存储栈
            String currentStr = String.valueOf(newInfixExpression.charAt(i));
//            System.out.println("当前字符为: " + currentStr);
            switch (currentStr) {
                // 如果是加号运算符或者减号运算符
                // 根据转换规则, 需判断当前运算符与栈顶元素运算符的优先级, 并将当前运算符入栈
                case "+":
                case "-":
                    // 栈顶元素如果不是左括号 "(", 则依次出栈并输出
                    while (!operatorStack.empty()) {
                        if (!"(".equals(operatorStack.peek())) {
                            postExpressionArray[index++] = operatorStack.peek();
                            operatorStack.pop();
                        } else {
                            break;
                        }
                    }
                    // 处理完出战的逻辑或者栈为空, 则将当前运算符入栈
                    operatorStack.push(currentStr);
                    flag = true;
                    break;

                // 如果是乘号运算符或者除号运算符
                // 根据转换规则, 需判断当前运算符与栈顶元素运算符的优先级, 并将当前运算符入栈
                case "*":
                case "/":
                    while (!operatorStack.empty()) {
                        // 如果栈顶元素的优先级与当前运算符的优先级相同, 即栈顶元素为 "*" 或 "/", 则栈顶元素出栈并输出
                        if ("*".equals(operatorStack.peek()) || "/".equals(operatorStack.peek())) {
                            postExpressionArray[index++] = operatorStack.peek();
                            operatorStack.pop();
                        } else {
                            break;
                        }
                    }
                    operatorStack.push(currentStr);
                    flag = true;
                    break;

                // 如果是左括号, 直接入栈
                case "(":
                    operatorStack.push(currentStr);
                    flag = true;
                    break;

                // 如果是右括号, 则匹配左括号
                case ")":
                    while (!operatorStack.empty()) {
                        if (!tempOperandBuffer.toString().isEmpty()) {
                            postExpressionArray[index++] = tempOperandBuffer.toString();
                            tempOperandBuffer = new StringBuffer();
                            flag = false;
                        }
                        // 将距离栈顶元素最近的左括号之前的运算符全部出栈并输出, 并将左括号也输出
                        if (!"(".equals(operatorStack.peek())) {
                            postExpressionArray[index++] = operatorStack.peek();
                            operatorStack.pop();
                        } else {
                            operatorStack.pop();
                            break;
                        }
                    }
                    break;

                // 如果是数字, 则直接记录进后缀表达式缓冲区中
                default:
                    if (flag) {
                        if (!tempOperandBuffer.toString().isEmpty()) {
                            postExpressionArray[index++] = tempOperandBuffer.toString();
                        }
                        tempOperandBuffer = new StringBuffer(currentStr);
                        flag = false;
                    } else {
                        tempOperandBuffer.append(currentStr);
                    }
            }
        }
        // 处理操作数缓冲区的内容
        if (!tempOperandBuffer.toString().isEmpty()) {
            postExpressionArray[index++] = tempOperandBuffer.toString();
        }
        // 遍历完中缀表达式之后, 将栈中元素依次输出
        while (!operatorStack.empty()) {
            postExpressionArray[index++] = operatorStack.peek();
            operatorStack.pop();
        }
        return postExpressionArray;
    }

    private static String handlerParentheses(String infixExpression) {
        return infixExpression.replace("[", "(")
                .replace("]", ")").replace("{", "(")
                .replace("}", ")");
    }

    public static void main(String[] args) {
//        String infixExpression = "6*8";
        String infixExpression = "800/{5*[(34+46)/8]}";
        mixingOperation(infixExpression);
    }

}