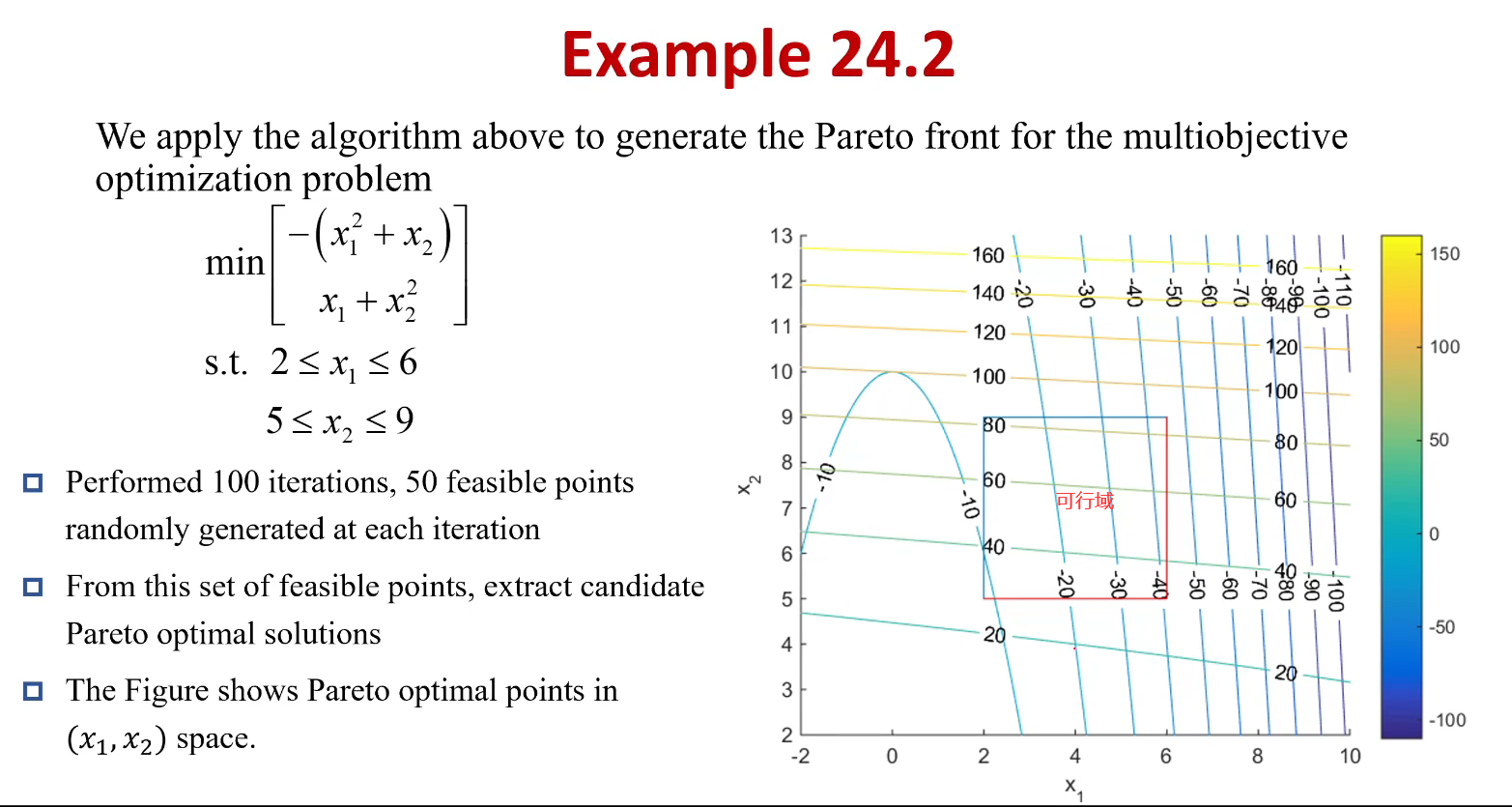
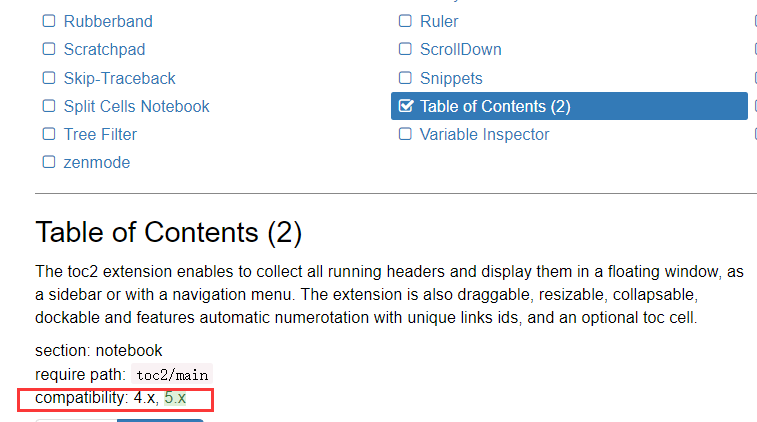
0 前言
-
多目标优化在推荐系统、物流配送、路径规划等中有广泛的应用
-
一些多目标优化算法主要就是求解问题的 Pareto 前沿或者近似前沿。从目标空间来看,就是他的边界了。
1. 优化问题
1.1 无约束的单目标优化问题
m
i
n
x
f
(
x
)
,
x
∈
R
N
(1)
min_x \quad f(x), x \in R^N \tag{1}
minxf(x),x∈RN(1)
其中,x 的取值为 n 维实数空间 RN, f(x) 为连续一阶可导函数
1.2 无约束的多目标优化问题
m
i
n
x
F
(
x
)
=
[
f
1
(
x
)
,
f
2
(
x
)
,
.
.
.
,
f
K
(
x
)
]
,
x
∈
R
N
(2)
min_x \quad F(x) = [f_1(x), f_2(x), ... , f_K(x)], x \in R^N \tag{2}
minxF(x)=[f1(x),f2(x),...,fK(x)],x∈RN(2)
其中,K 为子目标的个数,
x
x
x 的取值为 N 维实数空间,
f
k
(
x
)
f_k(x)
fk(x) 为连续一阶可导函的子目标函数。
1.3 带约束的单目标优化问题
m
i
n
x
f
(
x
)
min_x \quad f(x)
minxf(x)
s
.
t
.
g
i
(
x
)
≥
0
,
i
∈
[
1
,
M
]
(3)
s.t. g_i(x) \geq 0, i \in [1, M] \tag{3}
s.t.gi(x)≥0,i∈[1,M](3)
h
j
(
x
)
=
0
,
j
∈
[
1
,
L
]
h_j(x) = 0, j \in [1, L]
hj(x)=0,j∈[1,L]
其中
s
.
t
.
s.t.
s.t. 为 subject to 的缩写,表示受限于的意思
令
D
D
D 为上述多目标优化问题的可行域,即:
D
=
{
x
∣
g
i
(
x
)
≥
0
,
i
∈
[
1
,
M
]
,
h
j
(
x
)
=
0
,
j
∈
[
1
,
L
]
}
D = \{ x | g_i(x) \geq 0, i \in [1, M], h_j(x) = 0, j \in [1, L]\}
D={x∣gi(x)≥0,i∈[1,M],hj(x)=0,j∈[1,L]}
1.4 带约束的多目标优化问题
带约束的多目标问题 MOP (multi-objective optimization problem)
m
i
n
x
F
(
x
)
=
[
f
1
(
x
)
,
f
2
(
x
)
,
.
.
.
,
f
K
(
x
)
]
min_x \quad F(x) = [f_1(x), f_2(x), ... , f_K(x)]
minxF(x)=[f1(x),f2(x),...,fK(x)]
s
.
t
.
g
i
(
x
)
≥
0
,
i
∈
[
1
,
M
]
(4)
s.t. g_i(x) \geq 0, i \in [1, M] \tag{4}
s.t.gi(x)≥0,i∈[1,M](4)
h
j
(
x
)
=
0
,
j
∈
[
1
,
L
]
h_j(x) = 0, j \in [1, L]
hj(x)=0,j∈[1,L]
令
D
D
D 为上述多目标优化问题的可行域,即
D
=
{
x
∣
g
i
(
x
)
≥
0
,
i
∈
[
1
,
M
]
,
h
j
(
x
)
=
0
,
j
∈
[
1
,
L
]
}
D = \{ x | g_i(x) \geq 0, i \in [1, M], h_j(x) = 0, j \in [1, L]\}
D={x∣gi(x)≥0,i∈[1,M],hj(x)=0,j∈[1,L]}
2. 多目标优化的解集:解集定义
-
对于多目标优化问题 MOP,通常不存在解 x ∗ ∈ D x^* \in D x∗∈D,使得目标 f i ( x ) , ∀ i ∈ [ 1 , K ] f_i(x), \forall i \in [1, K] fi(x),∀i∈[1,K], 同时达到最小值
-
在描述 MOP 的解集之前,我们先来定义多目标里面的相等、严格小于、小于、小于且不相等的含义:
-
设 R N R^N RN 为 N N N 维实向量空间, y = ( y 1 , y 2 , . . . , y N ) T , z = ( z 1 , z 2 , . . . , z N ) T y = (y_1, y_2, ..., y_N)^T, z = (z_1, z_2, ..., z_N)^T y=(y1,y2,...,yN)T,z=(z1,z2,...,zN)T
f ( n ) = { 相 等 y = z ⇔ y i = z i , i = 1 , 2 , . . . , N 严 格 小 于 y < z ⇔ y i = z i , i = 1 , 2 , . . . , N 小 于 y < z ⇔ y i = z i , i = 1 , 2 , . . . , N 小 于 且 不 相 等 y ≤ z ⇔ y i = z i , i = 1 , 2 , . . . , N , 且 y ≠ z (5) f(n) = \begin{cases} 相等 & \text{$y = z \Leftrightarrow y_i = z_i, i = 1, 2, ..., N$ } \\ 严格小于& \text{$y < z \Leftrightarrow y_i = z_i, i = 1, 2, ..., N \tag{5} $ } \\ 小于 & \text{$y < z \Leftrightarrow y_i = z_i, i = 1, 2, ..., N$ } \\ 小于且不相等 & \text{$y \leq z \Leftrightarrow y_i = z_i, i = 1, 2, ..., N, 且\quad y \neq z$ } \\ \end{cases} f(n)=⎩⎪⎪⎪⎨⎪⎪⎪⎧相等严格小于小于小于且不相等y=z⇔yi=zi,i=1,2,...,N y<z⇔yi=zi,i=1,2,...,N y<z⇔yi=zi,i=1,2,...,N y≤z⇔yi=zi,i=1,2,...,N,且y=z (5)
2.1 可行解
对于某个 x ∈ X x \in X x∈X,如果 x 满足(4)中的约束条件 g i ( x ) ≥ 0 , i ∈ [ 1 , M ] 和 h j ( x ) = 0 , j ∈ [ 1 , L ] g_i(x) \geq 0, i \in [1, M] 和 h_j(x) = 0, j \in [1, L] gi(x)≥0,i∈[1,M]和hj(x)=0,j∈[1,L] 则称 x x x 为可行解
两个目标函数
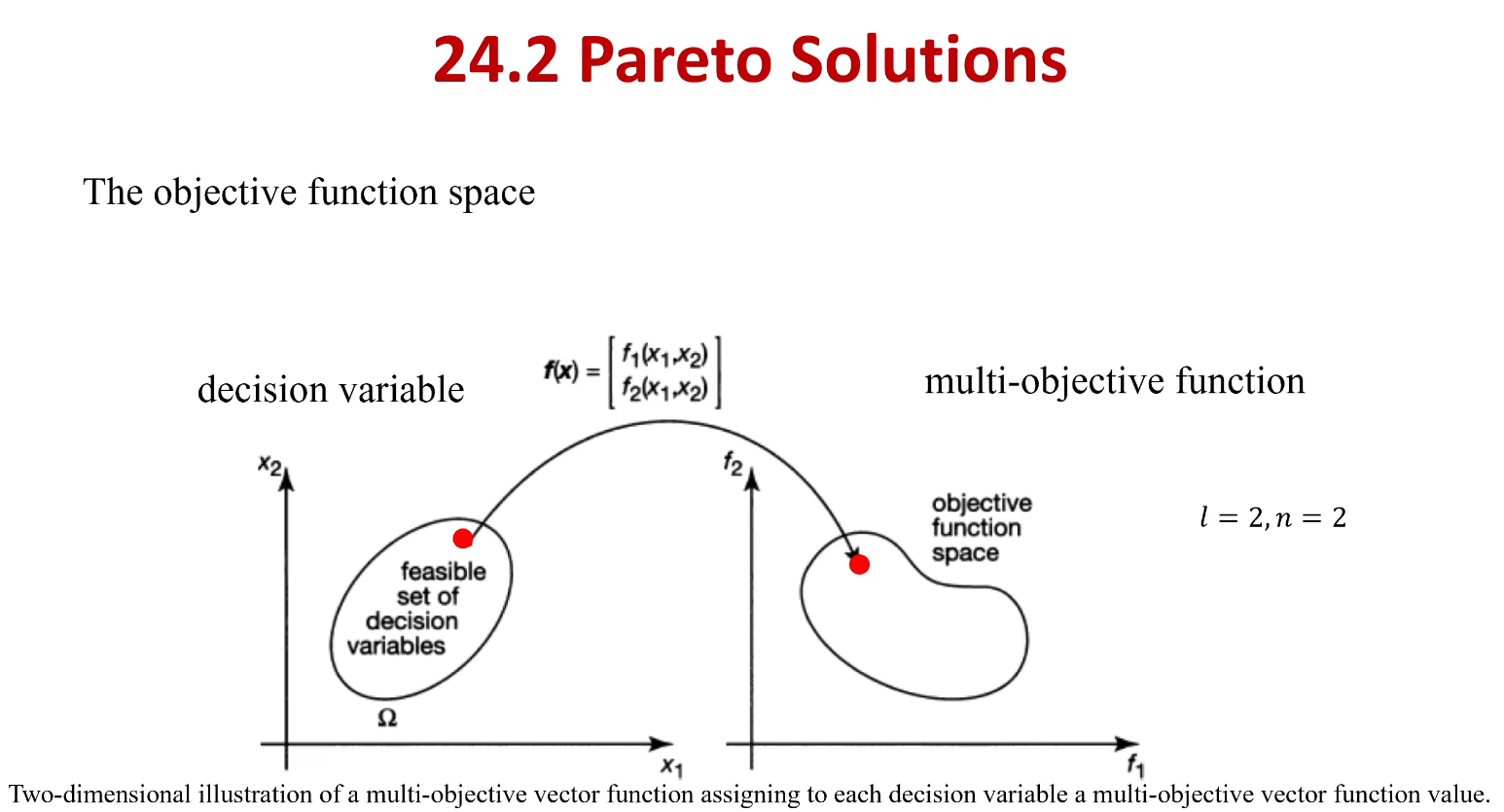
三个目标函数
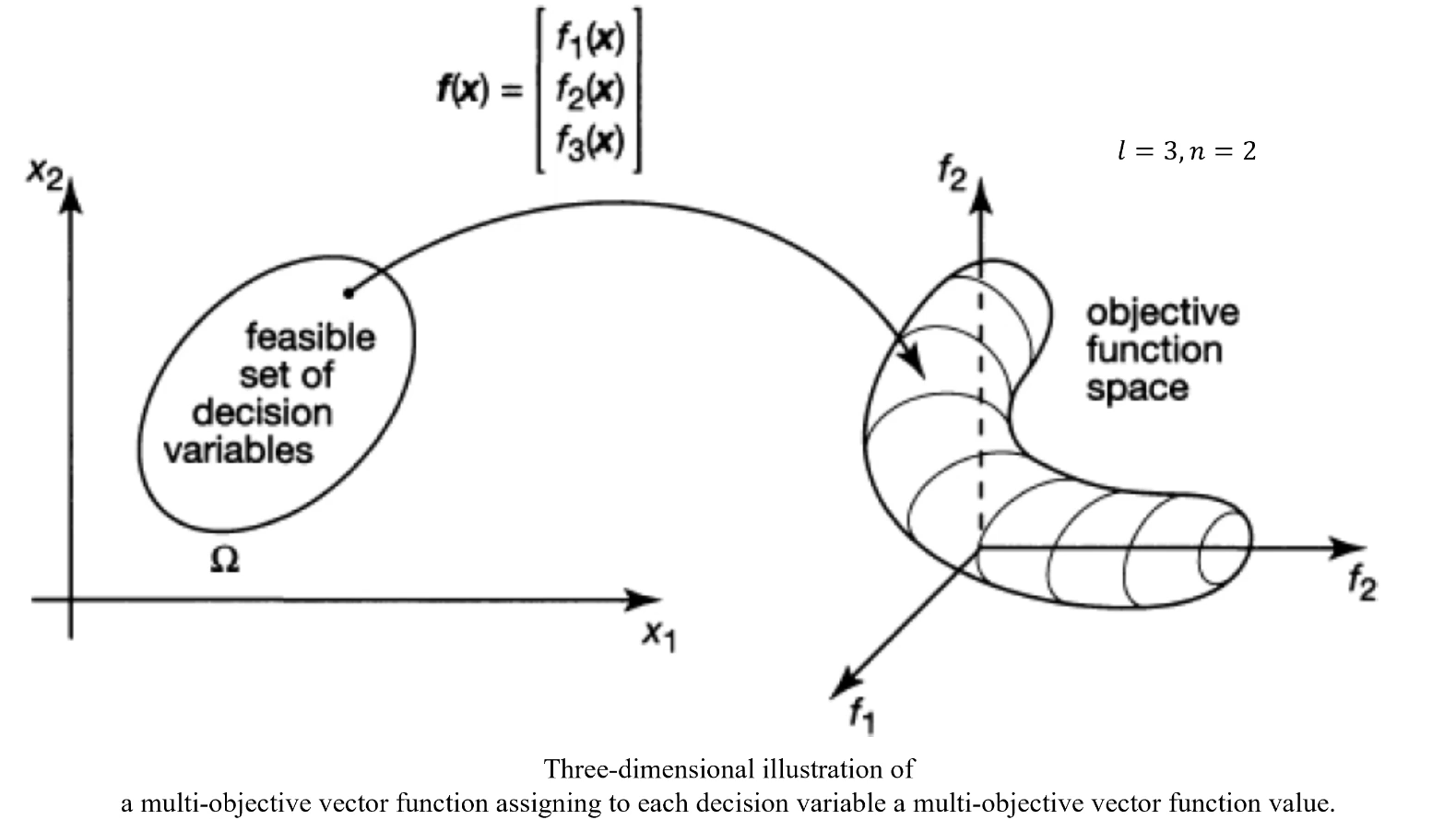
2.2 可行解集合
由 X X X 中的所有的可行解组成的集合称为可行解集合,记为 X f X_f Xf,且 X f ⊆ X X_f \subseteq X Xf⊆X
2.3 Pareto 支配 (Pareto Dominance)
定义: ∀ x 1 , x 2 ∈ X f \forall x_1, x_2 \in X_f ∀x1,x2∈Xf,如果对于 ∀ i ∈ [ 1 , M ] \forall i \in [1, M] ∀i∈[1,M],都有 f i ( x 1 ) ≤ f i ( x 2 ) f_i(x_1) \leq f_i(x_2) fi(x1)≤fi(x2) 并且, ∃ j ∈ [ 1 , L ] \exists j \in [1, L] ∃j∈[1,L],使得 f j ( x 1 ) < f j ( x 2 ) f_j(x_1) < f_j(x_2) fj(x1)<fj(x2) 则称 x 1 x_1 x1 支配 x 2 x_2 x2,也称 x 1 x_1 x1 是 Pareto 占优的


2.4 Pareto 最优解
一个解 x ∗ ∈ X f x^* \in X_f x∗∈Xf,若 ¬ ∃ x ∈ X f : x 支 配 x ∗ \neg\exists x \in X_f:x 支配 x^* ¬∃x∈Xf:x支配x∗,则 x ∗ x^* x∗ 被称为 Pareto 最优解(或非支配解)
2.5 Pareto 最优解集
Pareto 最优解集是所有 Pareto 最优解的集合,定义如下:
P
∗
=
{
x
∗
∣
¬
∃
x
∈
X
f
:
x
支
配
x
∗
}
P^* = \{x^*|\neg\exists x \in X_f:x 支配 x^*\}
P∗={x∗∣¬∃x∈Xf:x支配x∗}
2.6 Pareto 前沿面
Pareto 最优解集
P
∗
P^*
P∗ 中的所有 Pareto 最优解对应的目标矢量组成的曲面称为 Pareto 前沿面
P
F
∗
PF^*
PF∗:
P
F
∗
=
{
F
(
x
∗
)
=
(
f
1
(
x
∗
)
,
f
1
(
x
∗
)
,
.
.
.
,
f
m
(
x
∗
)
)
T
∣
x
∗
∈
P
∗
}
PF^* = \{F(x^*) = (f_1(x^*), f_1(x^*), ..., f_m(x^*))^T|x^* \in P^*\}
PF∗={F(x∗)=(f1(x∗),f1(x∗),...,fm(x∗))T∣x∗∈P∗}
3. 实例阐述 Pareto
3.1 第一个实例
1:解 A 优于解 B(解 A 强帕累托支配解 B)
假设现在有两个目标函数,解 A 对应的目标函数值都比解 B 对应的目标函数值好,则称解A比解 B 优越,也可以叫做解 A 强帕累托支配解 B,举个例子
下图中代表的是两个目标的的解的情况,横纵坐标表示两个目标函数值,E 点表示的解所对应的两个目标函数值都小于 C,D 两个点表示的解所对应的两个目标函数值,所以解 E 优于解 C,D
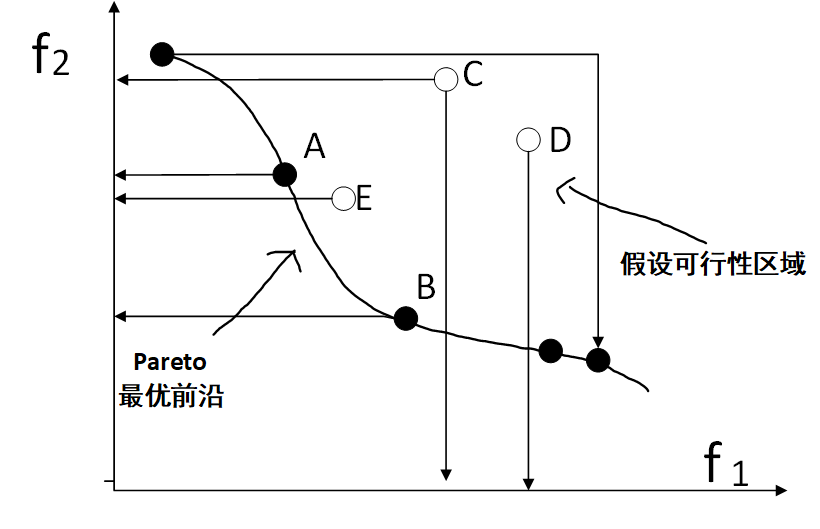
2:解 A 无差别于解 B(解 A 能帕累托支配解 B)A,B两点严格意义上是非支配关系
同样假设两个目标函数,解 A 对应的一个目标函数值优于解 B 对应的一个目标函数值,但是解 A 对应的另一个目标函数值要差于解 B 对应的一个目标函数值,则称解 A 无差别于解B,也叫作解 A 能帕累托支配解 B,举个例子,还是上面的图,点 C 和点 D 就是这种情况,C 点在第一个目标函数的值比 D 小,在第二个函数的值比 D 大。
3:最优解
假设在设计空间中,解 A 对应的目标函数值优越其他任何解,则称解 A 为最优解,举个例子,下图的 x 1 x_1 x1 就是两个目标函数的最优解,使两个目标函数同时达到最小,但实际生活中这种解是不可能存在的,由此提出了帕累托最优解
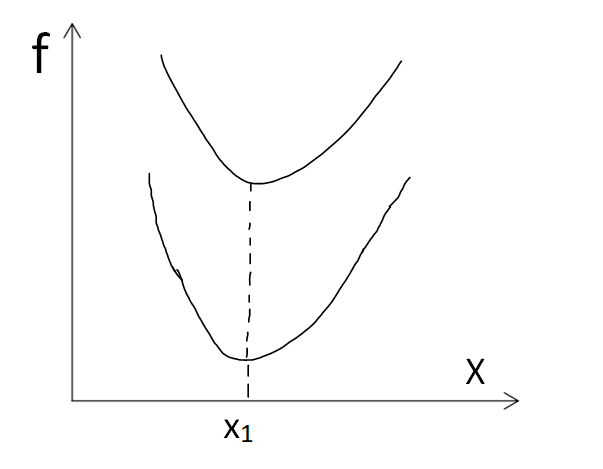
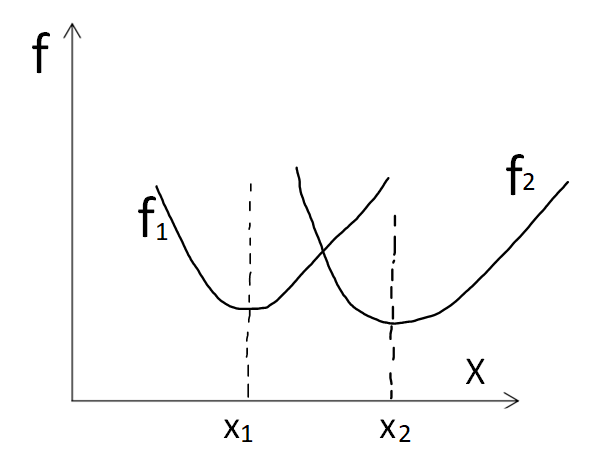
4:帕累托最优解
同样假设两个目标函数,对于解 A 而言,在变量空间中找不到其他的解能够优于解A(这里的优于一定要两个目标函数值都优于 A 对应的函数值),那么解 A 就是帕累托最优解,举个例子,下图中应该找不到比 对应的目标函数都小的解了吧,即找不到一个解优于 x 1 x_1 x1 了,同理也找不到比 x 2 x_2 x2 更优的解了,所以这两个解都是帕累托最优解,实际上, 这个范围的解都是帕累托最优解。因此对于多目标优化问题而言,帕累托最优解只是问题的一个可接受解,一般都存在多个帕累托最优解,这个时候就需要自己决策了。
5:帕累托最优前沿
还是那张图 ,如下图所示,更好的理解一下帕累托最优解,实心点表示的解都是帕累托最优解,所有的帕累托最优解构成帕累托最优解集,这些解经目标函数映射构成了该问题的 Pareto 最优前沿或 Pareto 前沿面,即帕累托最优解对应的目标函数值就是帕累托最优前沿。

对于两个目标的问题,其 Pareto 最优前沿通常是条线。而对于多个目标,其 Pareto 最优前沿通常是一个超曲面。
3.2 第二个实例
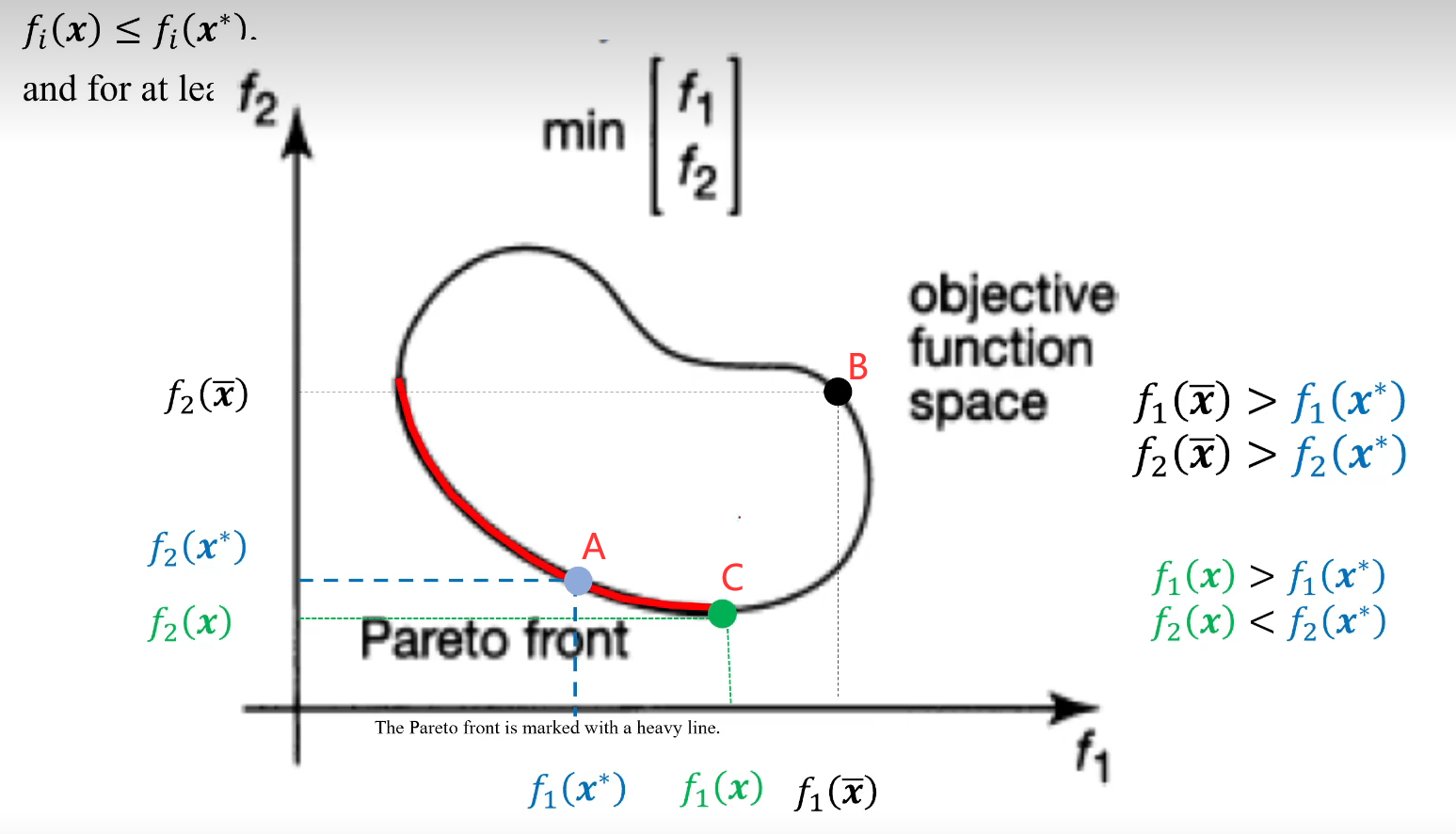
在求目标函数 f 1 , f 2 f_1, f_2 f1,f2,的最小值的时候,当 A 与 B 相比 f 1 ( x ∗ ) < f 1 ( x ‾ ) f_1(x^*) < f_1(\overline{x}) f1(x∗)<f1(x),且 f 2 ( x ∗ ) < f 2 ( x ‾ ) f_2(x^*) < f_2(\overline{x}) f2(x∗)<f2(x) ,所以 B 不支配 A,而 A 支配 B, A 与 C 相比, f 2 ( x ) < f 2 ( x ∗ ) f_2(x) < f_2(x^*) f2(x)<f2(x∗),若 f 1 ( x ) < f 1 ( x ∗ ) f_1(x) < f_1(x^*) f1(x)<f1(x∗),则 C 支配 A,但是 f 1 ( x ) > f 1 ( x ∗ ) f_1(x) > f_1(x^*) f1(x)>f1(x∗),所以没有支配关系,属于非支配关系
分析可以知道,红色曲线上的点,在进行内部点之间比较的时候,如果一个点其中一个函数值小于另一个点对应的函数值时,那么此点的另一个函数值一定大于另一个对应的函数值
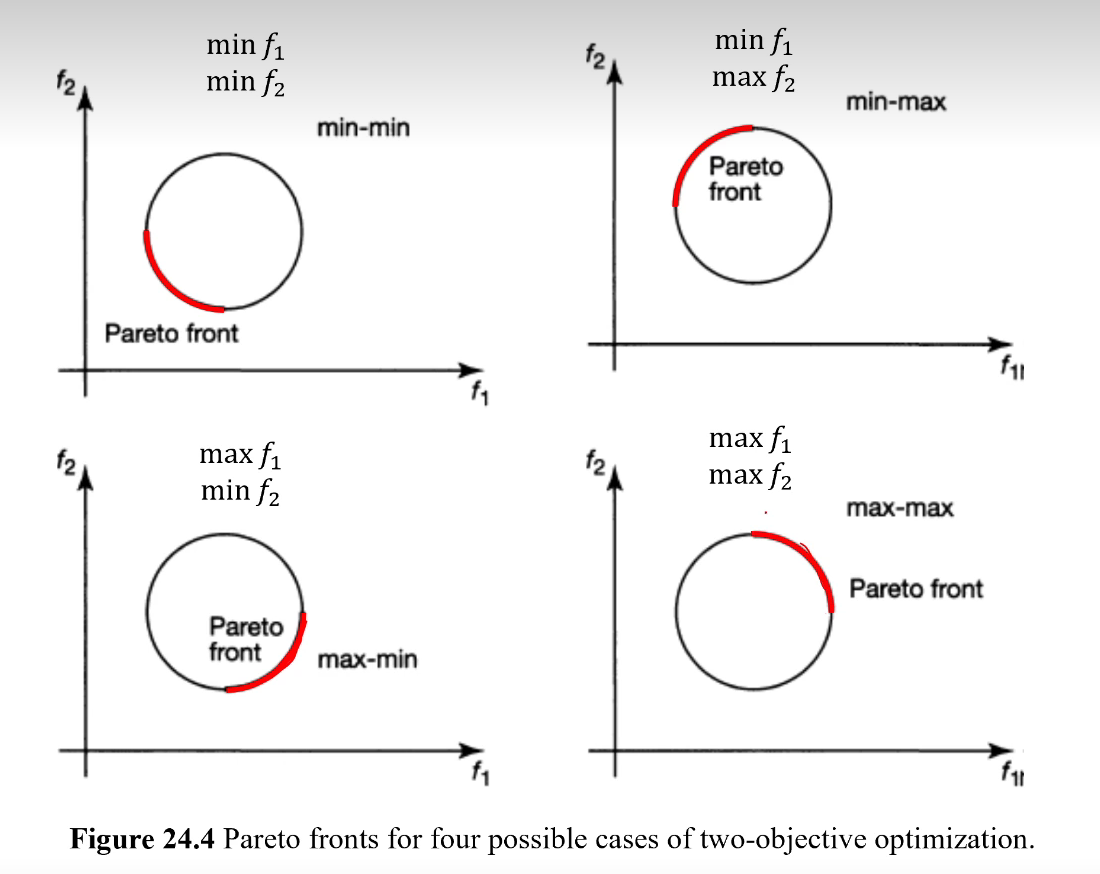
不同情况下的 Pareto 最优前沿
4. Pareto 算法


转化为单目标函数


将其中一个函数作为目标函数,其他函数作为约数条件

5. Pareto 的计算
5.1 第一个实例
假设有两个目标目标函数,两个变量
x
1
,
x
2
x_1, x_2
x1,x2,对应的解集为
f
(
x
1
)
,
f
(
x
2
)
f(x_1), f(x_2)
f(x1),f(x2)

1 号 与 2 号比,目标函数,2 号均比 1 号小,加入 pareto 点集, 3 号 和 2 号比,第一个目标函数小于 2 号,第二个目标函数大于 2 号,加入 pareto 点集

第 5 行数据再与 Pareto 候选集进行比较时,即 5 与 3 比较,发现 13 < 19 并且 45 < 53, 所以 3 被 5 支配,把 3 号点去掉,留下 5 号选入 Pareto 点集
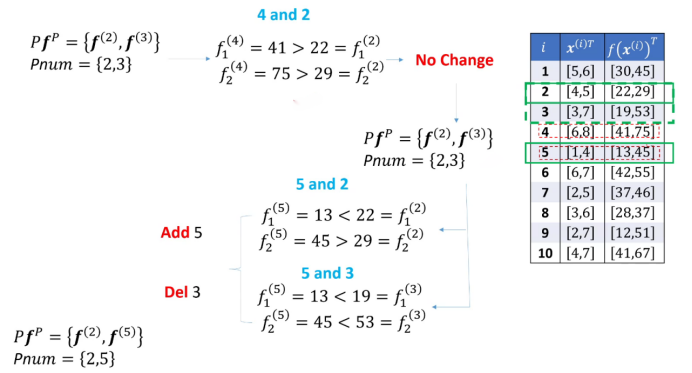

最终的 pareto 前沿计算结果为:2, 9, 5
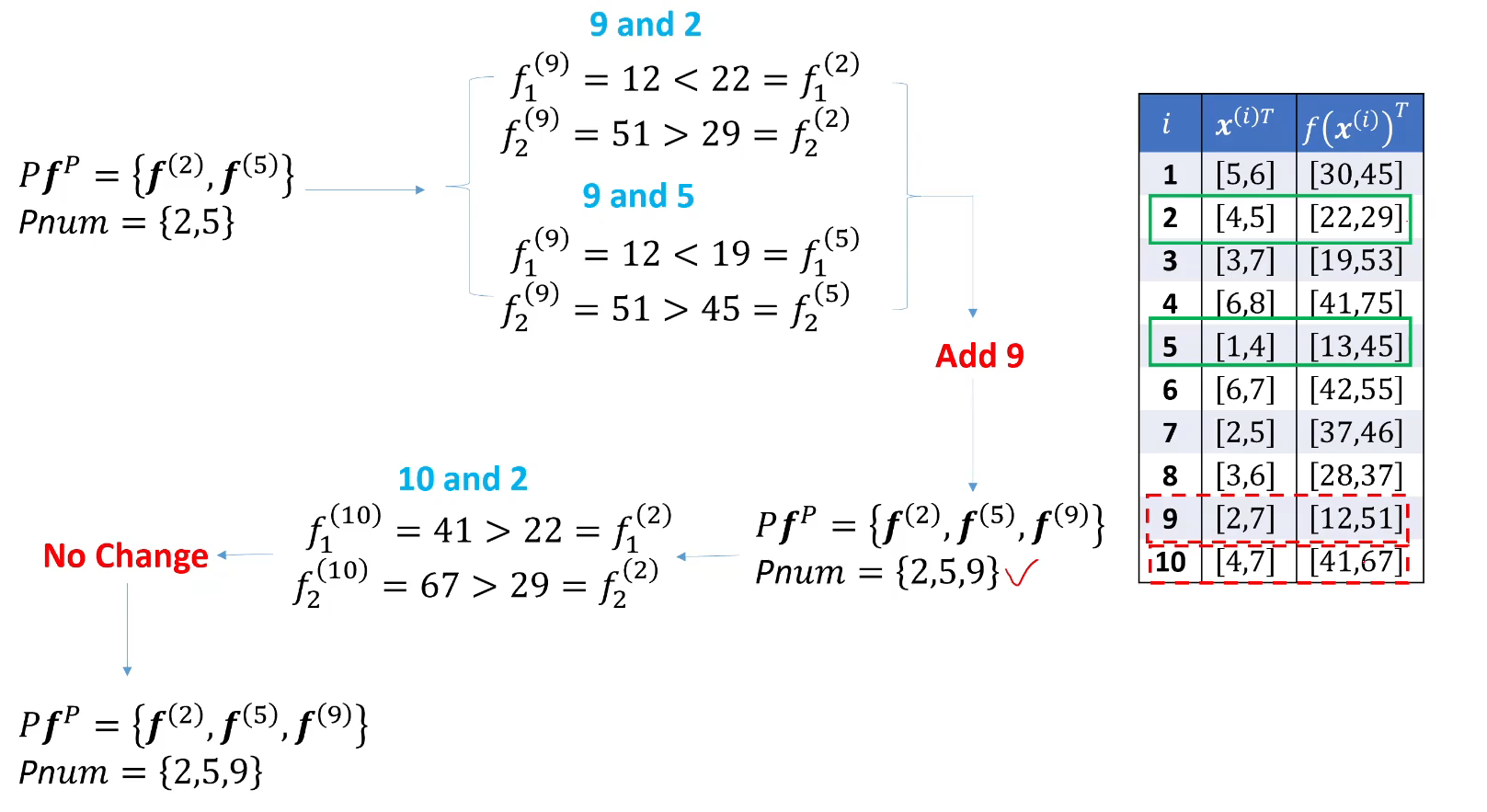
5.2 第二个实例
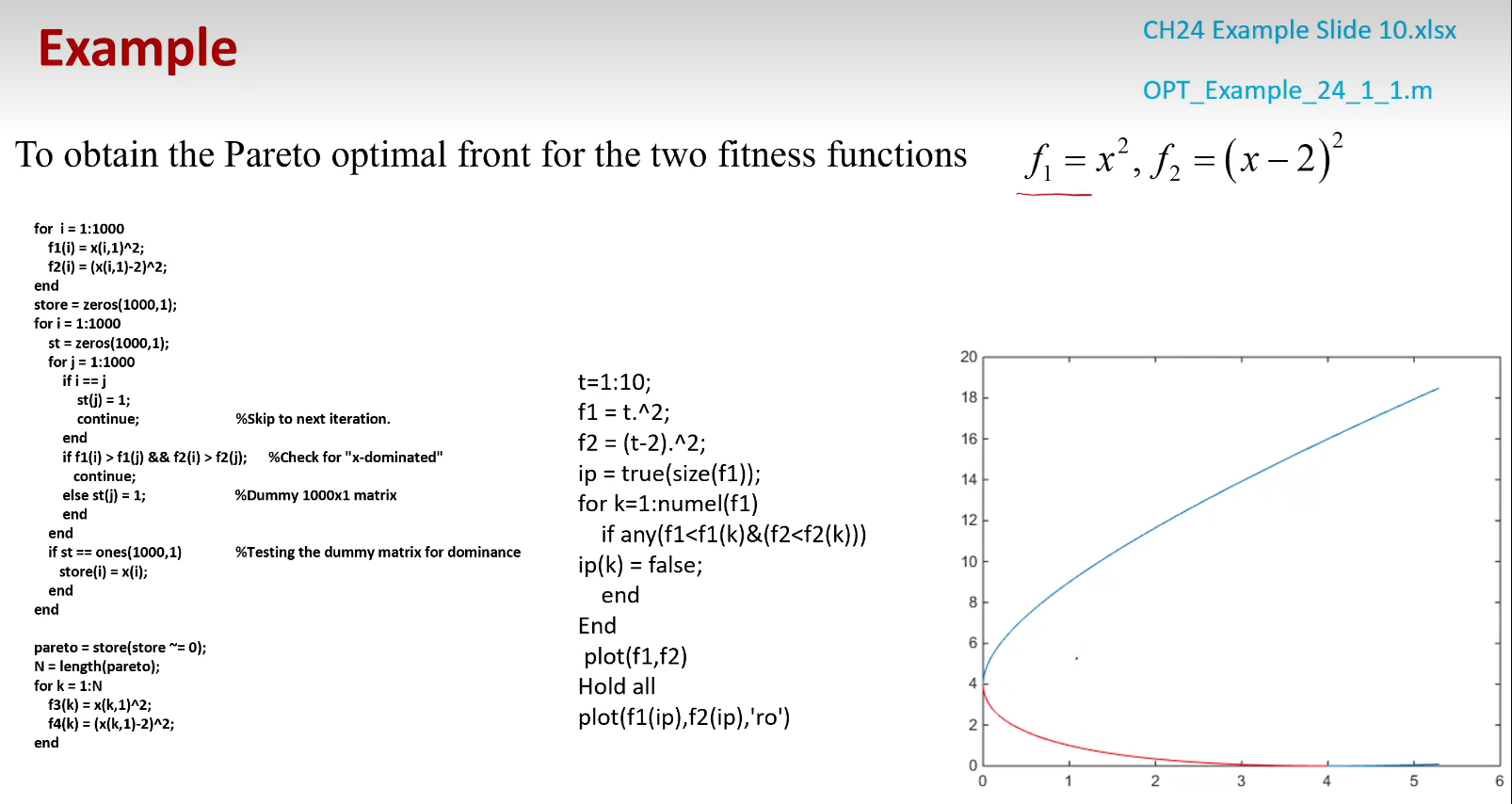
5.3 第三个实例