目录
介绍
节点的定义
AVLTree结构
Insert
插入节点
调节平衡因子
void rotateR(node* parent)
void rotateL(node* parent)
void rotateRL(node* parent)
void rotateLR(node* parent)
void InOrder()
int height()
int size()
bool isBalance()
介绍
- 如果是有序插入BSTree,高度就是n,那么查找的时间复杂度就是n;通过旋转,来调整高度就是AVLTree
节点的定义
template<class K, class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left; // <K, V> 要不要写
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V> _kv;
int _bf;
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};- 类+模板才是类型
AVLTree结构
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> node;
public:
private:
node* _root = nullptr;
};- 必须初始化_root;不然会影响Insert第一个节点的插入
Insert
插入节点
- 要给 _root 赋值上第一个节点的地址
- 通过parent节点来链接新的节点,parent节点初始化为cur就行,可以不初始化为nullptr,因为cur一定不是nullptr;所以不用担心后面parent会解引用空指针
bool Insert(pair<K, V> kv) // return
{
if (_root == nullptr)
{
_root = new node(kv);
return true;
}
node* cur = _root;
node* parent = cur;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false; //
}
}
cur = new node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//调节平衡因子
}调节平衡因子
- 新增在右树,parent 的 bf++
- 改变完parent,判断bf
- bf == 0就直接跳出,调整完毕;因为0是由1或者-1变来的,变为0就是parent的左右树高度由一边高1变为相等(也就是矮的那边多了一个节点),自然不会影响pparent的高度
- bf == 1 || bf == -1 说明parent的高度变了,那么pparent的高度也变了,所以需要往上更新pparent的bf
- while的跳出的条件;cur->_parent:我的调整bf原因是子影响父,所以父不为空就调整;当然,条件也可以为parent
bool Insert(pair<K, V> kv) // return
{
//插入...
//调节bf
while (cur->_parent)
{
if (parent->_right == cur)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
if (parent->_bf == -2 && cur->_bf == -1)
{
rotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1)
{
rotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
rotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
rotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
assert(false);
}
}
}void rotateR(node* parent)
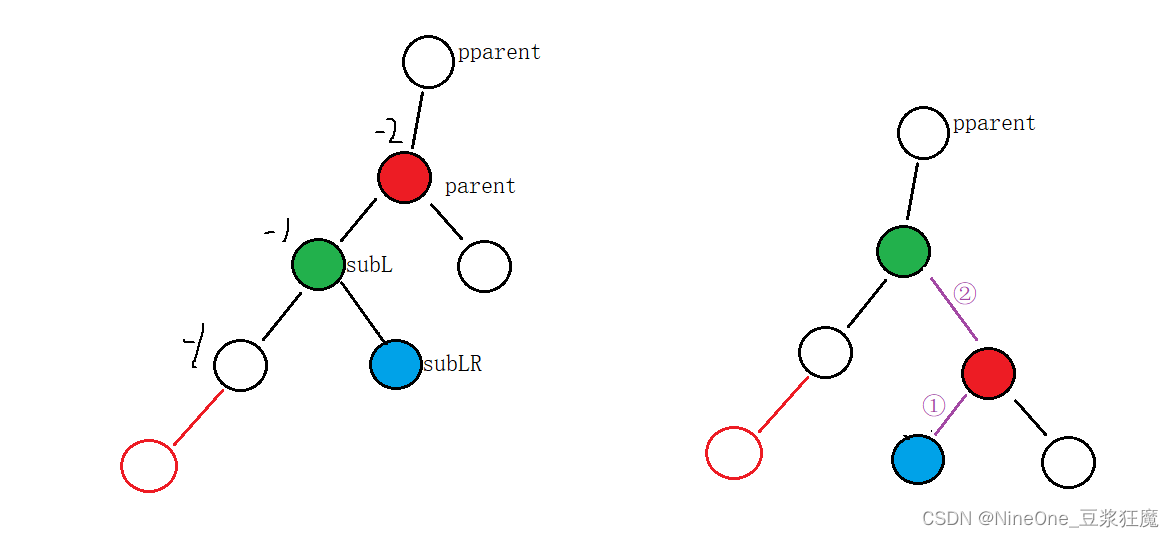
操作
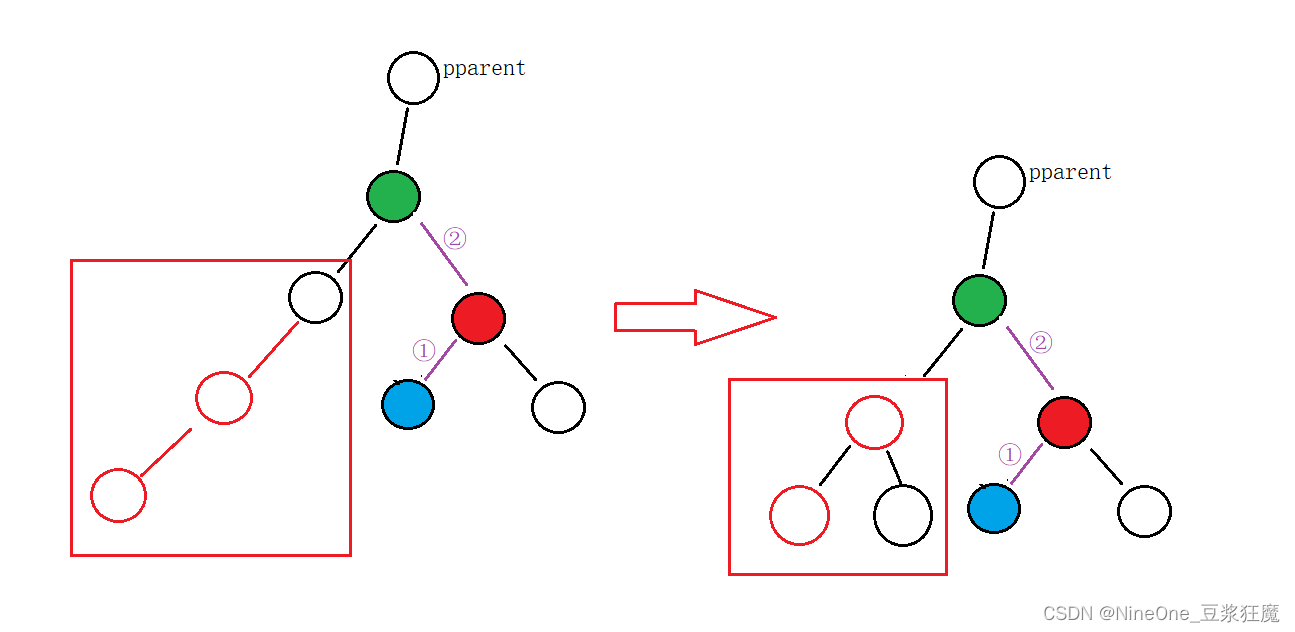
- 红圈是新增节点
- 插入到左边,左边高了,为了降低parent这个子树,可以将parent变成subL的右子树,达到将高度的目的
- 调整指向的顺序是先①在②,这样更有旋转的感觉;先②再①当然也可以,毕竟这4个节点都被定义了,都可以直接拿到
- 对parent的讨论:是否为 _root
- 一共调整4个节点,那么两两之间的父子链接操作就有3次
解释
- 插在最左边这个树的左右都不影响,因为parent不连接这边
- 最后就是改bf,parent和subL一定是0吗?parent的左右子树要么都为空,要么都只有一个节点;
- 这个右旋的情况实际上只有两种;因为节点是一个个插入的,所以每一次插入都会判断是否旋转;你所看到的十几种情况的,我觉得都不准确,因为早就发生了旋转,他们所对应的那种树型根本就不会存在
void rotateR(node* parent)
{
node* subL = parent->_left;
node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
node* pparent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root == subL;
}
else
{
if (pparent->_kv.first < subL->_kv.first)
{
pparent->_right = subL;
}
else
{
pparent->_left = subL;
}
}
subL->_parent = pparent;
parent->_bf = subL->_bf = 0;
}void rotateL(node* parent)
操作
- 和左旋一模一样,可以理解为镜像反转一下
void rotateL(node* parent)
{
node* subR = parent->_right;
node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
node* pparent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
}
else
{
if (pparent->_kv.first < subR->_kv.first)
{
pparent->_right = subR;
}
else
{
pparent->_left = subR;
}
}
subR->_parent = pparent;
parent->_bf = subR->_bf = 0;
}void rotateRL(node* parent)
操作
- 对平衡因子的调控,先右左旋,旋完之后bf都为0
- 然后分情况调控bf
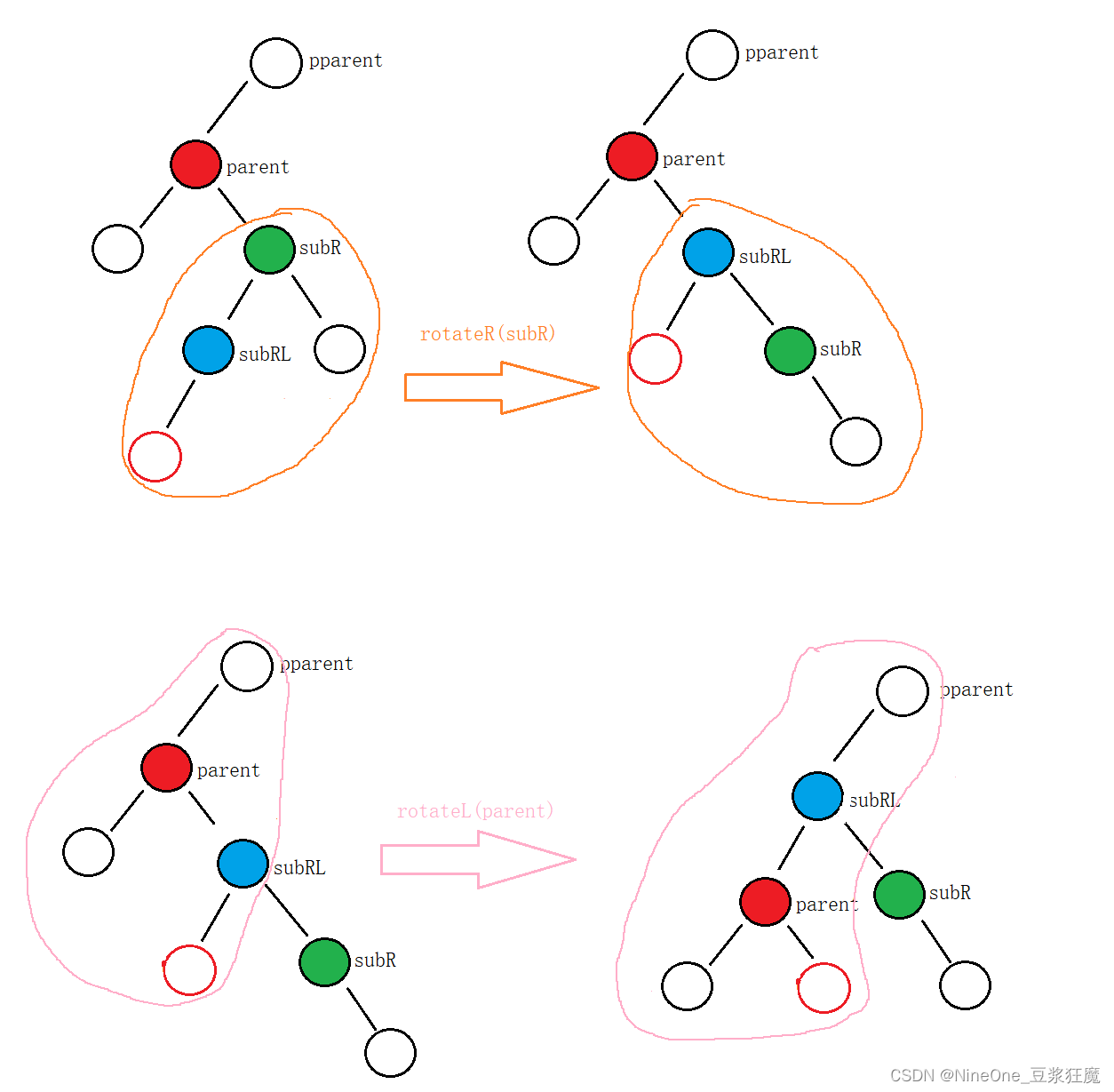
解释
- 对新插入的节点在subRL的左边和右边是不一样的
- 插到左边 (即bf == -1),最后会给到parent,那么sub左边就会空缺,subR->_bf就要改成1
- 插到右边 (即bf == 1) ,最后会给到subR,那么parent右边就会空缺,parent->_bf就要改成-1
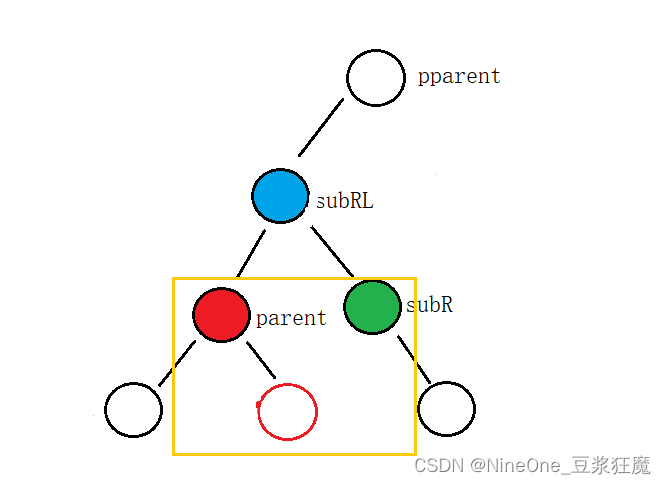
- 还有一种就是bf == 0(即subRL是新插入的节点)这时候parent和subR对应的左右子树都为空,一定为空,不然不会发生右左旋
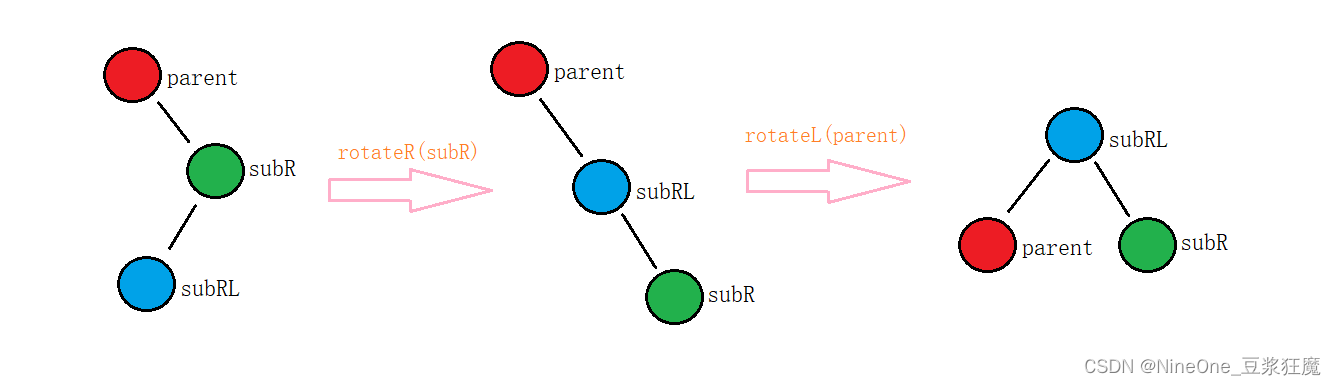
void rotateRL(node* parent)
{
node* subR = parent->_right;
node* subRL = subR->_left;
int bf = subRL->_bf;
rotateR(subR);
rotateL(parent);
if (bf == 0)
{
//parent->_bf = 0;
//subR->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = -1;
//subR->_bf = 0;
}
else if (bf == -1)
{
//parent->_bf = 0;
subR->_bf = 1;
}
else
{
assert(false);
}
}void rotateLR(node* parent)
解释
- 镜像对称,平衡因子反一下就行
void rotateLR(node* parent)
{
node* subL = parent->_left;
node* subLR = subL->_right;
int bf = subLR->_bf;
rotateL(subL);
rotateR(parent);
if (bf == 0)
{
//parent->_bf = 0;
//subL->_bf = 0;
}
else if (bf == 1)
{
//parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
//subL->_bf = 0;
}
else
{
assert(false);
}
}void InOrder()
public:
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}int height()
public:
int height()
{
return _height(_root);
}
private:
int _height(node* root)
{
if (root == nullptr)
return 0;
return max(_height(root->_left), _height(root->_right)) + 1;
}int size()
public:
int size()
{
return _size(_root);
}
private:
int _size(node* root)
{
if (root == nullptr)
return 0;
return _size(root->_left) + _size(root->_right) + 1;
}bool isBalance()
先序
public:
bool isBalance()
{
return _isBalance(_root);
}
private:
bool _isBalance(node* root)
{
if (root == nullptr)
return true;
int leftHeight = _height(root->_left);
int rightHeight = _height(root->_right);
if (abs(leftHeight - rightHeight) >= 2)
return false;
return _isBalance(root->_left) && _isBalance(root->_right);
}后序
public:
bool isBalanced()
{
int height = 0;
return _isBalance(_root, height);
}
private:
bool _isBalance(node* root, int& height)
{
if (root == nullptr)
{
height = 0;
return true;
}
int leftHeight = 0;
int rightHeight = 0;
bool isLeftBalanced = _isBalance(root->_left, leftHeight);
bool isRightBalanced = _isBalance(root->_right, rightHeight);
height = max(leftHeight, rightHeight) + 1;
if (!isLeftBalanced || !isRightBalanced || abs(leftHeight - rightHeight) >= 2)
{
return false;
}
return true;
}- 后序遍历的顺序是先处理左子树,再处理右子树,最后处理当前节点。不会重复计算子树的高度。