导语:相比矩阵,用四元数处理3D旋转的优势是毋庸置疑的,但由于概念复杂,难于理解,一直令我摸不着头脑。最近学习更是发现在机器人、无人机、SLAM等先进领域,四元数被当成实数、整数这样的基础,所以决定努力补一补这块的知识点。全部内容都来自B站/知乎上的大佬们,这只是本人学习有所感悟后,梳理出来的总结。
一、四元数是如何诞生的?
可能四元数的由来大家都看过很多遍。四元数(Quaternions),是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865)提出的,他最初的想法是:即然在实数上再扩展一个虚数,就能表示二维平面上所有的点,那么再扩展一个虚数是不是就可以表示三维空间上所有的点?这个想法简单写下来就是这样:z = a + b·i + c·j
但是用这个(三元数)方式去表示三维坐标,那么相乘的结果会得出一项 i · j ,两个不同维度的相乘是多少?如果 i · j 直接等于 -1,那么 i · i = -1, j · j = -1,那岂不是 i = j?
就上面这个问题,哈密顿思考了很久。有一天这位学者行走在大桥上,看着过往船只,突然灵光一闪,两个虚数不够,那就再多加一个!他立刻在桥边石碑上洋洋洒洒刻上几行大字,四元数就此诞生!

z = a + b·i + c·j + d·k
i ² = j ² = k ² = i·j·k = -1
===============================片段分割线===============================
二、如何理解四元数映射到三维空间?
那么为什么是四元数呢,该如何理解四元数呢?我们注意它的唯一约束:
i ² = j ² = k ² = i·j·k = -1
如何理解这组约束呢?一开始我不理解四元数的时候,只有死记硬背这 i·j·k = -1 ,前三个i ² = j ² = k ² = -1 这部分会被当成原来的虚数的概念去理解记忆。但其实四元数的关键就在于 ijk 如何通过 -1 与 i ² = j ² = k ²相关联
因为 i·j·k = -1,两边左乘一个 i,得 i ² ·j·k = -i,即-1·j·k = -i,即 j·k = i
同理可推:
i · j = k ,两边左乘 i,推得 -j = i · k
j · k = i ,两边左乘 j,推得 -k = j · i
k · i = j ,两边左乘 k,推得 -i = k · j
上面的这些推导公式说明什么?暂时不能说明什么,因为还需要“上帝”来指引我们
e^ i·π = -1
没错,就是欧拉恒等式,它代表什么?它所表达的意思就是:如果我们在一个数字上乘以-1,实际上把这个数字在实轴上旋转了180°(想想实轴上的数字1,旋转π后,是不是停留在-1的位置上)那么如果不是旋转180°呢?那也没问题,把公式中的π换成θ,就可以得出数学历史上最著名的欧拉公式。
e^ i·θ = cos(θ) + i sin(θ)
欧拉公式很好的应用于二维平面上的旋转,那自然就会有人想:有没有可能用欧拉公式来表示三维空间的旋转呢?那么就要思考,在三维空间里的虚数是什么样子的?如果能找到一个三维空间的虚数,再应用于欧拉公式上不就可以了?
欸!三维虚数,是不是四元数里的三个虚部?还真没错,三维空间里的虚数 I₃ 如下表示:
I₃ = a·i + b·j + c·k
三维欧拉公式
e^ i·θ = cos(θ) + sin(θ)·( a·i + b·j + c·k)
i ² = j ² = k ² = i·j·k = -1
其中三维虚数还是满足 i ² = j ² = k ² = i·j·k = -1 这一组约束,也就是满足i · j = k那一组推导公式。三维虚数可以直接用三维的xyz坐标系去一一对应。那和原来的三维坐标系欧拉角又有什么不一样呢?关键来了:当上述约束的ijk映射三维坐标系的xyz轴,那么整个坐标系就自带旋转的属性了。如何理解这话?因为虚数的乘法对应几何就是旋转!秘密就在于上面(i · j = k)那六个推导公式。如下图所示,j 沿着 i 逆时针旋转90°就是 -k 了,即 j · i = -k,此时终于搞清楚了上述约束&推导式的伟大之处!


那如果不是90°的旋转呢?套用欧拉公式呗。比如现在要单位矢量 j 在ij轴所构成的平面上,沿着k轴旋转,如下图所示。那我们就可以利用欧拉公式:j · e^ k·θ

j · e^ k·θ
= j · (cos(θ) + k · sin(θ))
= cos(θ) · j + sin(θ) · i
我们继续深入,上面的举例还是简单,因为旋转的只是一个单一的单位方向向量,正常情况都是三维表示法,也就是上面的 j 替换成 (i+j+k) 那会怎样呢?
(i+j+k) · e^ k·θ
= (i+j+k) · (cos(θ) + k · sin(θ))
= i·cos(θ) + i·k·sin(θ) + j·cos(θ) + j·k·sin(θ) + k·cons(θ) + k·k·sin(θ)
= (cos(θ)+sin(θ))·i + (cos(θ)-sin(θ))·j + cos(θ)·k - sin(θ)
注意运算的结果,出现了一项不带任何维度矢量的实数项,我比较菜,不理解这一项的关键点,但是在那些大数学家看来,这是一个非常危险的项啊!想想在一个三维空间上多出了一项值,它并不在这三维空间上的任意维度上,那它表示什么,第四维?暂时按下不表,接着往下。
===============================片段分割线===============================
三、几何层面的四元数。
经过上一节的概述,我们可以理解到四元数的性质非常有利于表达三维空间的旋转,所以了解四元数的性质要先于了解四元数在旋转中的应用。所以前两节的内容主要是阐述复数与四元数之间的关系,在深入探讨四元数的内核前,我觉得有必要先搞明白以下几个比较抽象的概念。
- 空间中的子空间:一般而言,空间(维度>2)都存在更低维的子空间,比如二维空间中一维子空间,也就是直线;三维空间中的一维子空间和二维子空间,也就是直线和面。当超过三维的概念我们就很难去想象是什么样子,但四维空间一定会存在三维子空间或二维子空间。我们这里会加一个前缀超(hyper)来形容这些空间,比如高维空间中的平面我们称为超平面。
- 空间和子空间的映射:我们将二维空间表示为(x,y),当y=0时,其实可以看成是一维的,只不过它表示成(x,0)这种形式。推到四维,(w,x,y,z),当w=0时,(0,x,y,z)就是一个三维子空间,这也是为什么我们可以用单位四元数对三维向量进行操作,其实我们是将三维向量映射到四维的三维子空间(w=0,这种形式也成纯四元数),然后对其进行旋转,最终得到的向量结果依然是这个三维子空间中的,因而可以映射回三维空间。
- 广义球:这里的球是广义上的。我们在二维平面上,广义球其实指代circle,三维空间上就是我们认知上的球,称为two-sphere,而四维空间中广义球其实是一个超球(hyper-sphere),又称为three-sphere。
- 约束与特征向量:空间中的一点由x, y, z等参数来表示,一般来说参数的数量与维数相等,二维空间的点用{x, y}参数,四维空间的点用{x, y, z, w}参数。但是对于空间的点加以约束,则该会减少参数的数量,比如三维空间的点在某一单位球面上,原本三个参数{x, y, z}才能表达的点现在只需要两个参数{u, v}就可以表达。如果{u, v}是单位向量,也可以称{u, v}是{x, y, z}的特征向量。
上述概念给了大家一个思路,四元数这样一个东西并不是一蹴而就的,从空间来说,它与我们熟知的低维空间本质上是没有区别的,或者说是有很大共性的。四元数的很多特性都是从低维拓展而来的,更具体的说是从复数这一概念拓展的。
结合第二节内容,现在可以归纳总结出以下四元数的特性:
- 单位四元数是四维空间中一个超球上面的点,满足w²+x²+y²+z²=1;而纯四元数是四维空间在w=0时的一个子空间的点,形式为{0, q},特别注意的是纯四元数与四元数是不同的概念。再展开来说:
1.1:单位四元数(Unit Quaternion)是一个四元数,其模(或称为范数)等于1。四元数通常用于表示三维空间中的旋转角度,它可以避免万向锁问题,并且能提供平滑的插值方法。
1.2:纯四元数(Pure Quaternion)是四元数的一个子集,它的实部为0,即其一般形式可以表示为 Q = 0 + xi + yj + zk = {0, q},其中 x、y、z 是实数,而 i、j、k 是四元数的虚部单位。纯四元数在几何上可以被视为三维空间中的向量,其中 x、y、z 分别代表向量的三个分量。 - 四元数是复数虚部扩展的结果,复数的虚部为1个,而四元数虚部有3个,且两两互相正交,其中实部是cosθ/2,而虚部为一个単位轴乘以sinθ/2。
- 四元数自由度并没有四个维度,由于存在w²+x²+y²+z²=1这个约束,它的自由度其实只有3,且每个四元数可以对应一个特征向量,即n。但请记住四元数并不是与特征向量一一对应的,后文会有说。
这里先举个例子,三维的球用代数表示为x²+y²+z²=1,虽然球上面的点是由x,y,z三个参数来确定,但实际上我们只需要两个。假设取x和z表示,其中y可以通过x和z进行求解。那么,我们将y轴信息给隐去,只看投影平面,如下图所示。这张图的意思是,整个球在XOZ平面上投影是一个圆,当球面一点投影在圆上时,y=0;投影的位置位于圆内时,则分别两种情况,y>0处于北半球,y<0处于南半球。所以我们仅通过投影后的圆即可还原出整个球体。
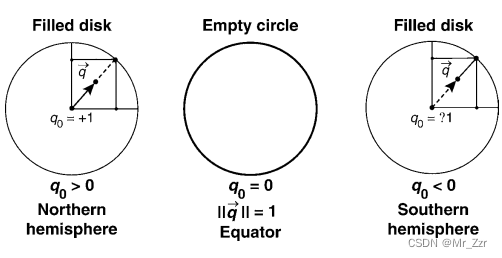
让我们推广到四维,w²+x²+y²+z²=1中取x、y和z来表示超球。如下图所示,四维空间投影到三维超平面(w=0)可能是一个two-sphere。当投影点在整个two-sphere的边缘时,w一定为0,值得一提的是在这个空间内的四元数是一个纯四元数。当投影点落在two-sphere的内部时,也分为两种情况,w>0和w<0。但是我们可以发现这两种情况下对应的特征向量是一样的,所以我们将旋转矩阵向四元数转换时,是有两个对应值的,四元数的范围是2倍覆盖于3D旋转(2:1 mapping)。上面写的相对来说比较隐晦,但我觉得可以对理解四维空间和四元数相当有帮助。本文表述能力有限,如果实在看不懂的,可以翻阅《Visualizing Quaternions》第八章,个人觉得这是书中最为精彩的部分之一。
现在回头看第二节最后例子,我们甚至可以推广到任意三维向量绕任意轴进行旋转的基本通式:
三维任意向量:Q = 0 + xi + yj + zk = {0, q}
旋转轴:P = w + xi + yj + zk = {s, p}
即: {0, q} · e^{s, p}θ
但此时发现,三维虚数版本的欧拉公式适应不了单位四元数的运算,那要如何处理呢?请看下一篇详细探讨四元数的乘法。