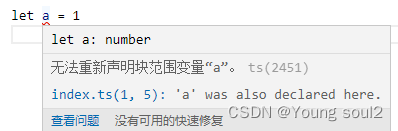
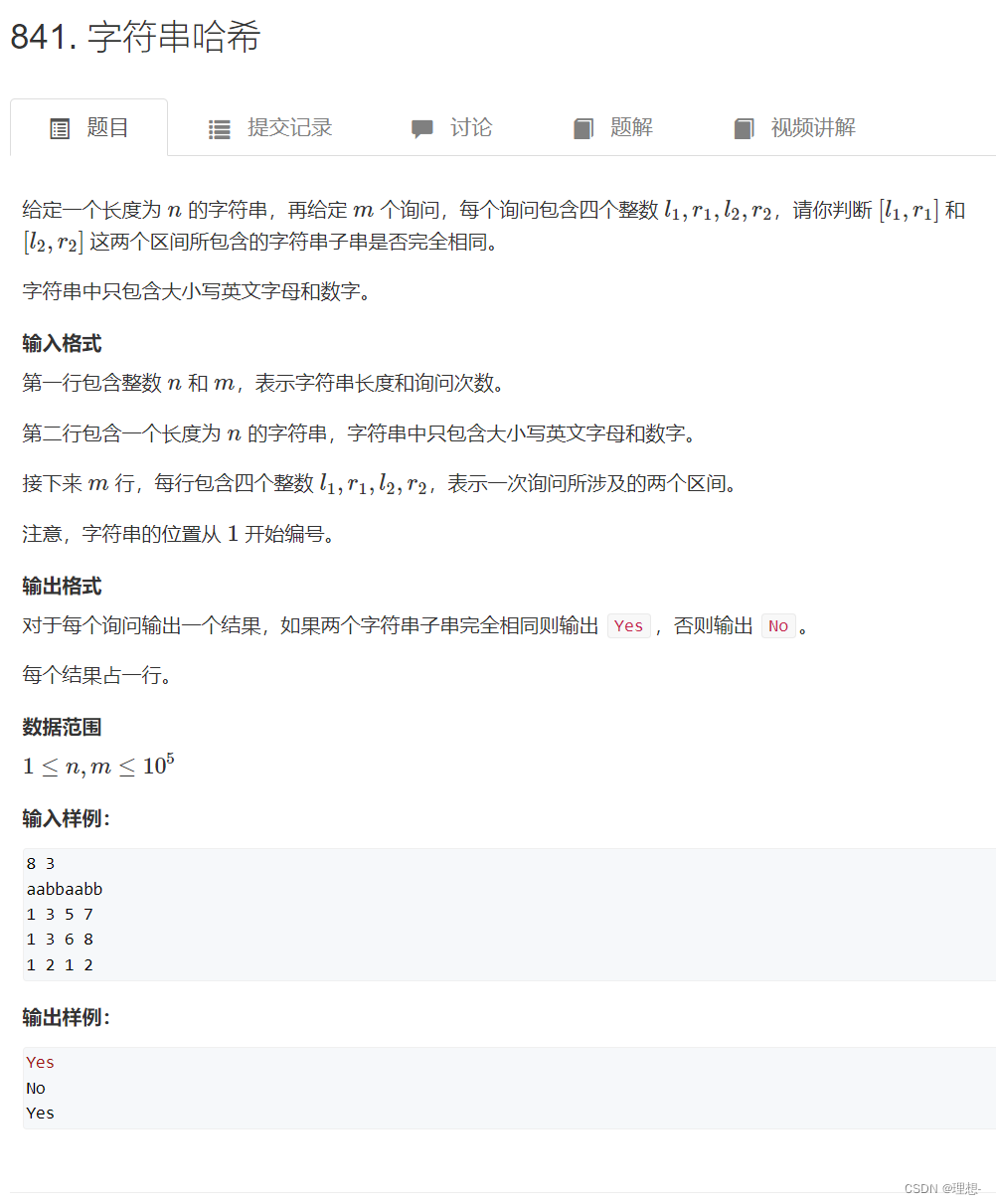
题面如下：

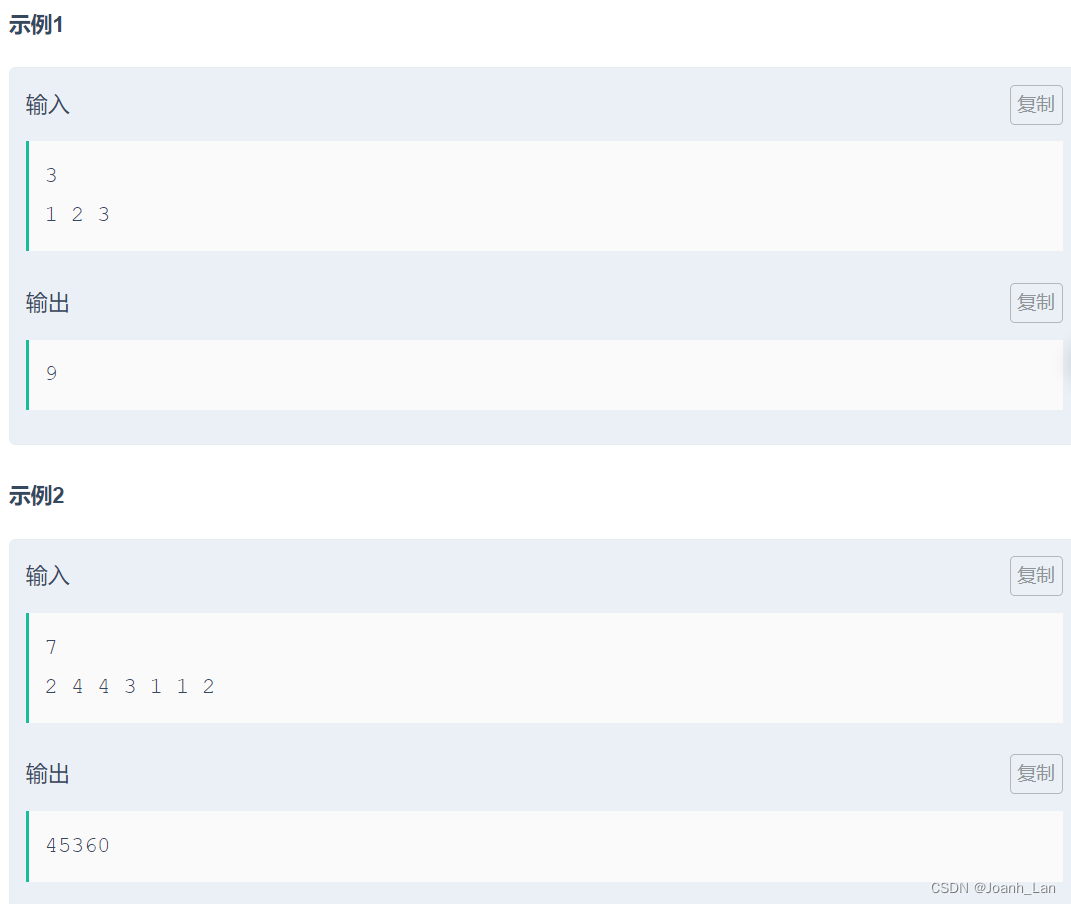
思路 or 题解：

对于一个长度为 $n$ 的 排列组合
如果存在一对 逆序对 $(x,y)$
$x$ 在 $y$ 的前面有 $\frac{n\ast (n-1)}{2}$ 种情况
剩下 $n-2$ 个位置可以随意填数进去，不会影响到逆序对 $(x,y)$

所以答案是：
$(n-2)!\times \frac{n\ast (n-1)}{2}\times 逆序对的个数$

AC代码如下：

const int mod = 1e9 + 7;
const int N = 100009;
int n, s[N];
int sum[N];
int ksm(int a, int b)
{
    int res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}
void solve()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> s[i];
        sum[s[i]]++;
    }
    for (int i = 1; i <= 100000; i++)
        sum[i] += sum[i - 1];
    
    int num = 0;
    for (int i = 100000; i >= 1; i--)
    {
        num = (num + ((sum[i] - sum[i - 1]) * sum[i - 1]) % mod) % mod;
    }

    int ans = 1;
    for (int i = 1; i <= n - 2; i++)
        ans = ans * i % mod;
    ans = ans * num % mod;
    ans = ((ans * n) % mod * (n - 1)) % mod;
    ans = ans * ksm(2, mod - 2) % mod;
    cout << ans << '\n';
}
signed main()
{
    buff;
    solve();
}