AcWing 数据结构

news2025/7/28 5:57:42

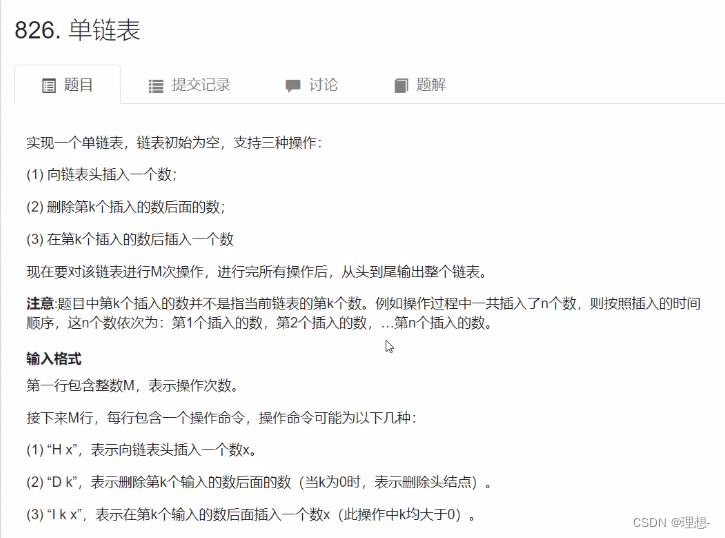
单链表

邻接表用的多 存储树和图 new()速度慢 数组模拟

模板

-1代表头节点

const int N = 1e6 + 5;
// head存储链表头
//e[]存储节点的值
//ne[]存储节点的next指针
//idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 将a插到链表头
void add_to_head(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;
}

//将x插入到下标是k的点的后面
void add(int k, int x)
{
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx++;
}

//将下标是k的点后面的点删掉
void remove(int k)
{
    ne[k] = ne[ne[k]];
}


// 将头结点删除，需要保证头结点存在
void remove()
{
    head = ne[head];
}

0代表头节点

const int N = 100010;
// 0表示头节点 使得所有节点操作一致 不用考虑是否为头节点或尾结点
// ne[0] 表示第一个节点
int e[N], ne[N], idx = 1;

void insert(int k, int x)
{
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}

void remove(int k, int x)
{
    ne[k] = ne[ne[k]];
}

单链表

在这里插入图片描述

代码

-1代表头节点

#include<iostream>
using namespace std;
const int N = 100010;
int head, e[N], ne[N], idx;
void init()
{
    head = -1;
    idx = 0;
}
//头插
void add_to_head(int x)
{
    e[idx] = x;
    ne[idx] = head;
    head = idx++;
}
void remove(int k)
{
    ne[k] = ne[ne[k]];
}
void insert(int k, int x)
{
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}
int main()
{
    int m;
    cin >> m;
    init();
    while (m--)
    {
        char op;
        int k, x;
        cin >> op;
        if (op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if (op == 'D')
        {
            cin >> k;
            if (!k) head = ne[head];
            else remove(k - 1);
        }
        else 
        {
            cin >> k >> x;
            insert(k - 1, x);
        }
    }
    for (int i = head; i != - 1; i = ne[i]) cout << e[i] << ' ';
    
    return 0;
}

0代表头节点

即使是一个字符 也建议用数组来存 忽略空格换行的影响

#include<iostream>
using namespace std;

const int N = 100010;
// 0表示头节点 使得所有节点操作一致 不用考虑是否为头节点或尾结点
// ne[0] 表示第一个节点
int e[N], ne[N], idx = 1;

void insert(int k, int x)
{
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}

void remove(int k)
{
    ne[k] = ne[ne[k]];
}

int main()
{
    int m;
    scanf("%d", &m);
    //即使是一个字符 也建议用数组来存 忽略空格换行的影响
    char op[2];
    int k, x;
    
    while (m--)
    {
        scanf("%s", op);
        if (op[0] == 'H')
        {
            scanf("%d", &x);
            insert(0, x);
        }
        else if (op[0] == 'D')
        {
            scanf("%d", &k);
            remove(k);
        }
        else 
        {
            scanf("%d%d", &k, &x);
            insert(k, x);
        }
    }
    
    for (int i = ne[0]; i != 0; i = ne[i]) printf("%d ", e[i]);
    
    return 0;
}

双链表

模板

const int N = 100010;
int e[N], l[N], r[N], idx;

// 初始化 0头节点 1尾节点
void init()
{
    r[0] = 1, l[1] = 0, idx = 2;
}

// 下标是k的右边插入一个
void add(int k, x)
{
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx;
    r[k] = idx++;
}

//删除第k个
void remove(int k)
{
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

在这里插入图片描述

  1. 之所以在 “D”, “IL”, “IR” 要用 k+1 的原因是 双链表的起始点是2. 所以，每个插入位置k的真实位置应该为 k-1+2 = k+1 (在单链表中为 k-1)。
  2. 0, 1 节点的作用是边界。0为左边界，1为右边界。他俩在这里有点类似保留字的作用。正因如此，我们的idx也是从2开始
  3. 最后遍历输出结果的 for (int i = r[0]; i != 1; i = r[i])。从r[0]开始是因为 0 为左边界，而终止条件 i==1是因为1为右边界（如果碰到，说明已经遍历完毕）

代码

#include<iostream>
using namespace std;
const int N = 100005;
int idx, e[N], l[N], r[N];
void insert(int k, int x)
{
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx++;
}
void remove(int k)
{
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}
int main()
{
    r[0] = 1, l[1] = 0, idx = 2;
    cin >> m;
    while (m--)
    {
        string op;
        int k, x;
        cin >> op;
        if (op == "L") cin >> x, insert(0, x);
        else if (op == "R") cin >> x, insert(l[1], x);
        else if (op == "D") cin >> k, remove(k + 1);
        else if (op == "IL") cin >> k >> x, insert(l[k + 1], x);
        else cin >> k >> x, insert(k + 1, x);
    }
    for (int i = r[0]; i != 1; i = r[i])
        cout << e[i] << ' ';
    return 0;
}

栈

模板

// tt表示栈顶
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0) not empty
{

}

模拟栈

在这里插入图片描述

代码

#include<iostream>
using namespace std;
const int N = 100010;
int top, stk[N];

int main()
{
    string op;
    int m, x;
    cin >> m;
    while (m--)
    {
        cin >> op;
        if (op == "push") cin >> x, stk[++top] = x;
        else if (op == "pop") top--;
        else if (op == "empty") cout << (top > 0 ? "NO" : "YES") << endl;
        else cout << stk[top] << endl;
    }
    return 0;
}

表达式求值

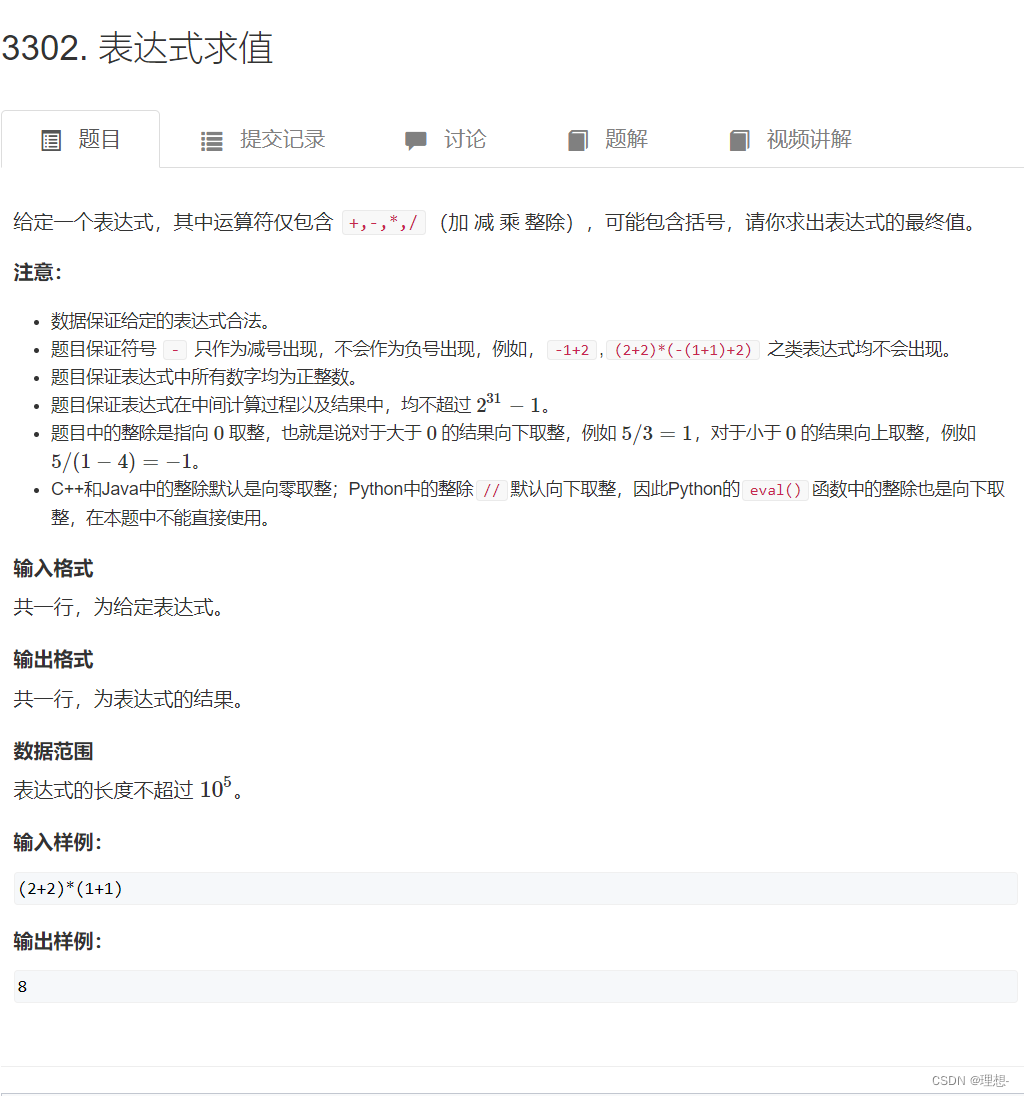
在这里插入图片描述

代码

队列

普通队列

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt) not empty
{

}

循环队列

模拟队列

在这里插入图片描述

#include<iostream>
using namespace std;

const int N = 100010;
int hh, tt = -1, q[N];

int main()
{
    int m, x;
    string op;
    cin >> m;
    while (m--)
    {
        cin >> op;
        if (op == "push") cin >> x, q[++tt] = x;
        else if (op == "pop") hh++;
        else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
        else cout << q[hh] << endl;
    }
    return 0;
}

单调栈

模板

常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

AcWing 830. 单调栈

在这里插入图片描述

#include<iostream>
using namespace std;

const int N = 100010;
int top, stk[N], n, a[N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0; i < n; i++)
    {
        while (top && stk[top] >= a[i]) top--;
        if (top) cout << stk[top] << ' ';
        else cout << -1 << ' ';
        stk[++top] = a[i];
    }
    return 0;
}

单调队列

模板

常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

154.滑动窗口

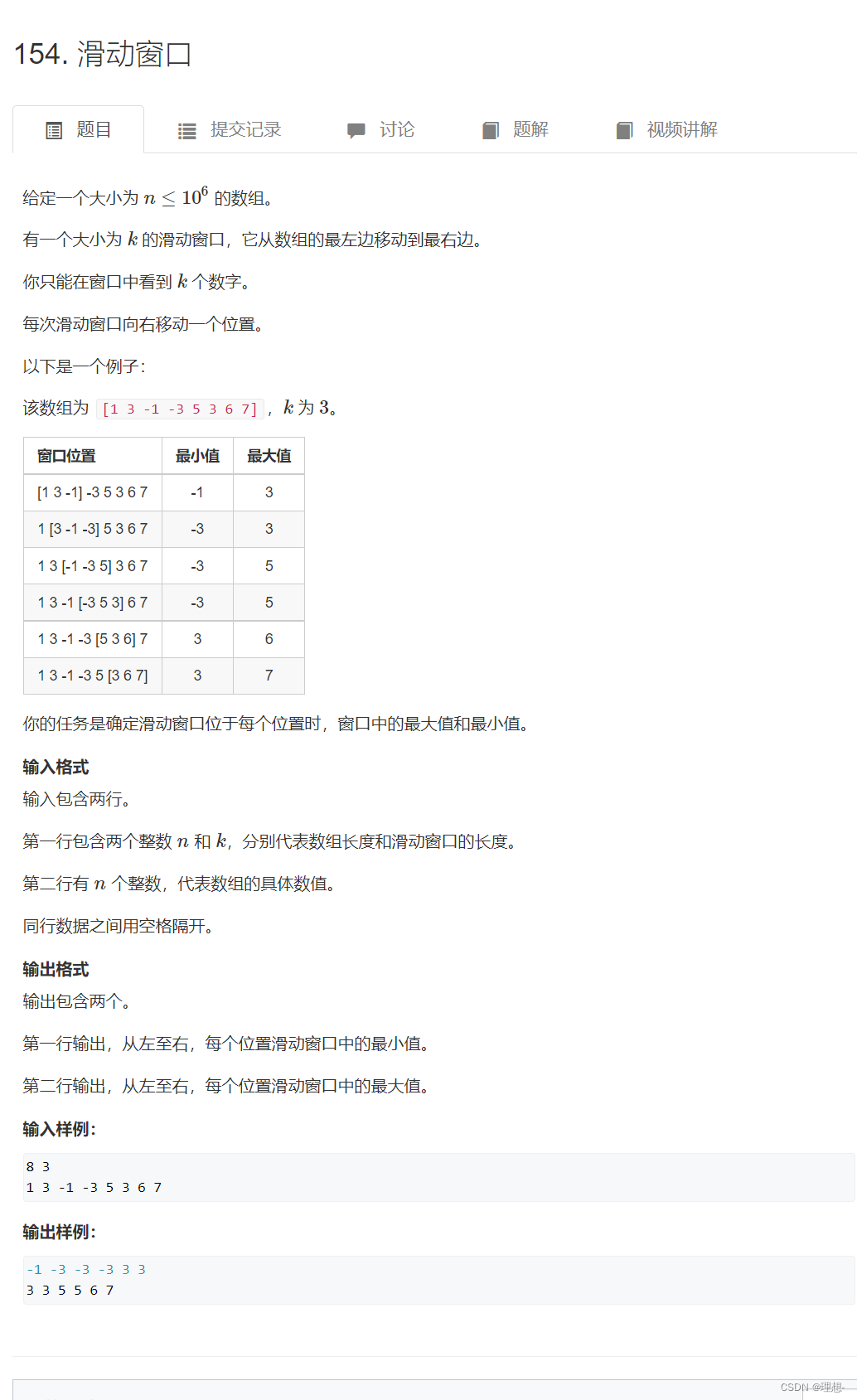
在这里插入图片描述

#include<iostream>
using namespace std;
const int N = 1000010;
int a[N], q[N], n, k;
int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    int hh = 0, tt = -1;
    for (int i = 0; i < n; i++)
    {
        // 判断队头是否滑出窗口, 队列存储下标
        if (hh <= tt && i - k + 1 > q[hh]) hh++;
        // 比当前元素大的时候 往前遍历
        while (hh <= tt && a[q[tt]] >= a[i]) tt--;
        // 在队尾加入当前元素
        q[++tt] = i;
        // 第k个数及以后才输出
        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }
    printf("\n");
    hh = 0, tt = -1;
    for (int i = 0; i < n; i++)
    {
        // 判断队头是否滑出窗口, 队列存储下标
        if (hh <= tt && i - k + 1 > q[hh]) hh++;
        // 比当前元素大的时候 往前遍历
        while (hh <= tt && a[q[tt]] <= a[i]) tt--;
        // 在队尾加入当前元素
        q[++tt] = i;
        // 第k个数及以后才输出
        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }
    return 0;
}

KMP

模板

// s[]是长文本，p[]是模式串，短串，n是s的长度，m是p的长度
求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // 匹配成功后的逻辑
    }
}

在这里插入图片描述

#include<iostream>
using namespace std;
const int N = 100010, M = 1000010;
int ne[N];
char p[N], s[M];
int n, m;
int main()
{
    cin >> n >> p + 1 >> m >> s + 1;
    for (int i = 2, j = 0; i <= n; i++)
    {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j++;
        ne[i] = j;
    }
    for (int i = 1, j = 0; i <= m; i++)
    {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j++;
        if (j == n)
        {
            printf("%d ", i - n);
            j = ne[j];
        }
    }
    return 0;
}

Trie树

高效地存储和查找字符串集合的数据结构

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QIWq9VYh-1668740282430)(%E7%AC%AC%E4%BA%8C%E7%AB%A0%20%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84.assets/image-20221104145837283.png)]

Trie字符串统计

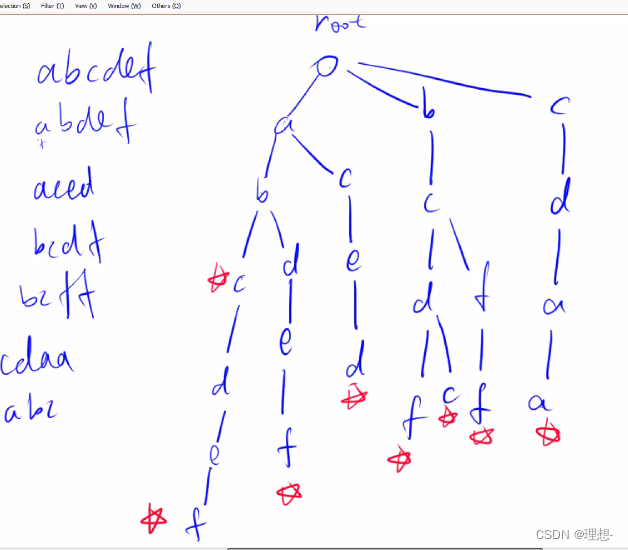
在这里插入图片描述

代码:

#include<iostream>
using namespace std;
const int N = 100010;
int son[N][26], cnt[N], idx; // 下标是0的点 既是根节点又是空节点
char str[N];
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
    cnt[p]++;
}
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}
int main()
{
    int n;
    scanf("%d", &n);
    while (n--)
    {
        char op[2];
        scanf("%s%s", op, str);
        if (op[0] == 'I') insert(str);
        else printf("%d\n", query(str));
    }
    return 0;
}

最大异或对

在这里插入图片描述

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 100010, M = 31 * N;

int a[N], son[M][2]; 
int n, idx;

void insert(int x)
{
    int p = 0; // 
    for (int i = 31; i >= 0; i--)
    {
        int u = x >> i & 1; // 取二进制数的某一位的值
        if (!son[p][u]) son[p][u] = ++idx; // 如果下标为p的点的u（0或1）这个儿子不存在，那就创建
        p = son[p][u];
    }
}

int query(int x)
{
    int p = 0, ret = 0;
    for (int i = 31; i >= 0; i--)
    {
        int u = x >> i & 1;
        if (son[p][!u])
        {
            p = son[p][!u];
            ret = ret * 2 + !u; 
        }
        else
        {
            p = son[p][u];
            ret = ret * 2 + u;
        }
    }
    return ret;
}

int main()
{
    cin >> n;
    int res = 0; 
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &a[i]);
        insert(a[i]);
        int t = query(a[i]);
        res = max(res, t ^ a[i]);
    }

    cout << res << endl;

    return 0;
}

并查集

合并集合

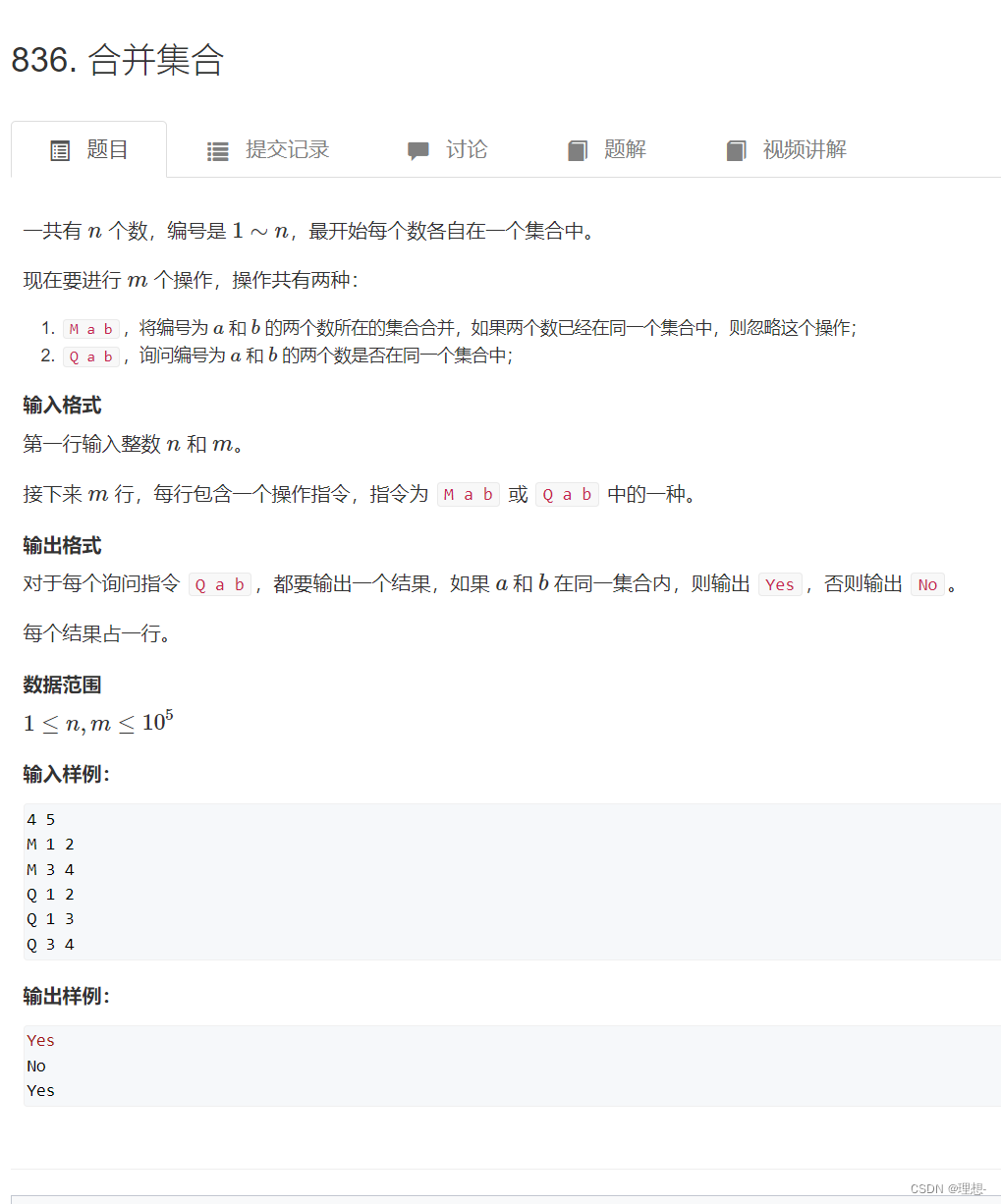
在这里插入图片描述

模板

#include<iostream>
using namespace std;
const int N = 100010;
int n, m;
int p[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) p[i] = i;
    while (m--)
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        
        if (op[0] == 'M') p[find(a)] = p[find(b)];
        else 
        {
            if (find(a) == find(b)) puts("YES");
            else puts("NO");
        }
    }
    return 0;
}

连通块中点的数量

在这里插入图片描述

#include<iostream>
using namespace std;

const int N = 100010;
// p[N]维护祖宗节点 cnt[N]维护集合的元素个数
int p[N], cnt[N], n, m;

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void con(int a, int b)
{
    if (find(a) == find(b)) return;
    //不在一个集合才合并数量
    else 
    {
        cnt[find(b)] = cnt[find(a)] + cnt[find(b)];
        p[find(a)] = find(b);
    }
}

int main()
{
    int a, b;
    char op[5];
    cin >> n >> m;
    for (int i = 1; i <= n; i++) p[i] = i, cnt[i] = 1;
    while (m--)
    {
        scanf("%s", op);
        if (op[0] == 'C') 
        {
            scanf("%d%d", &a, &b);
            con(a, b);
        }
        else if (op[1] == '1') 
        {
            scanf("%d%d", &a, &b);
            printf(find(a) == find(b) ? "Yes\n" : "No\n");
        }
        else 
        {
            scanf("%d", &a);
            printf("%d\n", cnt[find(a)]);
        }
    }
    return 0;
}

堆

基本概念：一棵完全二叉树

  • 小根堆
  • 大根堆

基本操作

  • 插入一个数
  • 求集合中的最小值
  • 删除最小值
  • 删除任意一个元素
  • 修改任意一个元素
    在这里插入图片描述

模板

// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
void heap_swap(int a, int b)
{
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

// 向下调整，大的元素放下面
void down(int i)
{
    int t = i;
    // i与左右节点最小值交换 （如果存在的话）
    if (i * 2 <= len && h[i * 2] < h[t]) t = i * 2;
    if (i * 2 + 1 <= len && h[i * 2 + 1] < h[t]) t = i * 2 + 1;
    if (i != t)
    {
        heap_swap(i, t);
        down(t);
    }
}

//向上调整，小的元素放上面
void up(int i)
{
    while (i / 2 && h[i] < h[i / 2])
    {
        heap_swap(i, i / 2);
        i /= 2;
    }
}

// 初始化堆 O(n)的复杂度
for (int i = n / 2; i; i--) down(i);

堆排序

在这里插入图片描述

#include<iostream>
using namespace std;

const int N = 100010;
int h[N], n, m, len;

void down(int i)
{
    int t = i;
    // i与左右节点最小值交换 （如果存在的话）
    if (i * 2 <= len && h[i * 2] < h[t]) t = i * 2;
    if (i * 2 + 1 <= len && h[i * 2 + 1] < h[t]) t = i * 2 + 1;
    if (i != t)
    {
        swap(h[i], h[t]);
        down(t);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    
    for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
    len = n;
    
    // 初始化堆 O(n)的复杂度
    for (int i = n / 2; i; i--) down(i);
    
    while (m--)
    {
        printf("%d ", h[1]);
        h[1] = h[len];
        len--;
        down(1);
    }
    
    return 0;
}

模拟堆

#include<iostream>
using namespace std;

const int N = 100010;
int h[N], hp[N], ph[N], n, m, len;

void heap_swap(int a, int b)
{
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int i)
{
    int t = i;
    // i与左右节点最小值交换 （如果存在的话）
    if (i * 2 <= len && h[i * 2] < h[t]) t = i * 2;
    if (i * 2 + 1 <= len && h[i * 2 + 1] < h[t]) t = i * 2 + 1;
    if (i != t)
    {
        heap_swap(i, t);
        down(t);
    }
}

void up(int i)
{
    while (i / 2 && h[i] < h[i / 2])
    {
        heap_swap(i, i / 2);
        i /= 2;
    }
}

int main()
{
    scanf("%d", &n);
    string op;
    int k, x;
    
    while (n--)
    {
        cin >> op;
        if (op == "I") 
        {
            scanf("%d", &x);
            len++;
            m++;
            ph[m] = len, hp[len] = m;
            h[len] = x;
            up(len);
        }
        else if (op == "PM") printf("%d\n", h[1]);
        else if (op == "DM")
        {
            heap_swap(1, len);
            len--;
            down(1);
        }
        else if (op == "D")
        {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, len);
            len--;
            down(k), up(k);
        }
        else
        {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            down(k), up(k);
        }
    }
    
    return 0;
}

Hash表

模板

//(1) 拉链法
int h[N], e[N], ne[N], idx;

// 向哈希表中插入一个数
void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++ ;
}

// 在哈希表中查询某个数是否存在
bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x)
            return true;

    return false;
}

//(2) 开放寻址法
int h[N];

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x)
    {
        t ++ ;
        if (t == N) t = 0;
    }
    return t;
}

模拟散列表

在这里插入图片描述

拉链法

#include<iostream>
#include <cstring>
using namespace std;

const int N = 100003;
int h[N], e[N], ne[N], idx;
int n;

void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}

bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x) return true;
        
    return false;
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    char op[2];
    int x;
    while (n--)
    {
        scanf("%s%d", op, &x);
        if (op[0] == 'I') insert(x);
        else printf(find(x) ? "Yes\n" : "No\n");
    }
    return 0;
}

开放寻址法，范围2~3倍

#include<iostream>
#include <cstring>
using namespace std;

const int N = 200003, null = 0x3f3f3f3f; // 范围2~3倍 质数
int h[N];
int n;

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
    int k = (x % N + N) % N;
    
    while (h[k] != null && h[k] != x)
    {
        k++;
        if (k == N) k = 0;
    }
        
    return k;
}

int main()
{
    scanf("%d", &n);
    // memset 按字节赋值 后八位
    memset(h, 0x3f, sizeof h);
    char op[2];
    int x;
    while (n--)
    {
        scanf("%s%d", op, &x);
        int k = find(x);
        if (op[0] == 'I') h[k] = x;
        else printf(h[k] != null  ? "Yes\n" : "No\n");
    }
    return 0;
}

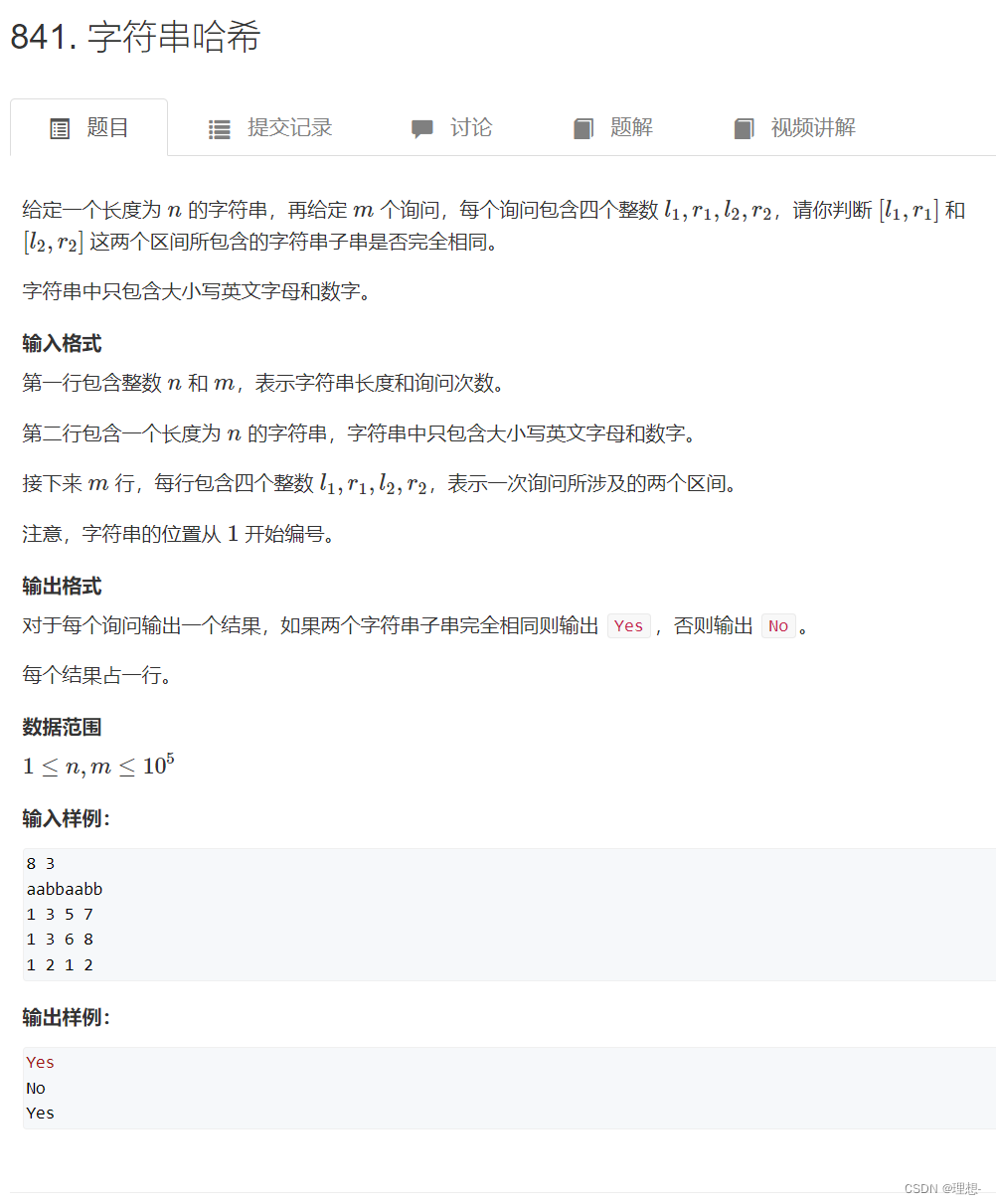
字符串哈希

**核心思想：**将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
**小技巧：**取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果

在这里插入图片描述

在这里插入图片描述

模板

typedef unsigned long long ull;
u h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64

// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
    h[i] = h[i - 1] * P + str[i];
    p[i] = p[i - 1] * P;
}

// 计算子串 str[l ~ r] 的哈希值
ull get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

在这里插入图片描述

代码

#include<iostream>
using namespace std;

typedef unsigned long long ull;

const int N = 100005, P = 131;
ull h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
char str[N];
int n, m;

// 计算子串 str[l ~ r] 的哈希值
ull get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    scanf("%d%d%s", &n, &m, str + 1);
    // 初始化
    p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
    
    while (m--)
    {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if (get(l1, r1) == get(l2, r2)) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/16473.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

皕杰报表之控件元素

皕杰报表之控件元素

在皕杰报表中&#xff0c;填报操作时&#xff0c;控件类型分为无输入控件、文本框、文本域、下拉框、下拉树、单选框、复选框、日期、时间、日期时间、自定义控件类型。如图所示&#xff1a; 1 无输入控件 选中此控件的单元格在页面生成无任何变化&#xff1b; 2 文本框 选中…
阅读更多...
加拿大海运专线怎么选?加拿大海运专线有哪些费用

加拿大海运专线怎么选?加拿大海运专线有哪些费用

由于全球经济的发展&#xff0c;近年来&#xff0c;越来越多的国内跨境电商卖家向加拿大和、墨西哥、欧洲、美国等出口货物&#xff0c;而海运的运输方式相对比较划算。那么加拿大海运专线怎么选?又有哪些费用呢?一、加拿大海运专线怎么选 加拿大海运专线运输方式有整柜运输和…
阅读更多...
Linux-----网络套接字编程

Linux-----网络套接字编程

文章目录铺垫一下概念知识基于UDP协议下的套接字编程基于TCP协议下的套接字编程铺垫一下概念知识 我们知道IP地址是用来标识主机唯一性的。 而源IP地址表示从哪个主机来&#xff0c; 目的IP地址表示去哪个主机。 端口号&#xff08;port&#xff09;&#xff1a; 1&#xff0…
阅读更多...
C++之继承、派生

C++之继承、派生

目录 1.继承的概念与定义 2.层次概念是计算机的重要概念: 3.私有的能被继承&#xff0c;不能被访问 4.继承的三步骤 1.继承语法 2.继承例子 5.有继承和组合的构造顺序---内存布局 6.继承之下的赋值运算符重载 1.基础知识 2.Person、Student例子 7.一个类被多个类继承 …
阅读更多...
22.11.18打卡 [传智杯 #3 初赛] 部分题

22.11.18打卡 [传智杯 #3 初赛] 部分题

森林图论懒得写, 等搞完dp之后再来复习图论, 还有一题数据有问题没写 [传智杯 #3 初赛] 课程报名 - 洛谷 哇真的签到, 第一眼还想着推公式呢, 看这数据范围直接暴力了 /* ⣿⣿⣿⣿⣿⣿⡷⣯⢿⣿⣷⣻⢯⣿⡽⣻⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣇⠸⣿⣿⣆⠹⣿⣿⢾⣟⣯⣿⣿…
阅读更多...
LiveGBS/LiveNVR组合实现GB35114平台端和GB35114设备端的GB35114的交互流程

LiveGBS/LiveNVR组合实现GB35114平台端和GB35114设备端的GB35114的交互流程

概述&#xff1a; GB35114是在GB28181基础上扩展而来&#xff0c;增加了身份认证和数据加密。LiveNVR设备通过GB35114注册到LiveGBS时&#xff0c;LiveGBS平台端需要校验LiveNVR设备的身份&#xff0c;这是单向认证。同时可选LiveNVR也检验LiveGBS平台的身份&#xff0c;如果互…
阅读更多...
[Howto] Pytorch Window GPU 环境配置

[Howto] Pytorch Window GPU 环境配置

注&#xff1a; how to 系列只有基本的操作&#xff0c;不涉及原理&#xff0c;类似于操作手册。 Linux&#xff0c;MacOS和Window配置方法差不多&#xff0c;就是环境变量的修改方式不太一样&#xff0c;就不单独说明了。 1. 确定Pytorch版本 估计像我一样的初学者&#xf…
阅读更多...
关于commonjs、AMD、UMD、ESM以及ts模块之间的使用差异

关于commonjs、AMD、UMD、ESM以及ts模块之间的使用差异

commonjs 特点&#xff1a;一个文件就是一个模块&#xff0c;拥有独立的作用域&#xff0c;适用于服务端不适合浏览器端。导出模块内部数据通过module.exports或exports对象默认导出&#xff1a; // true const a 1 const b 2 module.exports {a, b }或者 // true const …
阅读更多...
【跨境电商卖家】Instagram营销初学者指南（二）：方法与技巧

【跨境电商卖家】Instagram营销初学者指南（二）：方法与技巧

关键词&#xff1a;跨境电商卖家、instagram营销 1.为 Instagram营销设定目标 在你开始在 Instagram 上发帖之前&#xff0c;问问你自己&#xff08;或你的团队&#xff09;一件事&#xff1a;你为什么在 Instagram 上&#xff1f;尽管该平台很受欢迎&#xff0c;但您的回答不…
阅读更多...
linux笔记(6):东山哪吒D1H显示HDMI测试-命令行调试

linux笔记(6):东山哪吒D1H显示HDMI测试-命令行调试

文章目录1.测试流程和结果2.测试过程详解2.1 挂载测试工具1.2 设置参数1.2.1设置name1.2.2选择命令1.2.3 设置命令参数1.3开启显示3.还没搞清楚怎么在应用中显示字符测试开发板的HDMI输出。 参考文档&#xff1a;全志官方文档。 1.测试流程和结果 测试结果&#xff1a; 2.测…
阅读更多...
如何实现一键全选

如何实现一键全选

利用复选框的激活、非激活实现一键全选功能 效果展示 前置准备 投票列表素材 具体步骤 添加素材 制作列表复选框 制作一件全选按钮 创建复选框相关行为触发器 制作一键全选触发器 步骤分解 添加素材 拖拽 图片组件 到 根容器 选中 图片组件 铺满父级容器 点击 检查面板 中的 …
阅读更多...
一种新的群体智能优化算法：麻雀搜索算法（SSA）（Matlab代码实现）

一种新的群体智能优化算法：麻雀搜索算法（SSA）（Matlab代码实现）

&#x1f352;&#x1f352;&#x1f352;欢迎关注&#x1f308;&#x1f308;&#x1f308; &#x1f4dd;个人主页&#xff1a;我爱Matlab &#x1f44d;点赞➕评论➕收藏 养成习惯&#xff08;一键三连&#xff09;&#x1f33b;&#x1f33b;&#x1f33b; &#x1f34c;希…
阅读更多...
C++中函数调用的整个过程内存堆栈分配详解

C++中函数调用的整个过程内存堆栈分配详解

函数调用过程中&#xff1a;实参将值拷贝给函数的形参&#xff0c;而函数的形参相当于一个生存周期位于函数 内部的局部变量&#xff0c;函数内部的内存操作也只是将拷贝到形参的值进行操作&#xff0c;形参在函数结束 后会被栈自动回收释放(形参在栈中分配)&#xff0c;这就是…
阅读更多...
Spring Security如何防止会话固定攻击

Spring Security如何防止会话固定攻击

在春季安全课程的这篇文章中&#xff0c;我们将研究春季安全会话固定以及如何防止春季应用程序中的会话劫持。 春季安全会话固定 会话固定是一种非常常见且最常见的攻击类型&#xff0c;恶意攻击者可以通过访问站点来创建会话&#xff0c;然后诱使其他用户使用相同的会话登录…
阅读更多...
副业是刚需？分享几个程序员接外包私活的网站

副业是刚需？分享几个程序员接外包私活的网站

经常看到某某程序员接了个项目开发&#xff0c;工作之余轻轻松松赚了钱还顺带提升了技术&#xff1b;或者看到某大佬又发表了一篇程序员技术提升稿件&#xff0c;阅读点赞收藏三连发&#xff0c;这个月的零花钱又不愁了...但自己只是一名普普通通的程序员&#xff0c;能找到这样…
阅读更多...
Golang入门笔记（10）—— 闭包 closure

Golang入门笔记（10）—— 闭包 closure

先看一段代码&#xff0c;脱离代码讲闭包&#xff0c;太干了。 package mainimport "fmt"func main() {a : Adder()fmt.Println(a(1))fmt.Println(a(2))fmt.Println(a(3)) }func Adder() func(int) int { // 累加器&#xff1a;这里从10开始累加var sum int 10retu…
阅读更多...
linux时区相关

linux时区相关

背景&#xff1a;用linux自带的时间接口函数读取时间的时候&#xff0c;发现有时候时间与北京时间不符合&#xff0c;经过研究发现&#xff1a;时间 UTC时间时区带来的偏移。操作方法&#xff1a;timedatectl list-timezones可看支持的时区改时区方法有如下两种&#xff1a; l…
阅读更多...
【LeetCode 每日一题】15. 三数之和

【LeetCode 每日一题】15. 三数之和

01 题目描述 给你一个整数数组 nums &#xff0c;判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k &#xff0c;同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意&#xff1a;答案中不可以包含重复的三元…
阅读更多...
【数据结构】链表LinkedList

【数据结构】链表LinkedList

1.ArrayList的缺陷 2.单链表的实现 3.LinkedList的使用&#xff08;模拟实现&#xff09; 我们之前介绍过ArrayList了&#xff0c;它的底层是数组&#xff0c;数组是一段连续的空间&#xff0c;当我们想要插入或者删除数据的时候&#xff0c;插入元素&#xff0c;就要让插入位置…
阅读更多...
用树莓派PICO做一个桌面时钟超详细教程！

用树莓派PICO做一个桌面时钟超详细教程！

用树莓派PICO做一个可显示时间和温湿度的桌面时钟一、概述二、材料准备1、树莓派PICO2、DHT11温湿度传感器3、DS1302时钟模块&#xff08;选用&#xff09;4、SSD1306屏幕5、其他材料三、开始1、连线2、写程序&#xff08;1&#xff09;使用内置RTC函数实现的时钟&#xff08;2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023