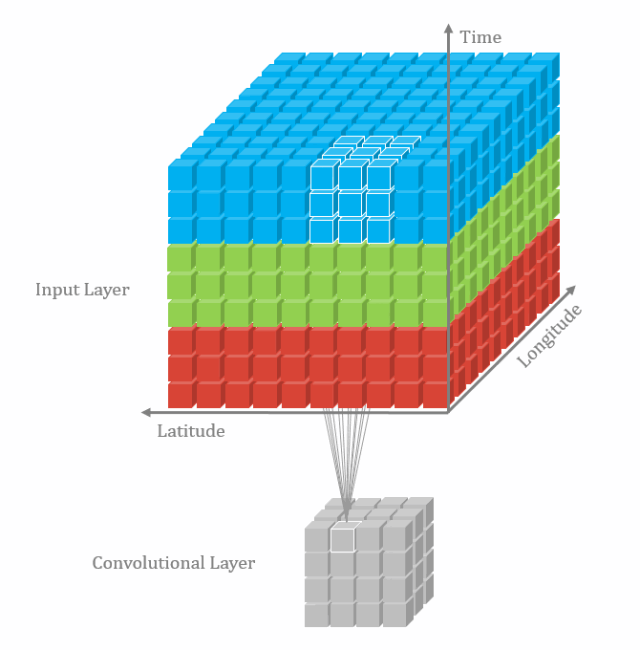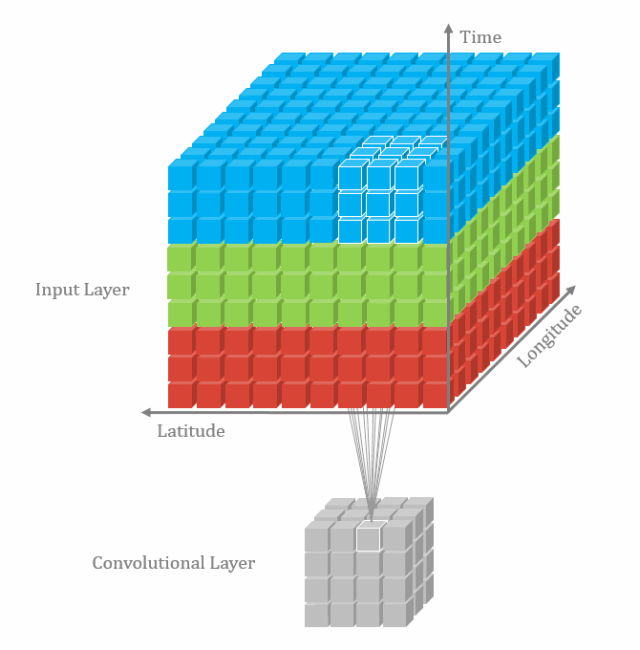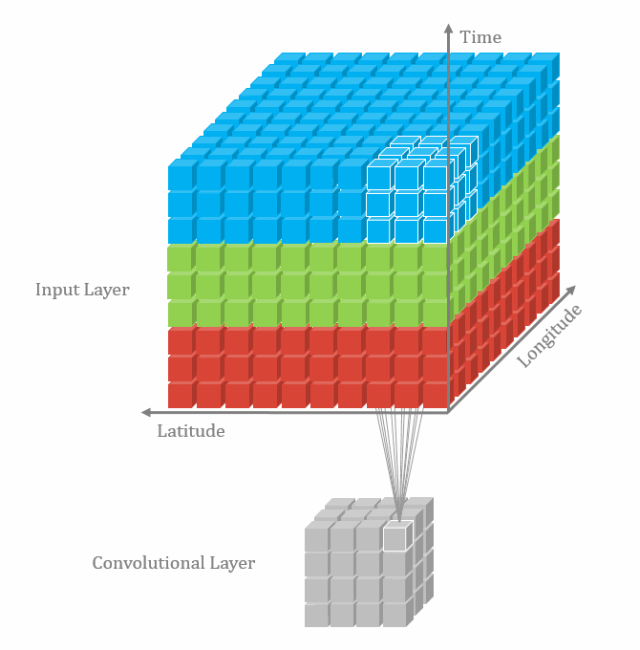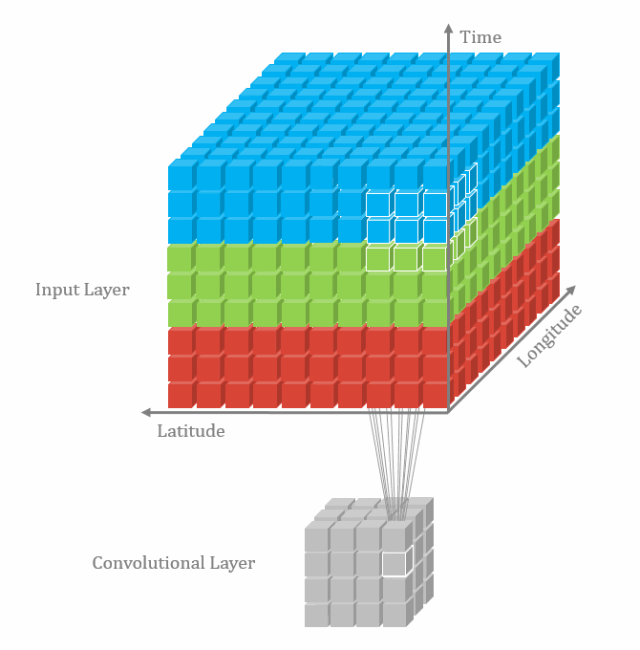
核心思想
该文提出一种基于局部保持的特征匹配方法(LPM)。其核心思想是对于一个正确匹配点,其邻域范围内的其他匹配点与对应目标点之间的变换关系,应该和正确的匹配点保持一致,而错误匹配点,则应该有较大的差别。基于这一假设前提,作者采用KNN算法为每个特征点构建邻域范围,并设计了一个损失函数来计算候选匹配点集中各个匹配对之间的距离损失,差异越大则损失越大。然后,考虑到邻域内拓扑结构的一致性,作者通过引入变换向量之间的距离比值和角度乘积,构成新的距离损失度量函数。最后,通过比较损失值与阈值之间的大小,损失大于阈值的则认为是错误匹配点,否则为正确匹配点。
实现过程
理想刚性变换假设
首先,给定一个候选匹配点集
S
=
{
(
x
i
,
y
i
)
}
i
=
1
N
S=\{(x_i,y_i)\}_{i=1}^N
S={(xi,yi)}i=1N,该点集可以通过SIFT+BF匹配的方式得到。我们的目标是找到一个正确匹配点集
I
∗
I^*
I∗,其能够使得匹配点之间的距离损失函数
C
C
C最小化,即
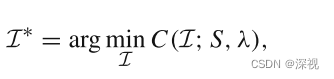
对于理想的刚性变换来说,距离损失函数可以根据匹配点之间的距离差异来计算,如下式
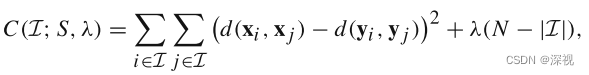
其中,
d
(
,
)
d(,)
d(,)表示距离度量函数,例如欧氏距离;
∣
⋅
∣
|\cdot|
∣⋅∣表示集合的元素的数量,
λ
\lambda
λ表示权重系数。第一项表示原图中的两个点之间的距离,应该与目标图像中对应匹配点之间的距离相近,这对于刚体变换来说是成立的,一个物体上的两个点之间距离,经过刚体变换之后距离保持不变。第二项则是用于惩罚错误匹配点数量的正则项。
广义匹配
上述假设,对于刚性变换是成立的,对于更加复杂的非刚性变换则很难保持了。但在一个较小的邻域范围内,受到物理结构的约束,变换前后两个匹配点邻域范围内其他点的分布情况应该是保持不变的。简单来说就是在原图中
j
j
j是
i
i
i邻域内的点,那么在对应的目标图中
j
j
j也应该是
i
i
i邻域内的点,则距离损失函数改写为
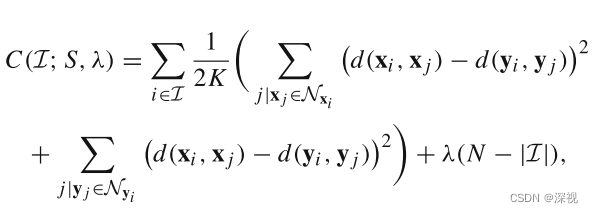
N
x
i
\mathcal{N}_{x_i}
Nxi表示
x
i
x_i
xi的邻域,通过KNN算法得到;
K
K
K表示最近邻的数量。由于非刚性变换中,尺度变化的影响,欧氏距离等距离度量方式不再适用于描述点和点之间的关系,因此距离度量函数采用下式的定义方法
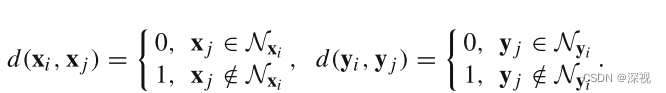
作者还引入了一个新的变量
p
i
∈
{
0
,
1
}
p_i\in \{0, 1\}
pi∈{0,1},用于表示匹配对
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi)是否为正确匹配对,如果是则
p
i
=
1
p_i=1
pi=1,否则
p
i
=
0
p_i=0
pi=0。将新的距离度量函数和
p
i
p_i
pi带入到原距离损失函数中可得
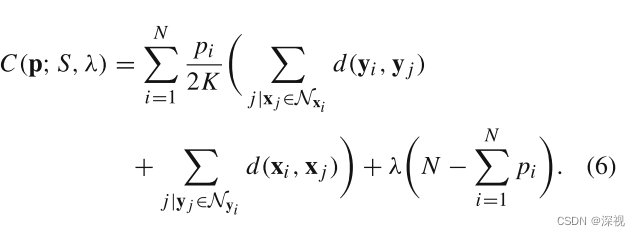
其中对于
x
j
∈
N
x
i
x_j\in \mathcal{N}_{x_i}
xj∈Nxi,其距离
d
(
x
i
,
x
j
)
=
0
d(x_i, x_j)=0
d(xi,xj)=0,同理对于
y
j
∈
N
y
i
y_j\in \mathcal{N}_{y_i}
yj∈Nyi,其距离
d
(
y
i
,
y
j
)
=
0
d(y_i, y_j)=0
d(yi,yj)=0因此原式中的两项被直接约去了。并且由于距离值
d
d
d是个二元量,无非是0或1,因此平方项也没有意义,被省略了。然后我们以
∑
j
∣
x
j
∈
N
x
i
d
(
y
i
,
y
j
)
\sum_{j|x_j\in \mathcal{N}_{x_i}}d(y_i,y_j)
∑j∣xj∈Nxid(yi,yj)这一项为例,看一下他的计算过程
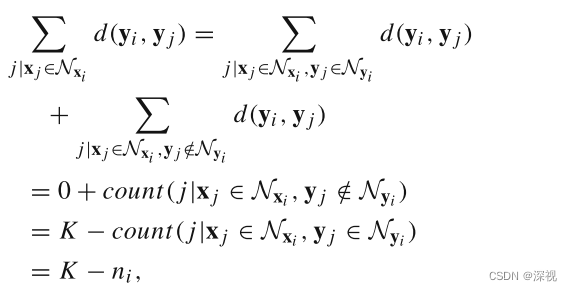
其中
n
i
n_i
ni表示
x
j
x_j
xj属于
x
i
x_i
xi邻域范围内,且
y
j
y_j
yj也属于
y
i
y_i
yi邻域范围内点的数量。同理可知
∑
j
∣
y
j
∈
N
y
i
d
(
x
i
,
x
j
)
\sum_{j|y_j\in \mathcal{N}_{y_i}}d(x_i,x_j)
∑j∣yj∈Nyid(xi,xj)也为
K
−
n
i
K-n_i
K−ni。进而距离损失函数可以写为
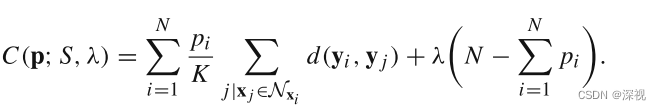
邻域拓扑一致性
上述的距离损失计算过程,只考虑了匹配点邻域范围内其他特征点的分布情况,而没有考虑局部拓扑结构的约束。简单来说,如果在原图中特征点
x
j
x_j
xj在
x
i
x_i
xi的左侧,那么在变换之后的目标图像中
y
j
y_j
yj也应该在
y
i
y_i
yi的左侧,当然这个说法其实是不严谨的,为方便大家理解局部拓扑结构约束的一个意思。那么如何准确的描述这种局部拓扑一致性约束呢,作者引入了两幅图像匹配点之间的位移向量
v
i
v_i
vi。如下图所示,
v
i
v_i
vi是一个由
x
i
x_i
xi指向
y
j
y_j
yj的向量,对于正确匹配的点,其邻域内任意两点之间的位移向量都应该非常接近,而对于错误匹配的点,其邻域内点和点之间的位移向量可能各不相同。
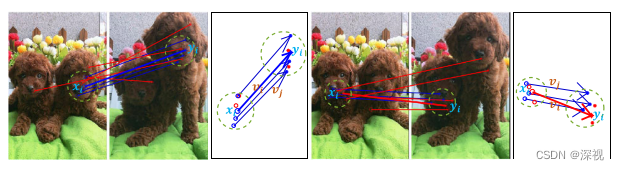
基于上述假设,作者利用两个位移向量之间的长度比值和角度的乘积来描述两个向量之间的一致性
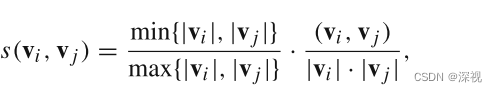
∣
∣
||
∣∣表示L1范数,
(
⋅
,
⋅
)
(\cdot, \cdot)
(⋅,⋅)表示内积计算。那么两个向量之间的距离定义如下
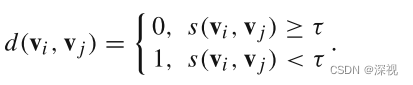
两个向量的相似程度大于等于阈值
τ
\tau
τ则认为距离为0,否则距离为1。引入新的约束条件后,距离损失函数为
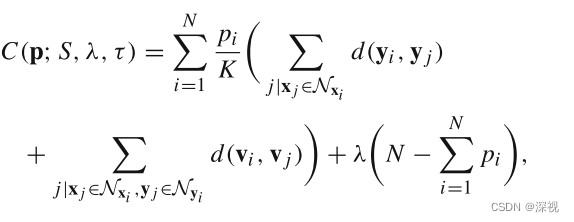
多尺度邻域
考虑到对于不同的图像,特征点的分布情况以及误匹配点所占的比例都是不同的,如果采用固定大小的邻域范围是不合适的。因此作者采用多个
K
K
K的取值,
K
=
{
K
m
}
m
=
1
M
\mathbf{K}=\{K_m\}_{m=1}^M
K={Km}m=1M,分别进行计算距离损失,然后在计算平均值作为最终的距离损失
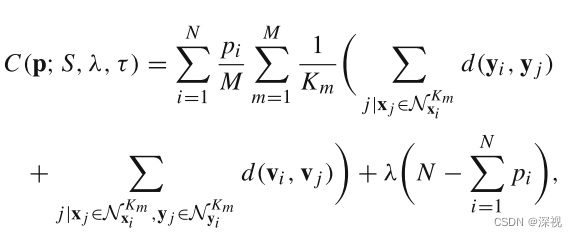
求解
上述损失函数经过合并项后,可以简化为
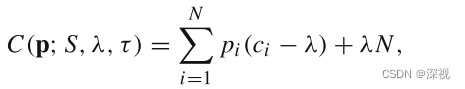
其中
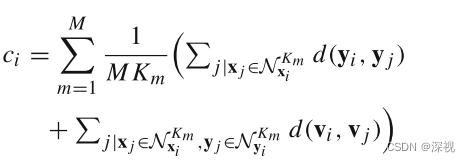
我们的优化目标是寻找最优的
p
=
{
p
i
}
\mathbf{p}=\{p_i\}
p={pi}使得损失函数
C
C
C最小。一个直接的求解思路就是,如果
c
i
>
λ
c_i>\lambda
ci>λ,我们就令
p
i
p_i
pi为0,否则令
p
i
=
1
p_i=1
pi=1,这样就能使的损失函数
C
C
C最小,即
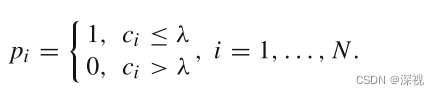
最终的匹配点集为
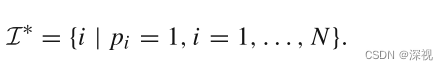
邻域构建
原本邻域是在整个候选匹配点集
S
S
S中选择最近邻点构建的,则邻域中既有正确匹配点也有错误匹配点。如果能够只在正确匹配点集中选择最近邻点构建邻域,保证邻域内的点都是正确匹配点,这样能过够让正确匹配点之间的相似性更高,而错误匹配点的邻域内的拓扑一致性无法保持,因此距离更大。如何能够尽可能地在正确匹配点集中构建邻域呢?这可是我们地求解目标呀。作者想到了迭代地方式,第一次匹配可以得到一个近似的正确匹配点集
I
0
I_0
I0。在这个基础上重新构建邻域,再次匹配得到最终的匹配点集
I
∗
I^*
I∗
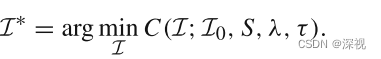
算法的伪代码如下

创新点
- 提出邻域拓扑一致性的距离计算方法,用于度量两个匹配点之间的距离
- 提出多尺度和迭代的邻域构建方法
算法评价
本文可以看作是LGSC的出处,LGSC算法基本延续了LPM的算法思想,只是在距离度量函数上略有不同。作者认为这类方法也属于图匹配的类别,但规避了图匹配所带来的计算负担,使其能够在线性时间内求解。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。