1 基本测速原理——多普勒频移

1.0 写在前面

振动/波在空间中传播有三个关键变量，分别是波长、波速、频率。三者的数学关系如下
$V=\lambda f$
毫米波本质上是一种电磁波，因此其波速等于光速，为3x10的8次方。速度一定的情况下，一定时间内波在空间中传播的距离是一定的。一个周期T内传播的距离就是一个波长，所以，波长本质上表示距离。

1.1 多普勒效应

多普勒效应（Doppler effect）是波源与观察者有相对运动时，观察者接受到波的频率与波源发出的频率并不相同的现象。生活中比较常见的例子是远方急驶过来的火车鸣笛声变得尖细（即频率变高，波长变短），而离我们而去的火车鸣笛声变得低沉（即频率变低，波长变长）。

1.2 多普勒频移

1.1节所述为多普勒效应的内容，可以知道多普勒效应的本质是波源与观察者之间波的频率的差别，本节详细解释相对运动与频率的数学关系。

初始关系如下图所示，
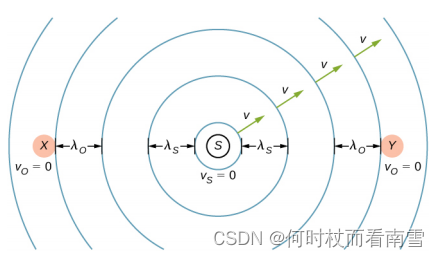
$\begin{array}{c} 波源S保持静止，V_{s} = 0，均匀向四周辐射波长为\lambda _{s},波速为V的波\\ 有两个接收源X和Y，均保持静止，他们接收到波源S辐射的波长为\lambda _{o}\\ 由于此时源和接收者之间没有相对运动，因此\lambda _{s} = \lambda _{o} \end{array}$
在这里插入图片描述
$\begin{array}{c} 从某一时刻开始，波源S以V_{s}的速度向Y运动，运动时间为一个周期T _{s}，其他参数不变\\ 四幅图分别表示T = 0，T=T _{s}，T=2T _{s}，T=3T _{s}，\\ 图中实线表示对应时刻波辐射的位置。虚线表示对应时刻之前波辐射的位置 \end{array}$
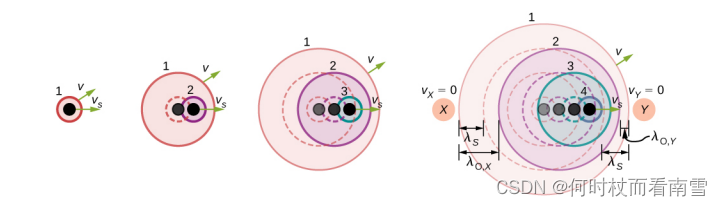
在这里插入图片描述
根据图片内容，很容易得出，相对于X
$\begin{aligned} \lambda_{o} &=\lambda_{s}+\Delta x \\ v T_{o} &=v T_{s}+v_{s} T_{s} \\ \frac{v}{f_{o}} &=\frac{v}{f_{s}}+\frac{v_{s}}{f_{s}}=\frac{v+v_{s}}{f_{s}} \\ f_{o} &=f_{s}\left(\frac{v}{v+v_{s}}\right) \end{aligned}$
相对于Y，有
$\begin{aligned} \lambda_{o} &=\lambda_{s}-\Delta x \\ v T_{o} &=v T_{s}-v_{s} T_{s} \\ \frac{v}{f_{o}} &=\frac{v}{f_{s}}-\frac{v_{s}}{f_{s}}=\frac{v-v_{s}}{f_{s}} \\ f_{o} &=f_{s}\left(\frac{v}{v-v_{s}}\right) . \end{aligned}$

疑问

从上面的分析和众多的资料中都显示，多普勒频移是直接影响到一个连续波的频率，波的相位仍然保持连续，如下图所示。请添加图片描述

请添加图片描述
不知道有没有人跟我一样对Doppler shift 频率改变相位连续表示过怀疑，这些怀疑基于：

波在离开波源后，理想情况下是没有任何外作用力可以改变波的任何参数，就像断了线的风筝一样不受控制，自由在空间中极化与传播，因此Doppler频移一定不是在传播过程中被改变的。
正常情况下，一个未被频率调制的波在空间中的传播可以理解为一个sin函数，如果是在真空中传播且没有遮挡，那么理论上这个sin函数是可以传播无限远的。
波源移动导致相邻波之间有一个Vs*T的波程差，最终的波不应该是相位上有差别而频率不会被改变吗？

解答：
波源是在移动过程中产生波，以上的讨论波是连续生成的，所以在波源移动过程中，波相当于被调制了，因此产生那样的Doppler shift。

2 LFMCW雷达测速原理

2.1 Doppler Shift 到底是调频还是调相

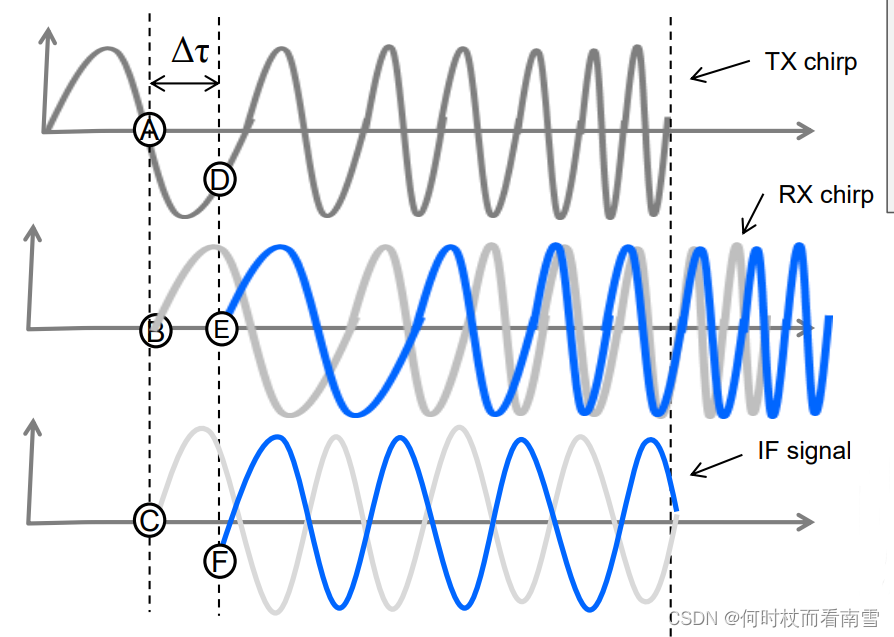
个人拙见，Doppler Shift本质上是调相，由于上面1节是关于波源发射连续波并以恒定速度进行运动的理想场景，对波调相刚好可以等效为调频，因此叫Doppler 频移，但是LFMCW调频波的发送是间隔的非连续的，因此虽然LFMCW雷达的也叫Dopple shift，但其本质上已经是在分析相位的变化了。
这一点，我们可以从德州仪器关于TI毫米波雷达测速方面的讲解视频得知。所以需要分析相位随时间变化的关系。
在这里插入图片描述

2.2 为什么是二维FFT

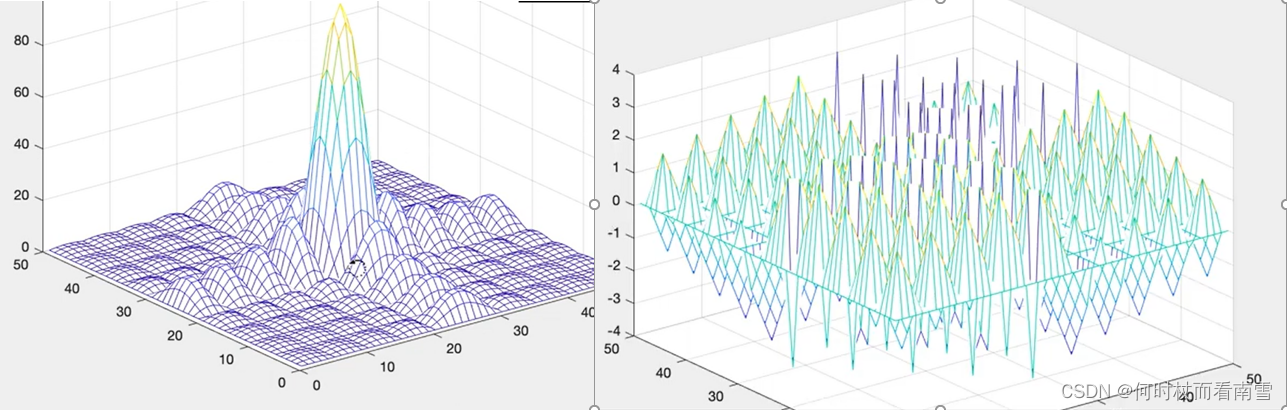
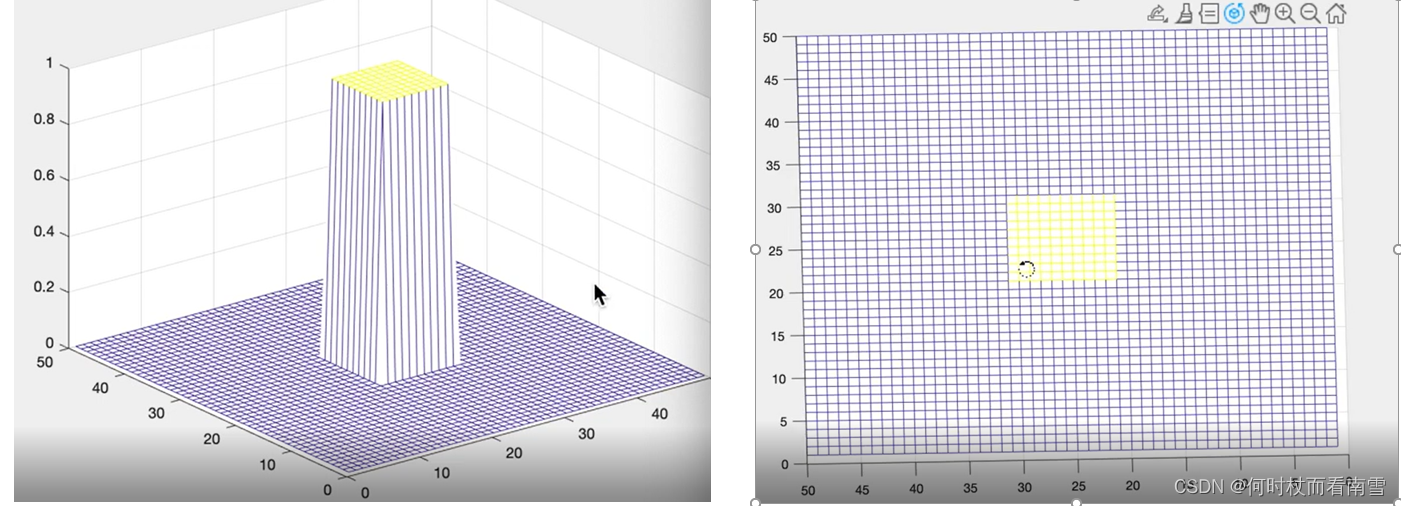
对于矩阵数据的二维FFT处理更多的其实是在Image Processing这个领域当中，图像处理领域认为2DFFT和信号的相位有着天然的联系，当然这种认知背后是有严谨的数学推理和论证过程的，这里就不进行公式的推导了，给大家上几幅图直观的感受一下，2DFFT和信号相位的关系。如下图所示的信号，在矩阵中心n*n窗口内值为1，其三维图和俯视图如下所示。
在这里插入图片描述
下图为上述图像分别做2DFFT的幅频图像和相频图像

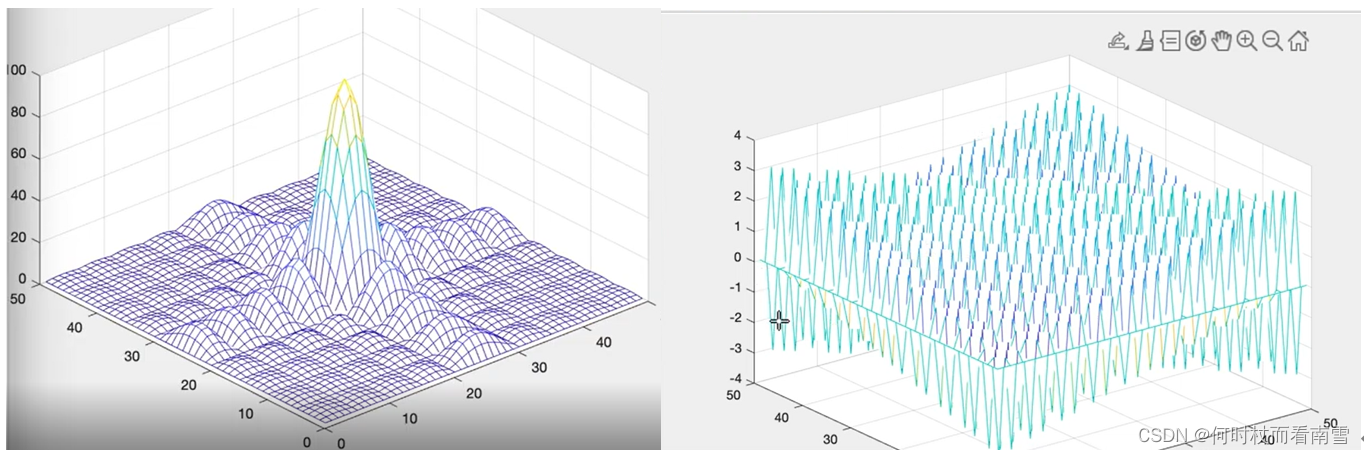
请大家记住上面的幅频图像和相频图像，然后我们原始图像什么都不做，仅仅改变原始图像的相位，幅度为1的矩阵由中心移动到边缘，改变后的图像时域如下图所示
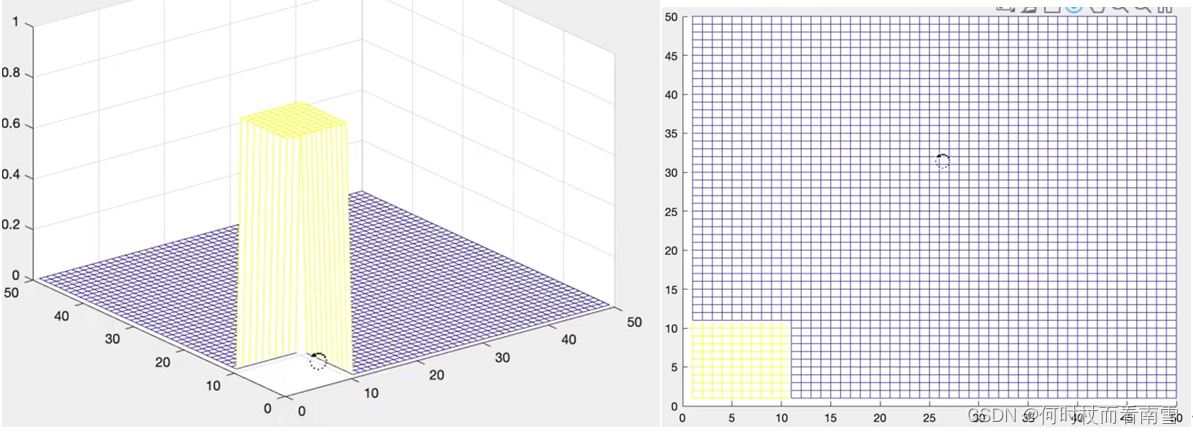
在这里插入图片描述
我们来看上述图像的2DFTT的结果，观察其幅频曲线和相频曲线，然后奇妙的事情发生了，2DFFT的幅度函数和原来保持一样，相位却发生了改变！！！