文章目录
- 一.二叉树的概念及结构
- 1.1概念
- 1.2特殊的二叉树
- 二.二叉树的性质
- 三.小练习
- 3.1
- 3.2
- 3.3
一.二叉树的概念及结构
不熟悉树这个结构的可以看看数据结构:树这篇文章。
1.1概念
一棵二叉树是结点的一个有限集合,该集合:
- 为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
像这样: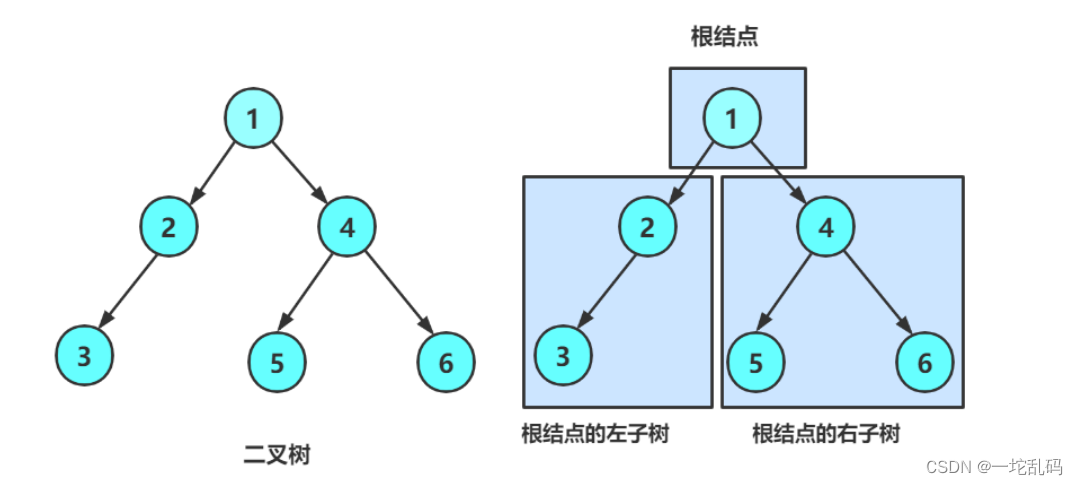
每个节点都有2个或1个或者0个子节点,这就是二叉树。而且
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
任意二叉树都是由以下几种情况构成的:
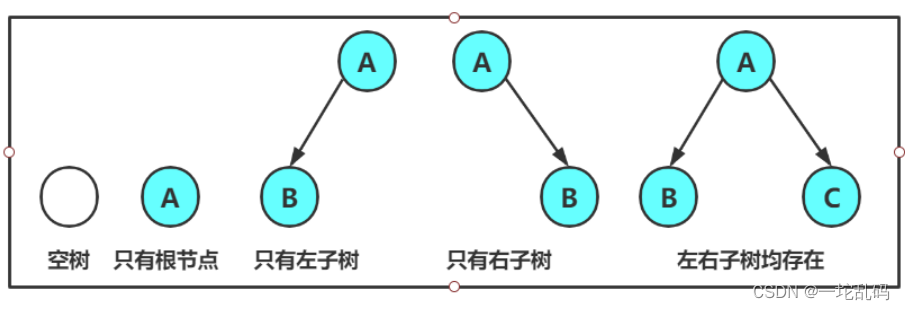
1.2特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。像这样
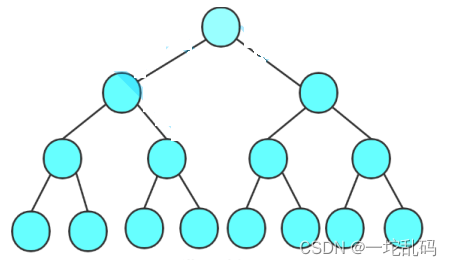
像这样除了最后一行,每一行的节点都有两个节点。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。像这样
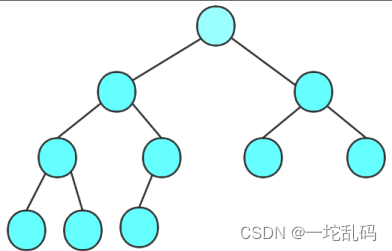
简单来讲完全二叉树就是最后一行的节点最少为1个,最多为2 ^ (n-1)个节点(n为此时的高度)并且从左到右要连续.而节点为2 ^ (n-1)时此时的完全二叉树就是满二叉树。
二.二叉树的性质
我们观察一下完全二叉树:
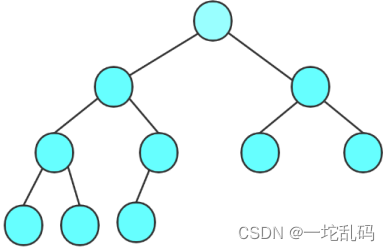
- 来看这棵树的每一层都有多少个节点,通过计算不难算出,如果此时高度是i的话则一棵非空二叉树的第i层上最多有2 ^ (i-1)个结点。
- 那深度为n的二叉树的最大结点数是多少呢?也就是深度为n的满二叉树的节点有多少。我们可以列一个式子:
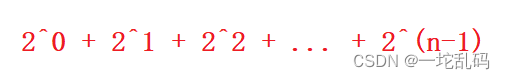
学过高中数学的应该能一眼看出来这是一个等比数列的前n项和结果就是:2^n - 1;但是这是完全二叉树也就是满二叉树最大的节点数,那最小的节点数是多少呢?这也不难算,最少节点个数就相当于最后一行只有1个节点,结果可以认为前(n-1)个节点的个数+1:
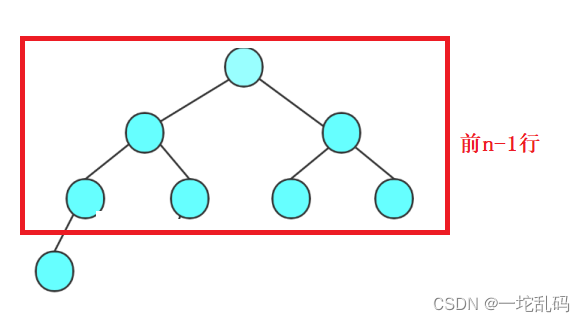
结果就是2 ^ (n-1) -1 + 1,也就是2 ^ (n-1).
-
再来计算一下如果这个数有i个节点,它的深度n是多少?既然刚才计算了总结点数 i = 2 ^ n - 1。那倒过来退n应该等于log(i + 1)这里是以2为底,但是我打出来那个2,所以就这样表示了。

-
最后还有一个比较重要的性质:对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2,则有n0= n2+1.就是没有孩子的节点永远比有两个孩子节点的个数多一个。
当然这个二级结论可以推到出来的:
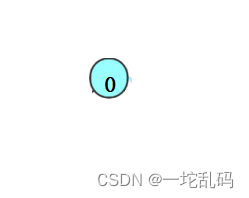
刚开始这里只有一个节点,他没有孩子所以没有孩子的节点为1个n0 = 1,有两个孩子节点的没有n2 = 0.
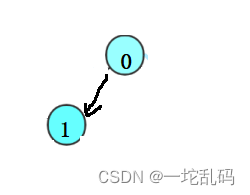
现在多加一个节点没有孩子的节点是1这个节点仍然只有1个n0 = 1,而有两个孩子的节点还是没有n2 = 0;
再添加一个节点发现终于有一个节点有两个孩子了,n2 = 1,但是呢此时没有孩子的节点是1,2这两个节点变成了2个,n0 = 2.仍然比n2多一个,后来的步骤都差不多,所以说n0用于比n2多1.
三.小练习
看几道简单的练习:
3.1

这里就要用到刚才推导出来的结论:
n0 = n2 + 1;
而叶子节点数就是度为0的节点,所以这题答案是199+1
3.2

因为二叉树中节点的度只有三种0,1,2也就是说
n0 + n1 + n2 = 2n,而现在我们求的是n0的个数:
n0 + n1 + n2 = 2n;
n0 + n0 - 1 + n1 = 2n;
2*n0 = 2n + 1 - n1;
而现在我们唯一不知道的就是n1的值,但是注意只有一个度的节点只有两种情况:
要么为1:
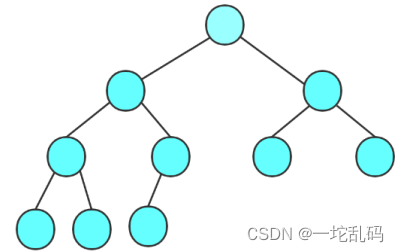
要么为0:
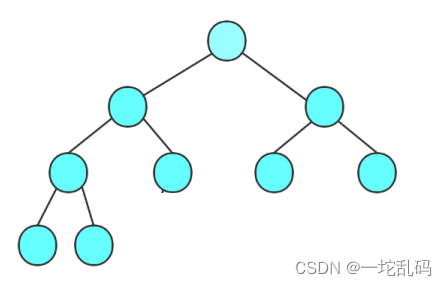
我们再看刚才得出的式子:
2*n0 = 2n + 1 - n1此时n1不可能为0,一旦为0了,那n0的个数就变成了n + 1/2,这显然是不合理的,所以只有一个度的节点个数只能是0,叶子节点个数自然而然就等于n了。
3.3

节点个数和数的高度的关系,之前也算出来了:
最大节点个数 = 2 ^ 高度 - 1.
最小节点个数 = 2 ^ (高度).
通过估算2的9次方是512,碰巧531是在2的9次方和10次方之间。所以这个树的高度是10.