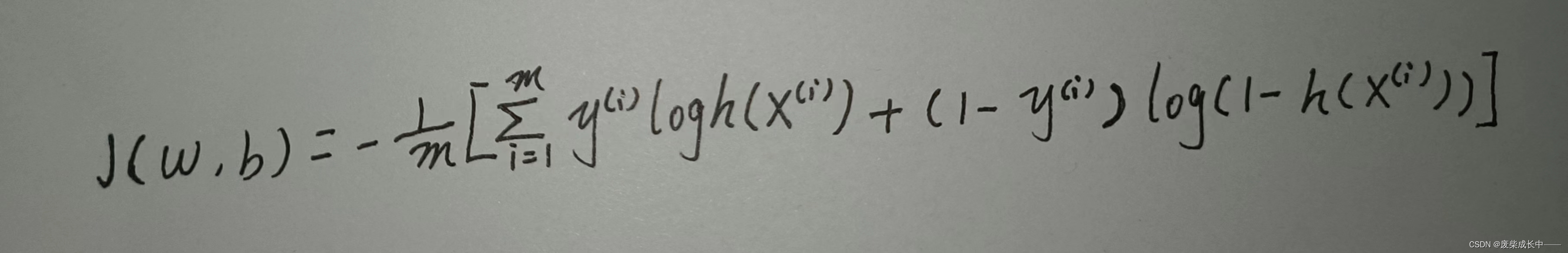损失函数：

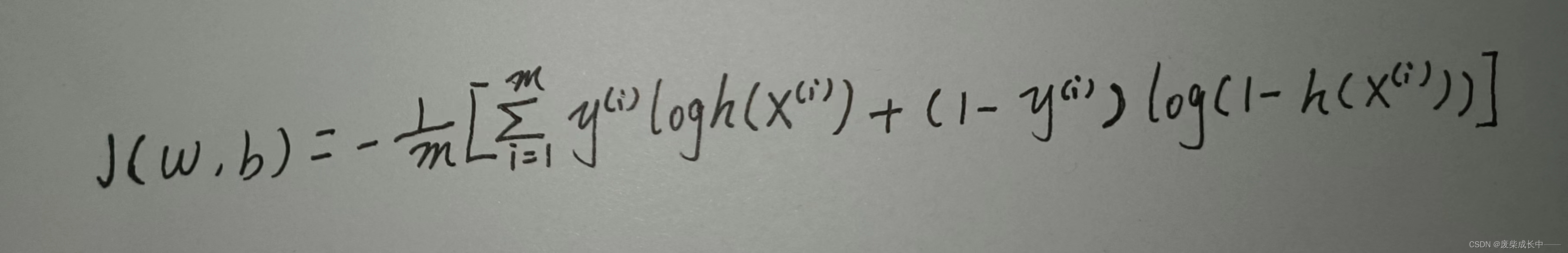
之前一直想不明白这个式子为什么可以当损失函数。所以记录一下。

首先，假如一个属于1类的样本，经过预测，h(x)=0.3,得出0.3的概率是属于1类，也就是0.7的概率是属于0类，那么其误差就是0.7。
相反，一个属于0类的样本，经过预测，h(x)=0.7,得出有0.7的概率是属于1类。那么其误差就是0.7。可以看出两种情况误差相等。

对于1类样本来说，h(x)越大，误差越小，所以要有一个递减函数来套住h(x)，且当h(x)等于1时函数要等于0（预测正确，误差为0）。log函数就再适合不过。
log本身是递增函数，所以到前面加一个负号将其变为递减。其次log1等于0。

-logh(x)就是预测1类样本的误差。

对于0类样本来说，h(x)越大，误差越大。h(x)越小，误差越小。h(x)等于0时，误差为0。1-h(x)表示样本为0的概率。还是放入log函数，变为-log(1-h(x))。

到这里好像挺简单的。但是！在计算的时候，还来个if else来分个1类还是0类来分别计算它们的误差吗？

不不不，前人早就想好了，只需要对式子稍作修改。使损失函数在y=0时计算1类的式子-logh(x)不存在。在y=1时计算0类的式子-log(1-h(x))不存在。反正y不是1就是0。那就拿y亲自上阵呗。
y=0时就拿y乘以求1类样本损失的式子。y=1时就拿(1-y)乘以求0类样本损失的式子,不可以是乘以（y-1）。因为(y-1)当y=0时，式子变成(y-1)[-log(1-h(x))]= -[-log(1-h(x))]=log(1-h(x)),算的误差就成负数了。这里同统一误差算正数。

所以就得到了以下式子：
-ylogh(x)+(1-y)[-log(1-h(x))]
也就是计算其中一个样本的误差式子。

那么计算m个样本的平均误差就是：