Problem - 1445D - Codeforces

题意:

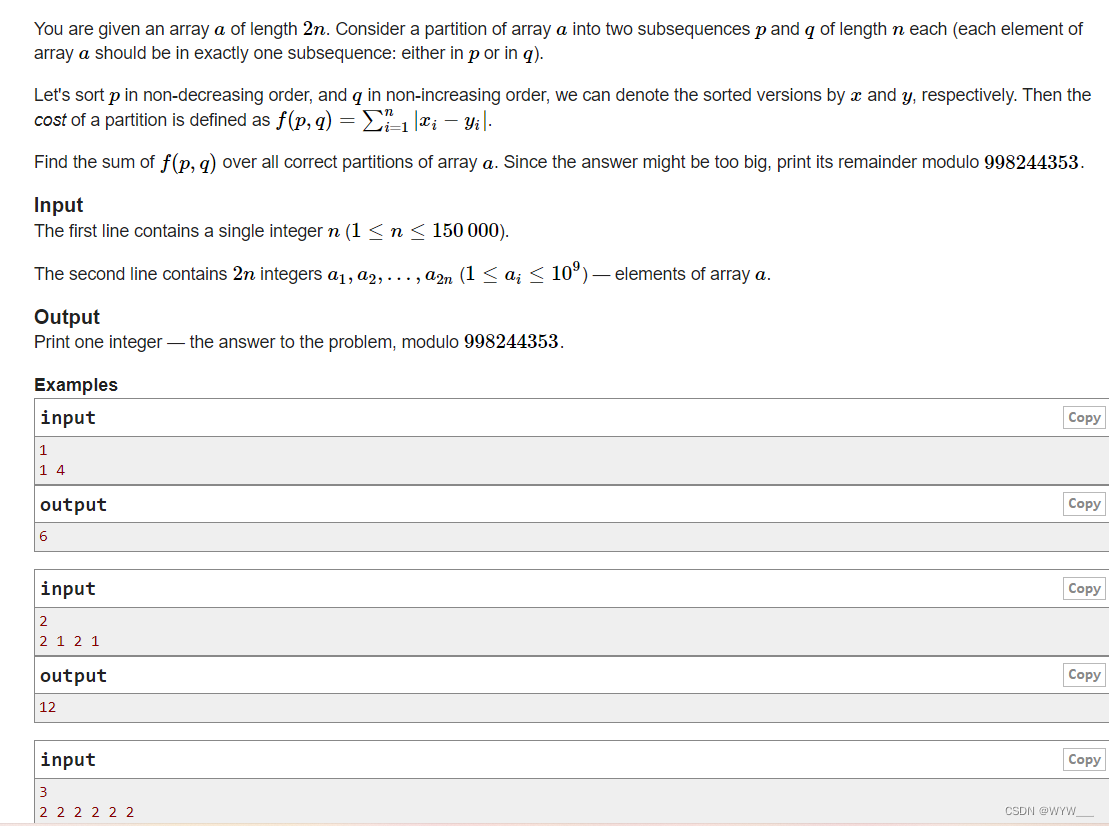
给你一个长度为2n的数组a。考虑将数组a划分为两个子序列p和q，每个子序列的长度为n（数组a的每个元素应该正好在一个子序列中：要么在p中，要么在q中）。

让我们以非递减顺序对p进行排序，以非递增顺序对q进行排序，我们可以分别用x和y来表示排序后的版本。那么一个分区的成本被定义为f(p,q)=∑ni=1|xi-yi|。

求数组a所有正确分区的f(p,q)之和。由于答案可能太大，请打印其余数，即998244353。

输入
第一行包含一个整数n（1≤n≤150000）。

第二行包含2n个整数a1,a2,...,a2n（1≤ai≤109）--数组a的元素。

输出
打印一个整数 - 问题的答案，模数998244353。

例子
输入复制
1
1 4
outputCopy
6
输入副本
2
2 1 2 1
输出拷贝
12
输入复制
3
2 2 2 2 2 2
输出拷贝
0
输入复制
5
13 8 35 94 9284 34 54 69 123 846
输出拷贝
2588544
注意
如果一个数组的两个分区包含在子序列p中的元素索引集不同，则认为是不同的。

在第一个例子中，有两个正确的数组a的分区。

p=[1], q=[4], 那么x=[1], y=[4], f（p,q）=|1-4|=3;
p=[4], q=[1], then x=[4], y=[1], f(p,q)=|4-1|=3.
在第二个例子中，数组a有六个有效分区。

p=[2,1], q=[2,1]（原数组中指数为1和2的元素在子序列p中被选中）。
p=[2,2], q=[1,1];
p=[2,1], q=[1,2]（在子序列p中选择指数为1和4的元素）。
p=[1,2], q=[2,1];
p=[1,1], q=[2,2];
p=[2,1], q=[2,1]（指数为3和4的元素在子序列p中被选中）。

题解:
题意很简单,本题关键处在于能否看出构建出的序列得到的之都相等

我们列几个例子就可以发现

//1 2 3 4 5 6
//3 2 1
//4 5 6    9

//6 2 1
//3 4 5    9

只要是符合的结果肯定都一样

先排序一下计算,得出一个的成本

剩下的就是看有多少种情况即可,从2*n里去n个,答案很明显,组合数

#include<iostream>
#include<algorithm>
#include<map>
#include<queue>
#include<vector>
#include<cstring>
#include<stack>
using namespace std;
long long n;
long long a[400000];
long long fac[400000];
long long infac[400000]; 
int mod = 998244353;
long long qpow(long long a,long long x)
{
	long long ans = 1;
	while(x)
	{
		if(x&1)
		ans = ans*a%mod;
		a = a*a%mod;
		x = x/2;
	}
	return ans;
}
void solve()
{
	int n;
	cin >> n;
	for(int i = 1;i <= n*2;i++)
	cin >> a[i];
	sort(a+1,a+1+2*n);
	long long ans = 0;
	for(int i = 1;i <= n;i++)
	{
		ans = (ans+a[i+n]-a[i]+mod)%mod;
	}
	infac[1] = 1;
	fac[1] = 1;
	for(int i = 2;i <= 2*n;i++)
	{
		fac[i] = (fac[i-1]*i)%mod;
		infac[i] = infac[i-1]*qpow(i,mod-2)%mod;
	}
	cout<<ans*fac[2*n]%mod*infac[n]%mod*infac[n]%mod;
}
int main()
{
	int t = 1;
//	cin >> t;
	while(t--)
	{
		solve();
	}
}
//1 2 3 4 5 6
//3 2 1
//4 5 6    9

//6 2 1
//3 4 5    

//c 5 2
//a5 /  a2 a3