目录
2.1 什么是命题
2.1.1 命题的定义
2.1.2 复合命题
2.2 命题联结词
2.2.1 否定联结词
2.2.2 合取联结词
2.2.3 析取联结词
2.2.4 蕴涵联结词
2.2.5 等价联结词
2.3 命题符号化及应用
2.3.1 命题连接词总结
2.3.2 命题联结词的优先级
2.3.3 命题联接词与开关电路
2.3.4 命题联接词与逻辑电路
2.3.5 命题联接词与网页检索
2.3.6 命题联接词与位运算
2.4 命题公式和真值表
2.4.1 命题变元
2.4.2 命题公式
2.4.3 公式的解释
2.4.4 真值表
2.5 公式的分类和逻辑等价
2.5.1 命题公式分类
2.5.2 公式的等价
2.5.3 公式等价的充分必要条件
2.5.4 命题公式的可判定性
2.6 基本等价关系及其应用
2.6.1 基本等价关系
2.6.2 判断公式类型
2.6.3 证明公式等价
2.6.4 开关电路化简
2.6.5 逻辑电路化简
2.6.6 解决推理问题
2.1 什么是命题
2.1.1 命题的定义
具有确切真值的陈述句称为命题(proposition)。该命题可以取一个“值”,称为真值。真值只有“真”和“假”两种,分别用“T”(或“1”) 和“F”(或“0”)表示。
数理逻辑研究的中心问题是推理,而推理的前提和结论都是命题。因而命题是推理的基本单位。
一切没有判断内容的句子,如命令句 (或祈使句)、感叹句、疑问句、二义性的陈述句等都不能作为命题。
2.1.2 复合命题
原子命题 (简单命题):不能再分解为更为简单命题的命题。
复合命题:可以分解为更为简单命题的命题。这些简单命题之间是通过如“或者”、“并且”、“不”、“如果......则......”、“当且仅当”等这样的关联词和标点符号复合而成。
约定:通常用大写的带或不带下标的英文字母表示命题 (包括原子命题和复合命题)
A,B,C,· · · ,P,Q,R,· · · , Ai,Bi,Ci,· · · ,Pi,Qi,Ri,· · ·
2.2 命题联结词
2.2.1 否定联结词
设 P 是任意一个命题,复合命题“非 P”(或 “P 的否定”)称为 P 的否定式(negation),记作¬P,“¬” 为否定联结词。P 为真当且仅当 ¬P 为假。“¬” 是自然语言中的 “非”、“不”、“没有” 等的逻辑抽象。
例如
P:四川是一个国家
¬P:四川不是一个国家
| P | ¬P |
| 0 | 1 |
| 1 | 0 |
2.2.2 合取联结词
设 P、Q 是任意两个命题,复合命题“P 并且 Q”(或 “P 和 Q”)称为 P 与 Q 的合取式(conjunction),记作P ∧ Q,“∧” 为合取联结词。P ∧ Q 为真当且仅当 P,Q 同为真。
例如
P:3 是素数;
Q:3 是奇数。
P ∧ Q:3 既是素数又是奇数
| P | Q | P ∧ Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
“∧” 是自然语言中的 “并且”、“既…又…”、“但”、“和”、“与”、“不仅…而且…”、“虽然…但是…”、“一面…, 一面…” 等的逻辑抽象;但不是所有的“和”,“与”都要使用合取联结词表示,要根据句子的语义进行分析。
例如以下这两个命题都是简单命题,不能再分。
- 2和3的最小公倍数是 6
- 点a位于点b与点c之间
2.2.3 析取联结词
设 P、Q 是任意两个命题,复合命题“P 或 Q”称为 P 与 Q 的析取式(disjunction),记作P ∨ Q,“∨” 为析取联结词。P ∨ Q 为真当且仅当 P,Q 至少有一个为真。
例如
P:张谦是大学生
Q:张谦是运动员
P ∨ Q:张谦是大学生或是运动员
| P | Q | P ∨ Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
联结词 “∨” 是自然语言中的 “或”、“或者” 等的逻辑抽象。自然语言中的 “或” 有 “可兼或”(或称为同或)、“不可兼或”(即异或) 两种。严格来讲,析取联结词实际上代表的是可兼或,异或有时会使用单独的异或联结词 “⊕” 来表示。
例如
命题:张红生于 1982 年或 1983 年,令
- P: 张红生于 1982 年;
- Q: 张红生于 1983 年。
P 与 Q 不能同时为真,即为“不可兼或”
2.2.4 蕴涵联结词
设 P、Q 是任两个命题,复合命题“如果 P,则 Q”称为 P 与 Q 的蕴涵式(implication),记作P → Q,“→” 为蕴涵联结词。P → Q 为假当且仅当 P 为真且 Q 为假。一般把蕴涵式 P → Q中的 P 称为该蕴涵式的前件,Q 称为蕴涵式的后件。
例如
- P:周末天气晴朗
- Q:我们将到郊外旅游
- P → Q:如果周末天气晴朗,则我们将到郊外旅游
| P | Q | P → Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
在自然语言中,前件为假,不管结论真假,整个语句的意义,往往无法判断。但对于数理逻辑中的蕴涵联结词来说,当前件 P 为假时,不管 Q 的真假如何,则 P → Q 都为真。此时称为 “善意推定”。
例如
命题:如果角 A 和角 B 是对顶角,则角 A 等于角 B。
这个命题是我们非常熟悉的一个定理,当然是真命题。当前件为假时,这个定理依然成立。
设 P:约翰学习微积分,Q:约翰是大学一年级学生。则以下的复合命题均可用 P → Q 表示。
- 如果约翰学习微积分,则他是大学一年级学生。如果 P,则 Q
- 因为约翰学习微积分,所以他是大学一年级学生。因为 P,所以 Q
- 只要约翰学习微积分,他就是大学一年级学生。只要 P,就 Q
- 约翰学习微积分仅当他是大学一年级学生。P 仅当 Q
- 只有约翰是大学一年级学生,他才能学习微积分。只有 Q,才 P
- 除非约翰是大学一年级学生,他才能学习微积分。除非 Q,才 P
- 除非约翰是大学一年级学生,否则他不学习微积分。除非 Q,否则 ¬P
2.2.5 等价联结词
设 P、Q 是任两个命题,复合命题“P 当且仅当 Q”称为 P 与 Q 的等价式(equivalence),记作P ↔ Q,“↔” 为等价联结词(也称作双条件联结词)。P ↔ Q 为真当且仅当 P、Q 同为真假。“↔” 是自然语言中的 “等价”、“充分必要条件”、“当且仅当” 等的逻辑抽象。
例如
- P:两个三角形全等;
- Q:三角形的三条边全部相等
- P ↔ Q:两个三角形全等当且仅当三角形的三条边全部相等
| P | Q | P ↔ Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2.3 命题符号化及应用
2.3.1 命题连接词总结
| 联结词 | 记号 | 复合命题 | 读法 | 记法 | 真值结果 |
| 否定 | ¬ | P的否定 | 非 P | ¬P | ¬P 的真值为“真” 当且仅当 P 的真值为“假” |
| 合取 | ∧ | P 并且 Q | P 合取 Q | P∧Q | P ∧ Q 的真值为“真” 当且仅当 P、Q 的真值同为“真” |
| 析取 | ∨ | P 或者 Q | P 析取 Q | P∨Q | P ∨ Q 的真值为“真” 当且仅当 P、Q 的真值至少一个为“真” |
| 蕴涵 | → | 若 P,则 Q | P 蕴涵 Q | P→Q | P→Q 的真值为“假”当且仅当P 的真值为“真”、Q的真值为“假” |
| 等价 | ↔ | P 当且仅当 Q | P等价于Q | P ↔Q | P ↔Q 的真值为“真”当且仅当P、 Q的真值同为“真”或同为“假” |
命题联接词 “∧”、“∨”、“↔” 具有对称性,而 “¬”、“→” 没有
| P | Q | ¬P | P∧Q | P∨Q | P→Q | P ↔Q |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
联结词是两个命题真值之间的联结,而不是命题内容之间的连接,因此复合命题的真值只取决于构成他们的各简单命题的真值,而与它们的内容无关,与二者之间是否有关系无关。
2.3.2 命题联结词的优先级
优先级顺序
- 所有五个联接词的优先顺序为:否定,合取,析取,蕴涵,等价;
- 同级的联结词,按其出现的先后次序 (从左到右);
若运算要求与优先次序不一致时,可使用括号;同级符号相邻时,也可使用括号。括号中的运算为最高优先级。
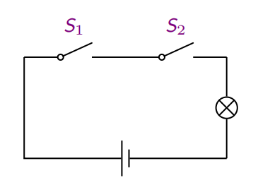
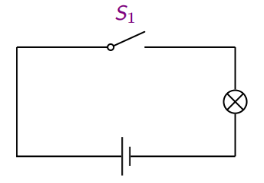
2.3.3 命题联接词与开关电路
设命题 P;开关 S1 闭合;命题 Q;开关 S2 闭合。
开关电路的 “串联”:P ∧ Q
开关电路的 “并联”:P ∨ Q
开关电路的 “断开”:¬P
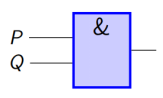
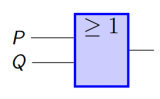
2.3.4 命题联接词与逻辑电路
命题联接词 “∧”、“∨”、“¬” 对应于与门、或门和非门电路,从而命题逻辑是计算机硬件电路的表示、分析和设计的重要工具。
与门:P ∧ Q
或门:P ∨ Q
非门:¬P
2.3.5 命题联接词与网页检索
布尔检索
在布尔检索中,联接词 “∧”(一般用 AND 表示)用于匹配包含两个检索项的记录,联接词 “∨”(一般用 OR 表示)用于匹配包含两个检索项至少一个的记录,而联接词 “¬”(一般用 NOT 表示)用于排除某个特定的检索项.
2.3.6 命题联接词与位运算
位运算
计算机中的信息采用二进制的方式来表达。每个二进制位只能是 1 或 0,可对应于某一个布尔变量的真值。当我们需要判断该布尔变量的真值时,就可以利用按位与(bitwise AND)或按位或(bitwise OR)以及按位取反(bitwise NOT)等来操作。
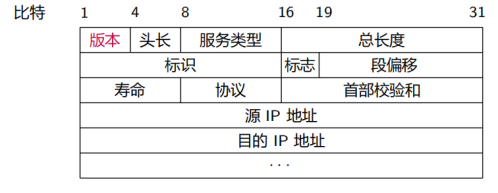
这是 TCP/IP 网络协议栈中的 IP 报头的基本格式,考虑:如何获取版本号?
答案:ipdata[0]&0xF0 >> 4
2.4 命题公式和真值表
2.4.1 命题变元
一个特定的命题是一个常值命题,它不是具有值 “T”(“1”),就是具有值 “F”(“0”)。
一个任意的没有赋予具体内容的原子命题是一个变量命题,常称它为命题变量(或命题变元)(propositional variable),该命题变量无具体的真值,它的变域是集合{T, F}(或 {0, 1})。
复合命题是由原子命题与联结词构成的命题。所以,当其中的原子命题是命题变元时,此复合命题也即为命题变元的函数,且该函数的值仍为“真”或“假”值,这样的函数可形象地称为“真值函数” 或 “命题公式”,此命题公式没有确切的真值。
2.4.2 命题公式
命题演算的合式公式 (well formed formula,wff),又称命题公式 (简称公式),按如下规则生成:
- 命题变元本身是一个公式;(如:P, Q, R, · · · )
- 如 G 是公式,则(¬G)也是公式;(如:¬P, ¬Q, ¬R, · · · )
- 如 G,H 是公式,则(G ∧ H)、(G ∨ H)、(G → H)、(G ↔ H)也是公式;(如:P ∧ Q,(¬Q) → R, · · · )
- 仅由有限步使用规则 (1)、(2)、(3)后所得到的包含命题变元、联结词和括号的符号串才是命题公式.(如:¬(P ∧ Q) ↔ R,(¬Q ∨ (P ∧ ¬R)) → R, · · · )
如果 G 是含有 n 个命题变元 P1、P2、P3、· · · 、Pn 的公式,可记为:G(P1, P2, P3, · · · , Pn) 或简写为 G。
关于命题公式的说明
- 原子命题变元是最简单的合式公式,称为原子合式公式,简称原子公式
- 命题公式没有真值,只有对其命题变元进行真值指派后,方可确定命题公式的真值
- 整个公式的最外层括号可以省略;公式中不影响运算次序的括号也可以省略
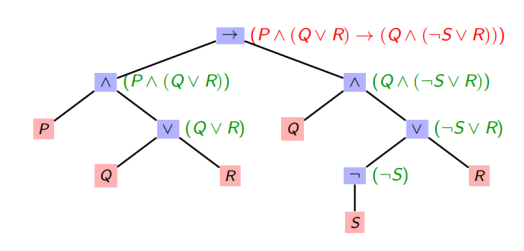
- 在实际应用中,为了便于存储和运算,命题公式常用二元树的方式来表达
2.4.3 公式的解释
定义
设 P1、P2、P3、· · · 、Pn 是出现在公式 G 中的所有命题变元,指定 P1、P2、P3、· · · 、Pn 一组真值,则这组真值称为 G 的一个解释,常记为 I。
如果公式 G 在解释 I 下是真的,则称I 满足 G,此时 I 是 G 的成真赋值;如果 G 在解释 I 下是假的,则称I 弄假于 G,此时 I 是 G 的成假赋值。
2.4.4 真值表
一般来说,若有 n 个命题变元,则应有 2^n 个不同的解释。
利用真值表,可得到公式的所有成真赋值和成假赋值。
定义
由公式 G 在其所有可能的解释下所取真值构成的表,称为 G 的真值表(truth table)。一般我们将公式中的命题变元放在真值表的左边,将公式的结果放在真值表的右边。有时为了清楚起见,可将求公式的中间结果也放在真值表中。
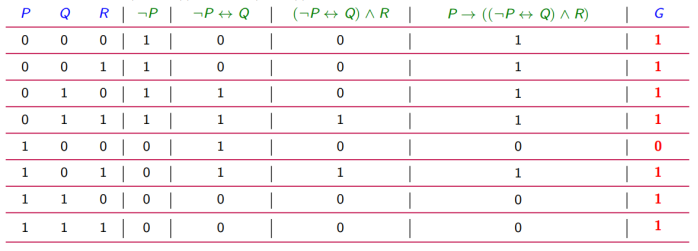
例如公式G=P→((¬P ↔Q)∧R)
2.5 公式的分类和逻辑等价
2.5.1 命题公式分类
我们先来看下面一组公式的真值表
- G1 = ¬(P → Q) → P
- G2 = (P → Q) ∧ P
- G3 = ¬(P ∧ ¬Q) ↔ ¬(P → Q)
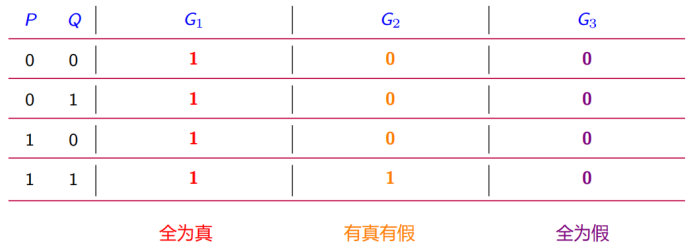
定义
- 公式G称为永真公式(重言式,tautology),如果在它的所有解释之下其真值都为“真”。
- 公式G称为永假公式(矛盾式,contradiction),如果在它的所有解释之下其真值都为“假”。有时也称不可满足公式。
- 公式G称为可满足公式(satisfiable),如果它不是永假的
G 是永真的当且仅当 ¬G 是永假的;
G 是可满足的当且仅当至少有一个解释 I,使 G 在 I 下为真。
永真式一定是可满足式,但反之可满足公式不一定是永真式
2.5.2 公式的等价
定义
设 G,H 是两个命题公式,P1,P2,P3,· · · ,Pn是出现在 G,H 中所有的命题变元,如果对于P1,P2,P3,· · · ,Pn 的 2^n 个解释,G 与 H 的真值结果都相同,则称公式 G 与 H 是等价的,记作G = H。(或G ⇔ H)
2.5.3 公式等价的充分必要条件
对于任意两个公式 G 和 H,G = H 的充分必要条件是公式 G ↔ H 是永真公式。
证明
- 必要性:假定 G = H,则 G,H 在其任意解释 I 下或同为真或同为假,于是由 “↔” 的意义知,公式 G ↔ H 在其任何的解释 I 下,其真值为“真”,即 G ↔ H 为永真公式。
- 充分性:假定公式 G ↔ H 是永真公式,I 是它的任意解释,在 I 下,G ↔ H 为真,因此,G,H 或同为真,或同为假,由于 I 的任意性,故有 G = H。
2.5.4 命题公式的可判定性
可判定性: 能否给出一个可行方法,完成对任意公式的判定类问题。(类型或等价判定)命题公式是可判定的。
2.6 基本等价关系及其应用
2.6.1 基本等价关系
设 G, H, S 为任意的命题公式
幂等律
- G ∨ G = G
- G ∧ G = G
交换律
- G ∨ H = H ∨ G
- G ∧ H = H ∧ G
结合律
- G ∨ (H ∨ S) = (G ∨ H) ∨ S
- G ∧ (H ∧ S) = (G ∧ H) ∧ S
同一律
- G ∨ 0 = G
- G ∧ 1 = G
零律
- G ∨ 1 = 1
- G ∧ 0 = 0
分配律
- G ∨ (H ∧ S) = (G ∨ H) ∧ (G ∨ S)
- G ∧ (H ∨ S) = (G ∧ H) ∨ (G ∧ S)
吸收律
- G ∨ (G ∧ H) = G
- G ∧ (G ∨ H) = G
矛盾律
- ¬G ∧ G = 0
排中律
- ¬G ∨ G = 1
双重否定律
- ¬(¬G) = G
德摩根律
- ¬(G ∨ H) = ¬G ∧ ¬H
- ¬(G ∧ H) = ¬G ∨ ¬H
蕴涵式
- G → H = ¬G ∨ H
假言易位
- G → H = ¬H → ¬G
等价式
- G ↔ H = (G → H) ∧ (H → G) = (¬G ∨ H) ∧ (¬H ∨ G)
等价否定等式
- G ↔ H = ¬G ↔ ¬H
归谬论
- (G → H) ∧ (G → ¬H) = ¬G
2.6.2 判断公式类型
利用命题公式的基本等价关系,证明 (P → Q) ∧ P → Q 是重言式。
证明
(P → Q) ∧ P → Q
= (¬P ∨ Q) ∧ P → Q = ¬((¬P ∨ Q) ∧ P) ∨ Q (蕴含式)
= (¬(¬P ∨ Q) ∨ ¬P) ∨ Q = ((P ∧ ¬Q) ∨ ¬P) ∨ Q (德摩根律)
= ((P ∨ ¬P) ∧ (¬Q ∨ ¬P)) ∨ Q (分配律)
= (1 ∧ (¬Q ∨ ¬P)) ∨ Q (排中律)
= (¬Q ∨ ¬P) ∨ Q (同一律)
= (¬Q ∨ Q) ∨ ¬P (结合律,交换律)
= 1 ∨ ¬P (排中律)
= 1 (零律)
2.6.3 证明公式等价
利用命题公式的基本等价关系,证明 P → (Q → R) = (P ∧ Q) → R。
证明
P → (Q → R)
= ¬P ∨ (Q → R) (蕴含式)
= ¬P ∨ (¬Q ∨ R) (蕴含式)
= (¬P ∨ ¬Q) ∨ R (结合律)
= ¬(P ∧ Q) ∨ R (德摩根律)
= (P ∧ Q) → R (蕴含式)
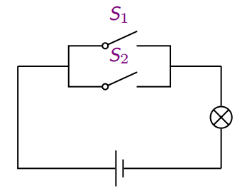
2.6.4 开关电路化简
利用命题公式的基本等价关系,化简如下图所示开关电路
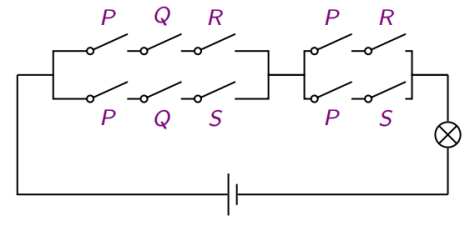
((P ∧ Q ∧ R) ∨ (P ∧ Q ∧ S)) ∧ ((P ∧ R) ∨ (P ∧ S))
= (P ∧ Q ∧ (R ∨ S)) ∧ (P ∧ (R ∨ S))
= P ∧ Q ∧ (R ∨ S) ∧ P ∧ (R ∨ S)
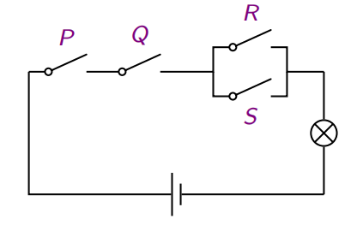
= P ∧ Q ∧ (R ∨ S)
因此简化为如下电路
2.6.5 逻辑电路化简
利用命题公式的基本等价关系,化简下图所示逻辑电路
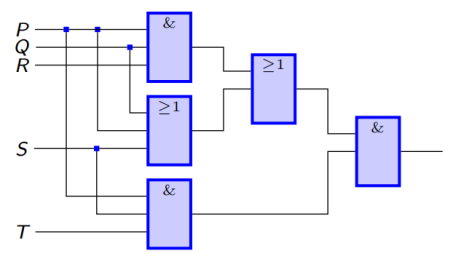
((P ∧ Q ∧ R) ∨ (P ∨ Q ∨ S)) ∧ (P ∧ S ∧ T)
= (P ∨ Q ∨ S) ∧ (P ∧ S ∧ T)
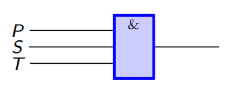
= P ∧ S ∧ T
因此,可简化为如下电路
2.6.6 解决推理问题
侦探调查了罪案的四位证人。从证人的话侦探得出的结论是:
- 如果男管家说的是真话,那么厨师说的也是真话;
- 厨师和园丁说的不可能都是真话;
- 园丁和杂役不可能都在说谎;
- 如果杂役说真话,那么厨师在说谎。
侦探能判定这四位证人分别是在说谎还是在说真话吗?解释你的推理。
解 令命题 P: 男管家说的是真话;Q:厨师说的是真话;R:园丁说的是真话;
S:杂役说的是真话。则将上述已知条件符号化并列出真值表,选取真值结果全为真的行如下表:
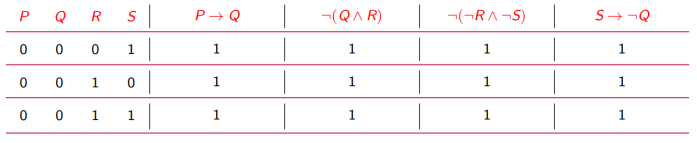
可见,我们能确定 P,Q 必然为假,但无法确定 R 和 S 的值,因而侦探只能判定男管家和厨师在说谎,但无法判定园丁与杂役谁在说真话。





![[附源码]java毕业设计美妆销售系统](https://img-blog.csdnimg.cn/05de159d485f409e83fb460473fe9d57.png)
![[附源码]java毕业设计农产品网络销售系统](https://img-blog.csdnimg.cn/dfabc9552358486d9383f05b81152596.png)