Minimum Spanning Tree

两大算法：Kruskal 与 Prim

树的含义：

• 结构中不能形成环

• 必须连接图结构中的全部顶带，任意两个顶点都是互通的

不同的生成树有不同的权值和，而最小生成树即为最小的那个树

如何构造最小生成树

**目标：**权值和达到最小值

每一步优先选择权值最小的边

Kruskal：直接选择权值最小的边

Prim：从顶点出发，间接选择与顶点相连权值最小的边

Kruskal Algorithm

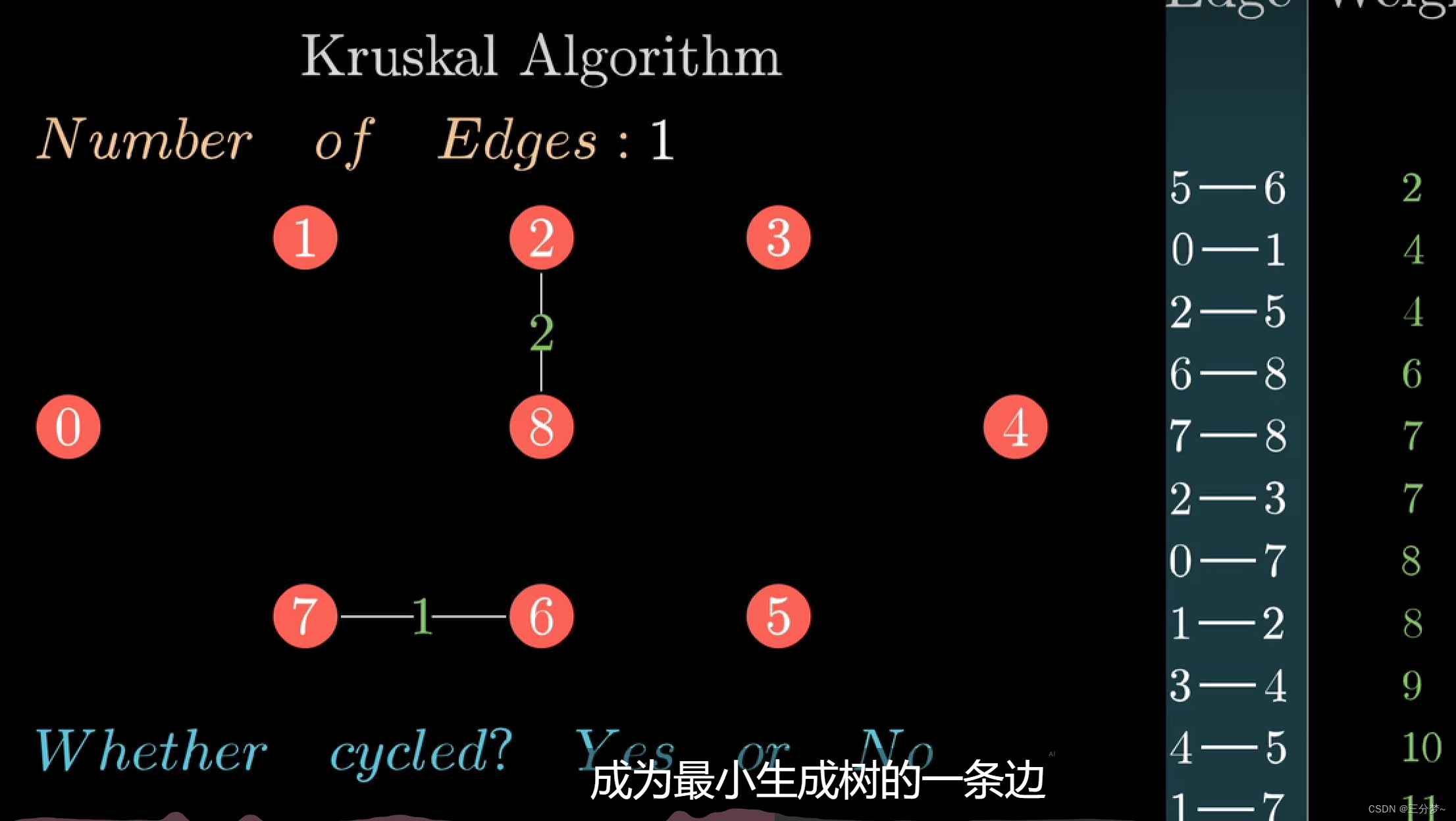
1. 将图中所有边取出，放入一个列表，并按照边取值按从小到大的顺序重新排列

2. 回填，从列表中按照次序每次取出一条边，回填到图中

3. 每次回填到图中时，进行判断图中是否形成环

   1. 若没有出现环，则选中此条边
   2. 若出现环，那么丢弃此边，选择下条边进行遍历判断

4. 直到已经选了n - 1条边，构建完成

---

Prim Algorithm

问题引入

有8个城市，他们的距离各不相同，假如在他们之间铺设铁路，要怎么才能使得费用最小呢

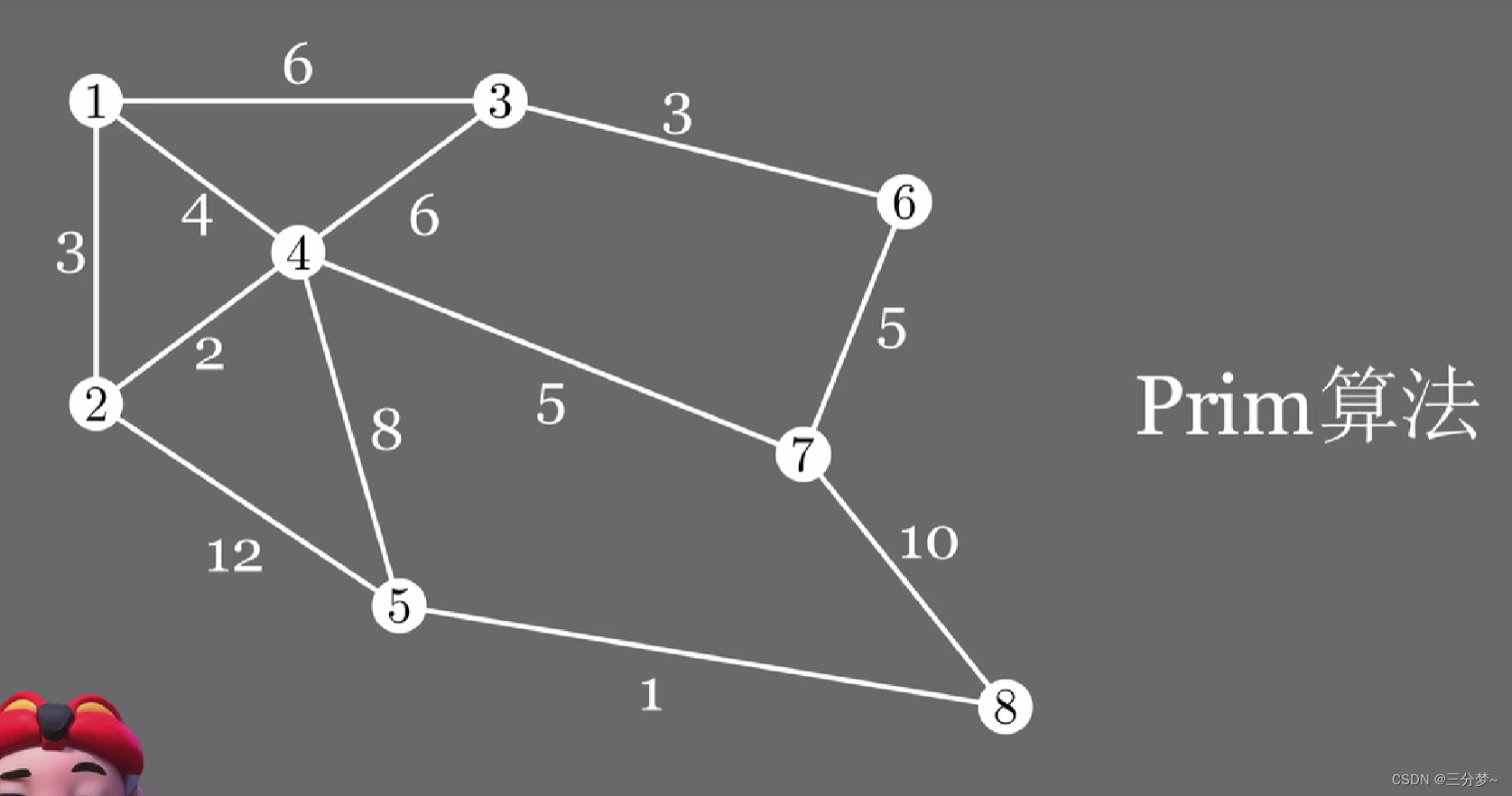
• 首先选择一个起始点，选择相连的权值最小的边
• 把选择的城市加入选定城市集合中
• 接着观察所有选定城市的边，再次选择权值最小的边
• 直到所有城市都被加入进选定城市集合中，算法结束

相关例题

Prim Algorithm

https://www.acwing.com/problem/content/860/

题目如下：

完整代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int g[N][N];    //存储图，g[i][j]，从i到j的距离
int dist[N];    //存储某个节点到选定集合的最短距离
bool st[N]; //判断是否在选定集合
int n, m;

void prim() {
    memset(dist, 0x3f3f3f3f, sizeof dist);
    dist[1] = 0;//从1号节点开始生成
    int res = 0;    //权重和
    for(int i = 0; i < n; i++) {    //每次循环选出一个点加入到选定集合中
        int t = -1;
        for(int j = 1; j <= n; j++) {   //对每个节点进行判断
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;  //找到距离最小的t
        }
        
        if(dist[t] == 0x3f3f3f3f) {   //若最小的为无穷，那么这块肯定短路，走不通
            printf("impossible");   //这里因为边权可能为负数
            return;
        }
        //else 
        st[t] = true;   //合理则选定t
        res += dist[t]; //更新答案
        for(int j = 1; j <= n; j++) {   //与最短点t相连的边
            if(!st[j]) {//从 t 到节点 i 的距离小于原来距离，则更新。
                dist[j] = min(dist[j], g[t][j]);  //更新dist[j]
            }
        }
    }
    cout << res;
}

int main() {
    memset(g, 0x3f3f3f3f, sizeof g);
    cin >> n >> m;
    while(m --) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        g[a][b] = g[b][a] = min(w, g[a][b]);    //存储权重，去重边
    }
    prim();
    
    return 0;
}

Kruskal Algorithm

https://www.acwing.com/problem/content/861/

题目如下：

思路分析

完整代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 200010, INF = 0x3f3f3f3f;
int n, m;
int p[N];
struct Edge{
    int a, b, w;
    bool operator< (const Edge &W)const {
        return w < W.w;
    }
}edges[N];

int find(int x) {   //并查集的操作
    if(p[x] != x)   p[x] = find(p[x]);
    return p[x];
}

int kruskal() {
    sort(edges, edges + m); //先进行排序，然后进行查找
    for(int i = 1; i <= n; i++) p[i] = i;   //并查集初始化
    int res = 0, cnt = 0;
    for(int i = 0; i < m; i++) {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);
        if(a != b) {    //若不连通，那么连通，并加入集合
            p[a] = b;
            res += w;
            cnt++;
        }
    }
    if(cnt < n - 1) res = INF;
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    for(int i = 0; i < m; i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }
    int t = kruskal();
    if(t == INF)  puts("impossible");
    else printf("%d\n", t);
    
    return 0;
}