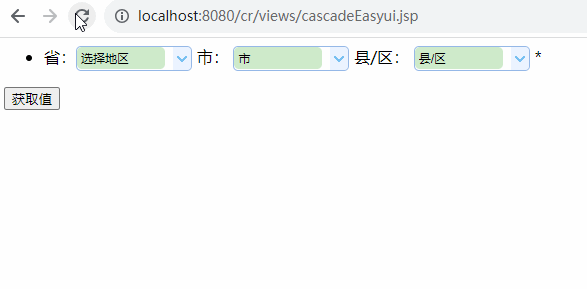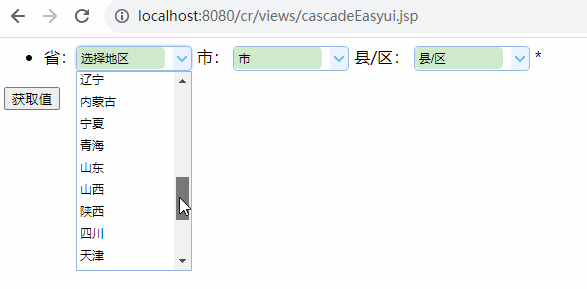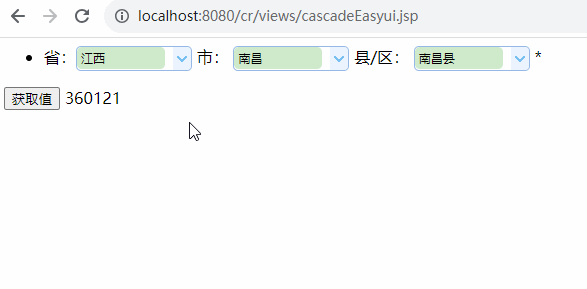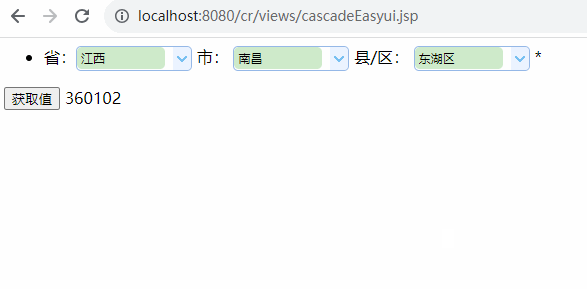
1 文本格式

// C++ Version
long long binpow(long long a, long long b) {
    if (b == 0) return 1;
    long long res = binpow(a, b / 2);
    if (b % 2)
        return res * res * a;
    else
        return res * res;
}

// C++ Version
long long binpow(long long a, long long b) {
    long long res = 1;
    while (b > 0) {
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
    }
    return res;
}

// C++ Version
long long binpow(long long a, long long b, long long m) {
    a %= m;
    long long res = 1;
    while (b > 0) {
        if (b & 1) res = res * a % m;
        a = a * a % m;
        b >>= 1;
    }
    return res;
}

#include <bits/stdc++.h>
using namespace std;
int a[505], b[505], t[505], i, j;

int mult(int x[], int y[])  // 高精度乘法
{
    memset(t, 0, sizeof(t));
    for (i = 1; i <= x[0]; i++) {
        for (j = 1; j <= y[0]; j++) {
            if (i + j - 1 > 100) continue;
            t[i + j - 1] += x[i] * y[j];
            t[i + j] += t[i + j - 1] / 10;
            t[i + j - 1] %= 10;
            t[0] = i + j;
        }
    }
    memcpy(b, t, sizeof(b));
}

void ksm(int p)  // 快速幂
{
    if (p == 1) {
        memcpy(b, a, sizeof(b));
        return;
    }
    ksm(p / 2);  //(2^(p/2))^2=2^p
    mult(b, b);  // 对b平方
    if (p % 2 == 1) mult(b, a);
}

int main() {
    int p;
    scanf("%d", &p);
    a[0] = 1;  // 记录a数组的位数
    a[1] = 2;  // 对2进行平方
    b[0] = 1;  // 记录b数组的位数
    b[1] = 1;  // 答案数组
    ksm(p);
    for (i = 100; i >= 1; i--) {
        if (i == 1) {
            printf("%d\n", b[i] - 1);  // 最后一位减1
        }
        else
            printf("%d", b[i]);
    }
}
 

2 代码格式

// C++ Version
long long binpow(long long a, long long b) {
    if (b == 0) return 1;
    long long res = binpow(a, b / 2);
    if (b % 2)
        return res * res * a;
    else
        return res * res;
}

// C++ Version
long long binpow(long long a, long long b) {
    long long res = 1;
    while (b > 0) {
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
    }
    return res;
}

// C++ Version
long long binpow(long long a, long long b, long long m) {
    a %= m;
    long long res = 1;
    while (b > 0) {
        if (b & 1) res = res * a % m;
        a = a * a % m;
        b >>= 1;
    }
    return res;
}

数组算法（抄的，忘了原作者，致歉）

#include <bits/stdc++.h>
using namespace std;
int a[505], b[505], t[505], i, j;

int mult(int x[], int y[])  // 高精度乘法
{
    memset(t, 0, sizeof(t));
    for (i = 1; i <= x[0]; i++) {
        for (j = 1; j <= y[0]; j++) {
            if (i + j - 1 > 100) continue;
            t[i + j - 1] += x[i] * y[j];
            t[i + j] += t[i + j - 1] / 10;
            t[i + j - 1] %= 10;
            t[0] = i + j;
        }
    }
    memcpy(b, t, sizeof(b));
}

void ksm(int p)  // 快速幂
{
    if (p == 1) {
        memcpy(b, a, sizeof(b));
        return;
    }
    ksm(p / 2);  //(2^(p/2))^2=2^p
    mult(b, b);  // 对b平方
    if (p % 2 == 1) mult(b, a);
}

int main() {
    int p;
    scanf("%d", &p);
    a[0] = 1;  // 记录a数组的位数
    a[1] = 2;  // 对2进行平方
    b[0] = 1;  // 记录b数组的位数
    b[1] = 1;  // 答案数组
    ksm(p);
    for (i = 100; i >= 1; i--) {
        if (i == 1) {
            printf("%d\n", b[i] - 1);  // 最后一位减1
        }
        else
            printf("%d", b[i]);
    }
}