神经网络 模型表示
模型表示一
为了构建神经网络模型,我们需要首先思考大脑中的神经网络是怎样的?每一个神经元都可以被认为是一个处理单元/神经核(processing unit/Nucleus),它含有许多输入/树突(input/Dendrite),并且有一个输出/轴突(output/Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
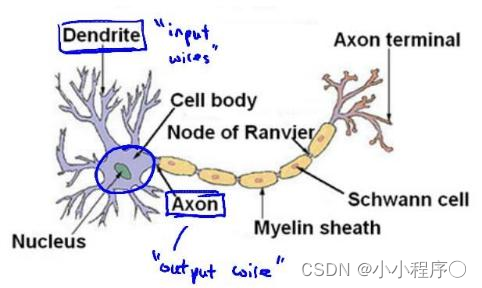
下面是一组神经元的示意图,神经元利用微弱的电流进行沟通。这些弱电流也称作动作电位,其实就是一些微弱的电流。所以如果神经元想要传递一个消息,它就会就通过它的轴突,发送一段微弱电流给其他神经元,这就是轴突。
这里是一条连接到输入神经,或者连接另一个神经元树突的神经,接下来这个神经元接收这条消息,做一些计算,它有可能会反过来将在轴突上的自己的消息传给其他神经元。这就是所有人类思考的模型:我们的神经元把自己的收到的消息进行计算,并向其他神经元传递消息。这也是我们的感觉和肌肉运转的原理。如果你想活动一块肌肉,就会触发一个神经元给你的肌肉发送脉冲,并引起你的肌肉收缩。如果一些感官:比如说眼睛想要给大脑传递一个消息,那么它就像这样发送电脉冲给大脑的。
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被成为权重(weight)。

我们设计出了类似于神经元的神经网络,效果如下:
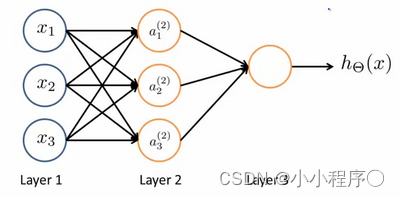
其中
x
1
x_1
x1,
x
2
x_2
x2,
x
3
x_3
x3是输入单元(input units),我们将原始数据输入给它们。
a
1
a_1
a1,
a
2
a_2
a2,
a
3
a_3
a3是中间单元,它们负责将数据进行处理,然后呈递到下一层。
最后是输出单元,它负责计算
h
θ
(
x
)
{h_\theta}\left( x \right)
hθ(x)。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit)
下面引入一些标记法来帮助描述模型:
a
i
(
j
)
a_{i}^{\left( j \right)}
ai(j) 代表第
j
j
j 层的第
i
i
i 个激活单元。
θ
(
j
)
{{\theta }^{\left( j \right)}}
θ(j)代表从第
j
j
j 层映射到第$ j+1$ 层时的权重的矩阵,例如
θ
(
1
)
{{\theta }^{\left( 1 \right)}}
θ(1)代表从第一层映射到第二层的权重的矩阵。其尺寸为:以第
j
+
1
j+1
j+1层的激活单元数量为行数,以第
j
j
j 层的激活单元数加一为列数的矩阵。例如:上图所示的神经网络中
θ
(
1
)
{{\theta }^{\left( 1 \right)}}
θ(1)的尺寸为 3*4。
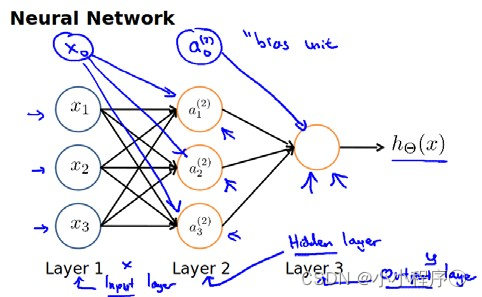
对于上图所示的模型,激活单元和输出分别表达为:
a
1
(
2
)
=
g
(
Θ
10
(
1
)
x
0
+
Θ
11
(
1
)
x
1
+
Θ
12
(
1
)
x
2
+
Θ
13
(
1
)
x
3
)
a_{1}^{(2)}=g(\Theta _{10}^{(1)}{{x}_{0}}+\Theta _{11}^{(1)}{{x}_{1}}+\Theta _{12}^{(1)}{{x}_{2}}+\Theta _{13}^{(1)}{{x}_{3}})
a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a
2
(
2
)
=
g
(
Θ
20
(
1
)
x
0
+
Θ
21
(
1
)
x
1
+
Θ
22
(
1
)
x
2
+
Θ
23
(
1
)
x
3
)
a_{2}^{(2)}=g(\Theta _{20}^{(1)}{{x}_{0}}+\Theta _{21}^{(1)}{{x}_{1}}+\Theta _{22}^{(1)}{{x}_{2}}+\Theta _{23}^{(1)}{{x}_{3}})
a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a
3
(
2
)
=
g
(
Θ
30
(
1
)
x
0
+
Θ
31
(
1
)
x
1
+
Θ
32
(
1
)
x
2
+
Θ
33
(
1
)
x
3
)
a_{3}^{(2)}=g(\Theta _{30}^{(1)}{{x}_{0}}+\Theta _{31}^{(1)}{{x}_{1}}+\Theta _{32}^{(1)}{{x}_{2}}+\Theta _{33}^{(1)}{{x}_{3}})
a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
h
Θ
(
x
)
=
g
(
Θ
10
(
2
)
a
0
(
2
)
+
Θ
11
(
2
)
a
1
(
2
)
+
Θ
12
(
2
)
a
2
(
2
)
+
Θ
13
(
2
)
a
3
(
2
)
)
{{h}_{\Theta }}(x)=g(\Theta _{10}^{(2)}a_{0}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}+\Theta _{13}^{(2)}a_{3}^{(2)})
hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
上面进行的讨论中只是将特征矩阵中的一行(一个训练实例)喂给了神经网络,我们需要将整个训练集都喂给我们的神经网络算法来学习模型。
我们可以知道:每一个 a a a都是由上一层所有的 x x x和每一个 x x x所对应的决定的。
(我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION ))
把
x
x
x,
θ
\theta
θ,
a
a
a 分别用矩阵表示:
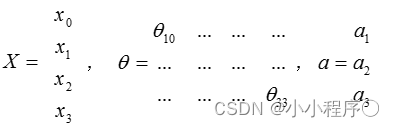
我们可以得到 θ ⋅ X = a \theta \cdot X=a θ⋅X=a 。