1.算法描述

禁忌搜索（Tabu Search或Taboo Search，简称TS）是对局部搜索（LS）的一种扩展，是一种全局寻优算法，其特点是采用禁忌技术，即用一个禁忌表记录下已经到达过的局部最优点及求解过程，在下一次搜索中，利用禁忌表中的信息不再或有选择地搜索这些点，以此来跳出局部最优点。该算法可以克服爬山算法全局搜索能力不强的弱点。

禁忌搜索(Tabu Search，TS )也是一种模拟人类智能的优化算法。

上图涉及禁忌搜索的一些基本概念，现在我们来讨论这些概念。

禁忌表（Tabu List，TL）

这是用于保管(记忆)禁忌对象的表。是进行禁忌搜索的基本前提。禁忌表本身有容量限制，其大小会影响禁忌对象的存储个数，影响算法的性能。

禁忌对象（Tabu Object，TO）

是指禁忌表中禁止的变化要素。禁忌对象的选择可以根据具体问题确定。例如，旅行者问题(Traveling Salesman Problem，TSP ) )可以禁忌被交换的城市对，也可以禁忌总路径长度。

禁忌期限（Tabu Tenure，TT）

也称为禁忌长，是指禁忌对象未被选择的周期。禁忌期过短容易发生循环，难以跳出局部最佳，过长会增加计算时间。

渴望准则（Aspiration Criteria，AC）

也称为特赦规则。所有对象被禁忌后，可以解禁其中性能最好的对象，也可以在解禁某个对象能带来目标值大幅改善的情况下使用特赦规则。

1.2 基本流程

禁忌搜索算法在初始化时，在搜索空间中随机生成初始解I、禁忌表H 置空，将当前解I记录为历史最优解s，进入迭代搜索过程。对于每次迭代，从当前解I开始，在当前禁忌表h的限制下，构造解I的邻域A，从a中选出适应值最好的解j替换解I，同时http://www 否则，s保持不变，即使解I暂时变差，也有利于通过扩大搜索空间来摆脱局部最优。在获得新的当前解I之后，该算法返回开始迭代，并且在找到最佳解或已经执行更新(例如，一定的迭代次数)时结束该算法。

禁忌搜索算法的一般流程如下：

（1）初始化TS算法的参数，按照准则生成问题的初始解，生成0禁忌表；

（2）判断是否满足终止条件，若是，则结束算法，输出结果

（3）根据算法的特性生成领域解，并从中选择合适规模大小的候选解；

（4）判断候选解中的最优解Next是否满足特赦准则，若满足特赦准则，则用Next替代当前最优解Before，并更新禁忌表，令Next对应的禁忌对象的禁忌长度为最长，即禁忌时间最长；若不满足特赦准则，进行（4）步骤；

（5）判断候选解中禁忌状态情况，找出候选解中处于“非禁忌”状态的禁忌对象，并把该禁忌对象对应的解赋给当前最优解，同时设置该禁忌对象的禁忌时间为最长；

（6）转（2）；

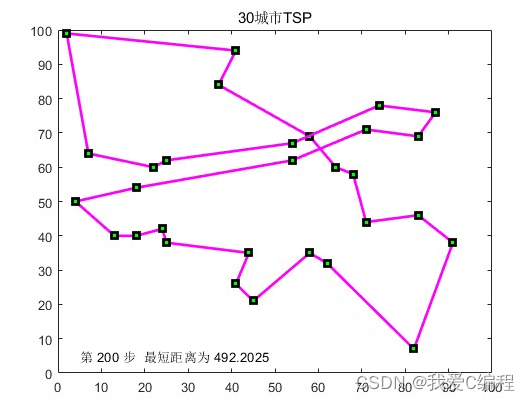
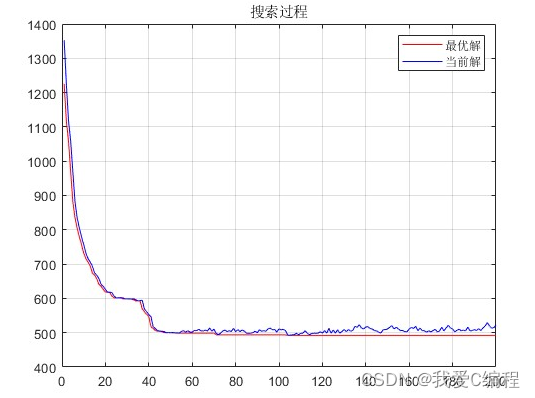
2.仿真效果预览

matlab2022a仿真结果如下：

3.MATLAB核心程序

.......................
Tlist=zeros(CityNum);%禁忌表(tabu list)
cl=100;%保留前cl个最好候选解
bsf=Inf;
tl=50; %禁忌长度(tabu length)
l1=200;%候选解(candidate),不大于n*(n-1)/2(全部领域解个数)
S0=randperm(CityNum);
S=S0;
BSF=S0;
Si=zeros(l1,CityNum);
StopL=200; %终止步数
p=1;
clf;
figure(1);
 
while (p<StopL+1)
    if l1>CityNum*(CityNum)/2
        disp('候选解个数,不大于n*(n-1)/2(全部领域解个数)！ 系统自动退出！');
        l1=(CityNum*(CityNum)/2)^.5;
        break;
    end
    ArrS(p)=CalDist(dislist,S);        
    i=1;
    A=zeros(l1,2);
    while i<=l1        
        M=CityNum*rand(1,2);
        M=ceil(M);
        if M(1)~=M(2)
            m1=max(M(1),M(2));m2=min(M(1),M(2));
            A(i,1)=m1;A(i,2)=m2;
            if i==1
                isdel=0;
            else
                for j=1:i-1
                    if A(i,1)==A(j,1)&&A(i,2)==A(j,2)
                        isdel=1;
                        break;
                    else
                        isdel=0;
                    end
                end
            end
            if ~isdel
                i=i+1;
            else
                i=i;
            end
        else 
            i=i;
        end
    end
    
    for i=1:l1
        Si(i,:)=S;
        Si(i,[A(i,1),A(i,2)])=S([A(i,2),A(i,1)]);
        CCL(i,1)=i;
        CCL(i,2)=CalDist(dislist,Si(i,:));
        CCL(i,3)=S(A(i,1));
        CCL(i,4)=S(A(i,2));   
    end
    [fs fin]=sort(CCL(:,2));
    for i=1:cl
        CL(i,:)=CCL(fin(i),:);
    end
    
    if CL(1,2)<bsf  %藐视准则(aspiration criterion)
        bsf=CL(1,2);
        S=Si(CL(1,1),:);        
        BSF=S;
        for m=1:CityNum
            for n=1:CityNum
                if Tlist(m,n)~=0
                    Tlist(m,n)=Tlist(m,n)-1;
                end
            end
        end
        Tlist(CL(1,3),CL(1,4))=tl;
    else  
        for i=1:cl
            if Tlist(CL(i,3),CL(i,4))==0
                S=Si(CL(i,1),:);
                for m=1:CityNum
                    for n=1:CityNum
                        if Tlist(m,n)~=0
                            Tlist(m,n)=Tlist(m,n)-1;
                        end
                    end
                end
                Tlist(CL(i,3),CL(i,4))=tl;
                break;
            end
        end
    end
    
    Arrbsf(p)=bsf;
    drawTSP(Clist,BSF,bsf,p,0);
    p=p+1;
end
BestShortcut=BSF
theMinDistance=bsf
...................................
A136