文章目录
- 数组中重复的数字
- 题目
- 思路
- 代码
- 在排序数组中查找数据
- 题目
- 思路
- 代码
- 0~n-1中缺失的数字
- 题目
- 思路
- 代码
数组中重复的数字
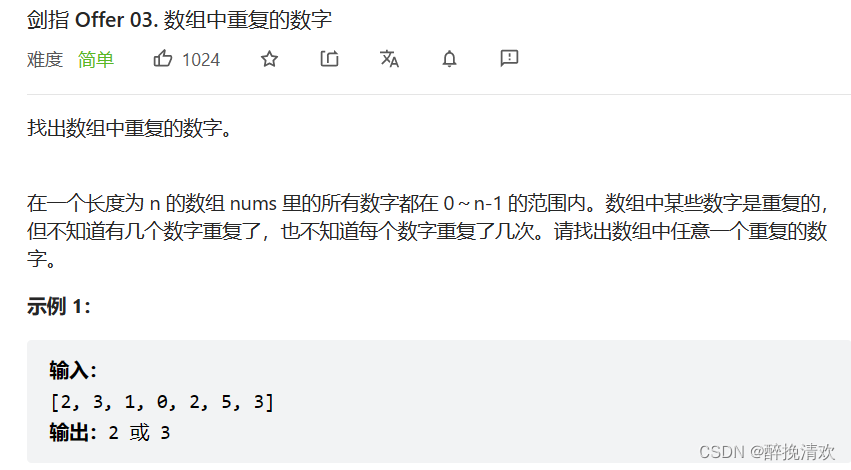
题目
思路
创建一个哈希表,将数组遍历,如果不存在则添加到哈希表中,如果存在则直接返回
代码
var findRepeatNumber = function(nums) {
let map = new Map();
for(let i=0;i<nums.length;i++)
{
if(!map.has(nums[i]))
{
map.set(nums[i],i)
}else{
return nums[i]
}
}
return null
};
在排序数组中查找数据
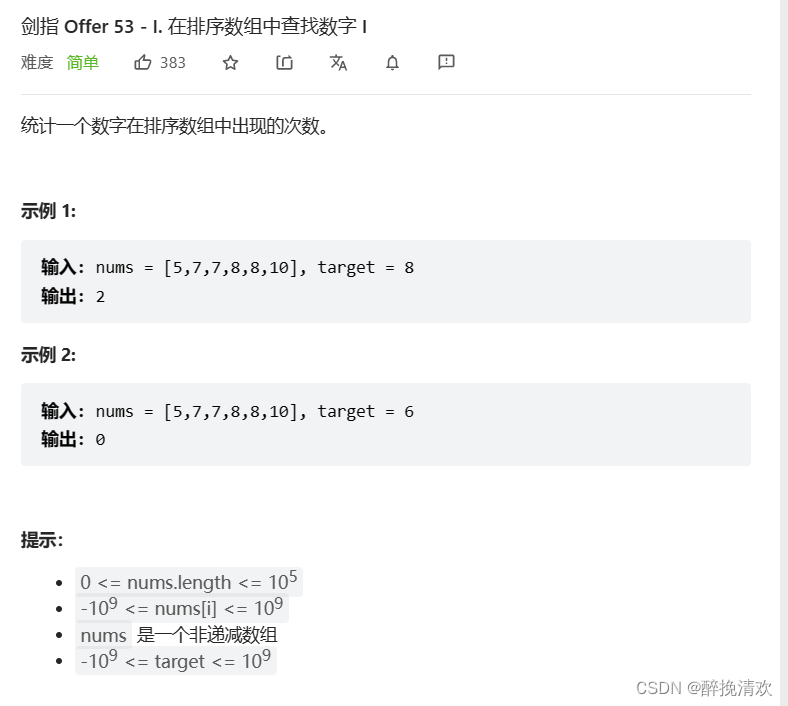
题目
思路
定义targetLeft 和 targetRight为等于目标值的最两边的下表,然后利用二分查找来得到targetLeft 和 targetRight,最后两者相减加1就是结果;
计算targetLeft 的步骤如下:
- 首先定义targetLeft为一个随便的值,如-1;定义左右指针,分别指向数组的第一个元素个最后一个元素

- 接着计算出中间指针mid,如图为2,判断nums[2]=7<target

- 接着令left=mid+1

- 再计算mid=4,同时nums[4]==target

- targetLeft=mid

- right=mid-1

- 此时left=right,所以还要继续循环,计算mid=3,同时nums[3]=target

- 所以令targetLeft=mid=3
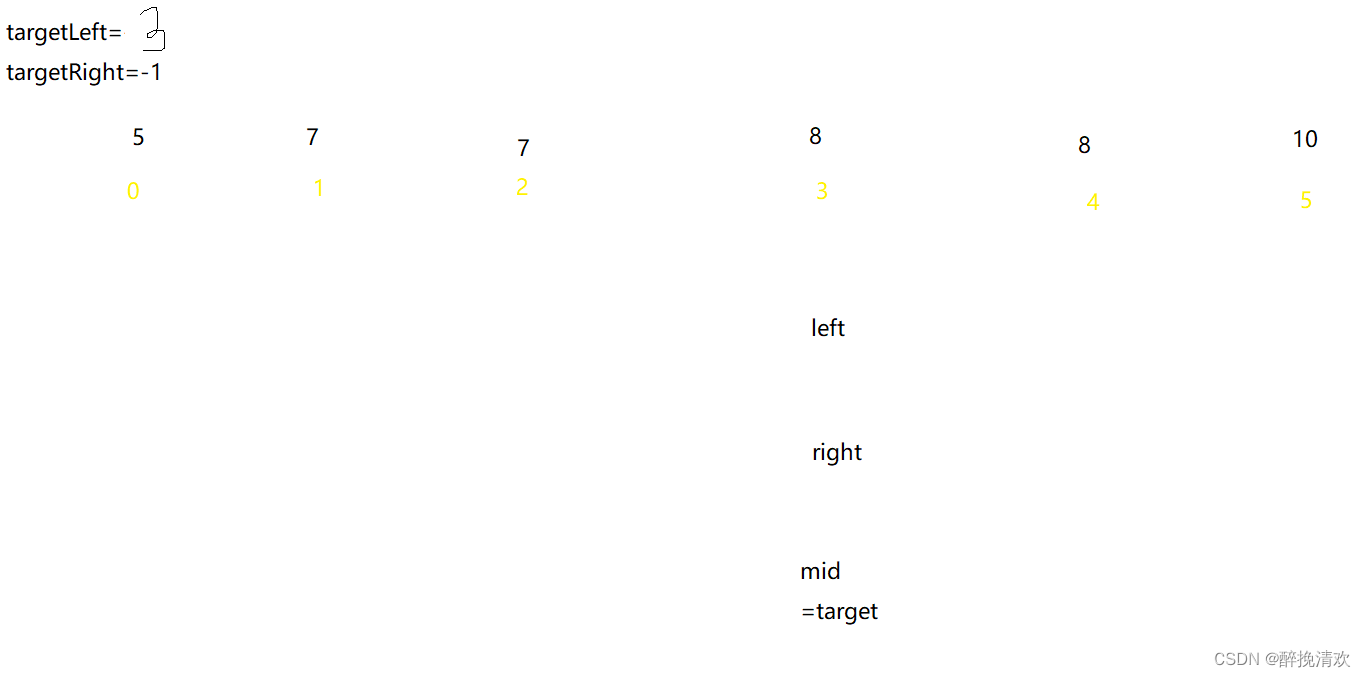
- 令right=mid-1,此时right<left,跳出循环。

求targetRight的步骤也是一样。
代码
var search = function (nums, target) {
var targetLeft = -1,
targetRight = -1,
left=0,
right=nums.length-1;
//找出该数在左边第一次出现的位置
while (left<=right) {
var mid = Math.floor((left + right) / 2);
if (target == nums[mid]) {
targetLeft = mid; //记录下第一次出现的下标
right=mid - 1; //继续向前查找是否该数出现过
} else if (target < nums[mid]) {
right = mid -1;
} else {
left = mid + 1;
}
}
//重置 left 和 right 的值,找出该数在右边最后一个出现的位置
left = 0;
right = nums.length - 1;
while (left <= right) {
var mid = Math.floor((left + right) / 2);
if (target == nums[mid]) {
targetRight = mid;
left = mid + 1;
} else if (target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return targetLeft<=targetRight&&targetLeft!==-1 ? targetRight - targetLeft + 1 : 0;
};
0~n-1中缺失的数字
题目
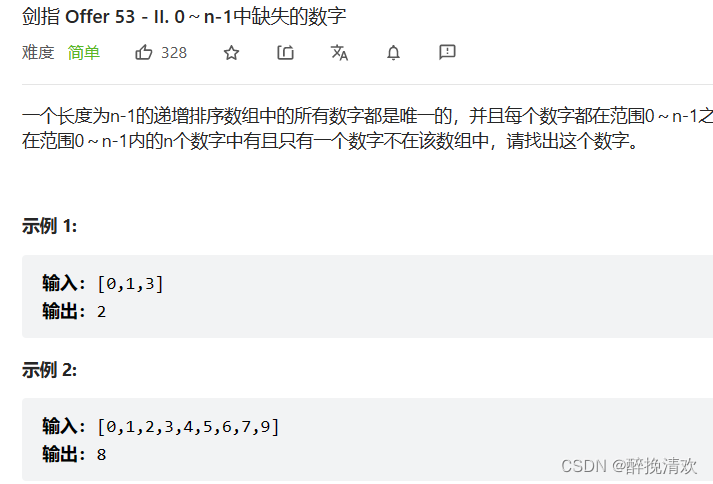
思路
利用数学公式计算出0-n的和,然后减去nums的和,就得到缺的数字了。
代码
var missingNumber = function(nums) {
const n = nums.length + 1;
let total = Math.floor(n * (n - 1) / 2);
let arrSum = 0;
for (let i = 0; i < n - 1; i++) {
arrSum += nums[i];
}
return total - arrSum;
};