目录

描述

输入描述：

输出描述：

解题过程

提交代码

学习代码

代码一

收藏点

---

描述

一个 DNA 序列由 A/C/G/T 四个字母的排列组合组成。 G 和 C 的比例（定义为 GC-Ratio ）是序列中 G 和 C 两个字母的总的出现次数除以总的字母数目（也就是序列长度）。在基因工程中，这个比例非常重要。因为高的 GC-Ratio 可能是基因的起始点。

给定一个很长的 DNA 序列，以及限定的子串长度 N ，请帮助研究人员在给出的 DNA 序列中从左往右找出 GC-Ratio 最高且长度为 N 的第一个子串。

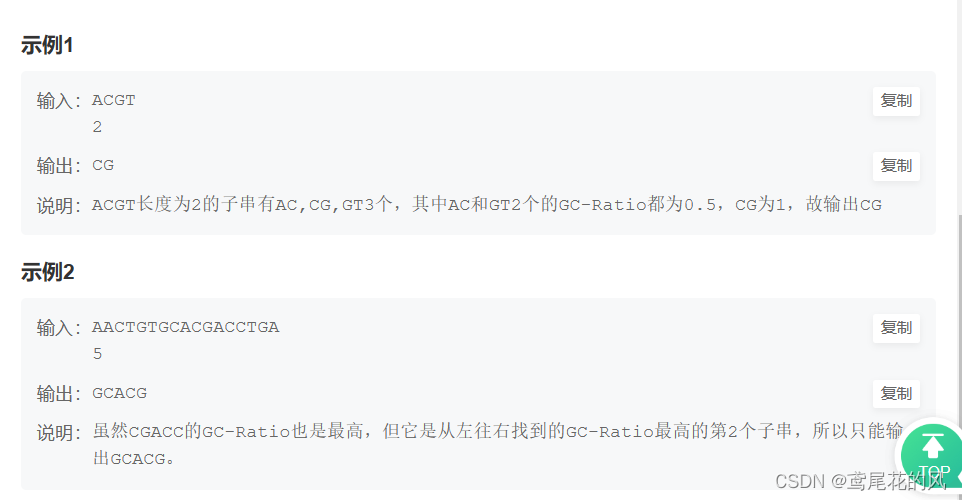
DNA序列为 ACGT 的子串有: ACG , CG , CGT 等等，但是没有 AGT ， CT 等等

数据范围：字符串长度满足 1≤n≤1000  ，输入的字符串只包含 A/C/G/T 字母

输入描述：

输入一个string型基因序列，和int型子串的长度

输出描述：

找出GC比例最高的子串,如果有多个则输出第一个的子串

解题过程

思路是这样滴：

1. 输入从i到strlen-1的一个字符串；

2. 设置一个滑动窗口，长度为N；

3. 设置一个字符串，长度为N；

4. 设置一个max=0，用来表示滑动窗口中，出现G||C的最大数目

5. 写一个for(i=0;i<strlen-N;i++)

{

        for(j=i;j<i+N;j++)//这是一个滑动窗口

                统计滑动窗口中C||G的数目count        

 if(count>max)

        {

                max=count;

                strcpy(第3步设置的长度为N的字符串, 滑动窗口)

         }

}

提交代码

学习代码

代码一

（来源：https://blog.nowcoder.net/n/830b65f9549c4848a4eea2158b533da0）

他的思路和我相近

#include<stdio.h>
#include<string.h>
int main()
{
    char str[1000];
    int n = 0;
    int max = 0;
    int flag = 0;
    scanf("%s", str);
    scanf("%d", &n);
    int len = strlen(str);
    for(int i=0; i<len-n; i++)
    {
        int cnt=0;
        for(int j=i; j<i+n; j++)
        {
            if(str[j] == 'G' || str[j] == 'C')
                 cnt++;
        }
        if(cnt > max)
        {
            max = cnt;
            flag = i;
        }
    }
    for(int k=flag; k<flag+n; k++)
    {
        printf("%c", str[k]);
    }
    return 0;
}

收藏点