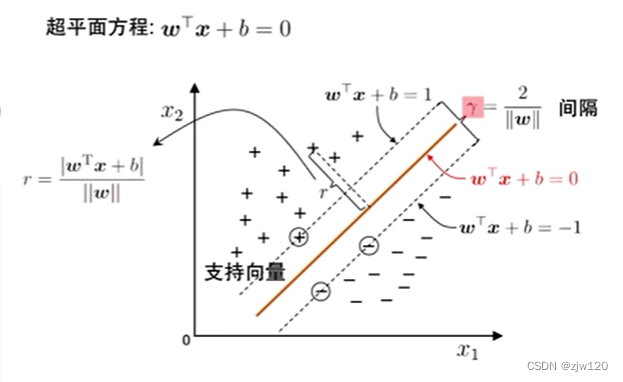
支持向量机
支持向量:距离超平面最近的这几个训练样本点。
支持向量机的核心思想是最大化间隔 γ = 2 ∣ ∣ w ∣ ∣ \gamma = \frac{2}{||w||} γ=∣∣w∣∣2。
求极大转换为求极小,转化为凸规划问题。
对偶问题
利用拉格朗日乘子法,对于不等式约束,在其前加入一个乘子 α i ≥ 0 \alpha_i \ge 0 αi≥0
支持向量机对偶问题得到的目标函数最优值是原始问题目标函数最优值的下界
KKT条件说明,要么 α i = 0 \alpha_i = 0 αi=0要么 y i f ˙ ( x i ) = 1 y_i \dot f(x_i)=1 yif˙(xi)=1。前者说明该点不会出现在解集内,即不符合约束;后者说明该点一定在支持向量上。因此,最终模型仅与支持向量有关。
求解方法—SMO
顺序性最小优化算法(sequential minimal optimization)
- 基本思路:按照KKT条件违背程度最大准则选取变量,固定一对变量 α i \alpha_i αi和 α j \alpha_j αj,对偶问题的约束为 0 = ∑ i = 1 m α i y i 0=\sum_{i=1}^{m} \alpha_i y_i 0=∑i=1mαiyi, 那么这对变量的和就固定了。接着用一个变量表示另一个变量,带入对偶问题的目标函数,求得闭式解。
- 循环重复1、2步骤,直至目标函数收敛。
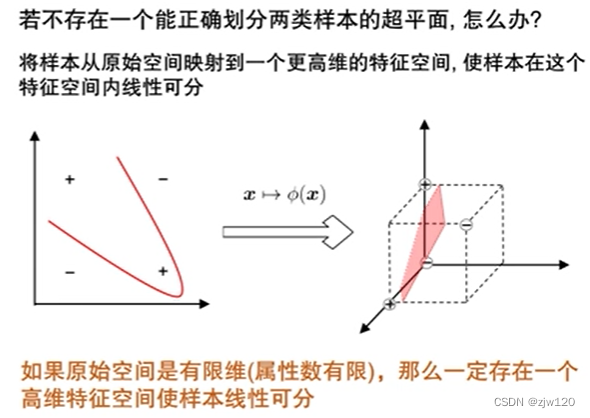
特征空间映射
将样本空间映射为高维空间(这个高维可以是无穷维),即将x映射为 ϕ ( x ) \phi (x) ϕ(x)
此时内积可以用核函数表示,能绕过显式考虑特征映射,直接在原始的特征空间计算,缓解计算高维内积的困难。
核函数
Mercer定理可以从点到点的距离数学表达理解。由于核函数的初衷是表示空间中两点的距离,因此对于对称核矩阵有:
| Ki | Kj | |
|---|---|---|
| Ki | (Ki,Ki) | (Ki,Kj) |
| Kj | (Kj,Ki) | (Kj,Kj) |
若对称轴上每一项均大于等于0,那么Ki和Kj两点之间的距离大于等于0.
d i s t ( x 1 , x 2 ) = ∥ ϕ ( x 1 ) − ϕ ( x 2 ) ∥ H k 2 = k ( x 1 , x 1 ) − 2 k ( x 1 , x 2 ) + k ( x 2 , x 2 ) dist(x_1,x_2)=\|\phi(x_1)-\phi(x_2)\|_{\mathcal{H}_k}^2=\sqrt{k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)} dist(x1,x2)=∥ϕ(x1)−ϕ(x2)∥Hk2=k(x1,x1)−2k(x1,x2)+k(x2,x2)对于两个样本点(0,0),(1,1),若我们将其投影到与高斯核函数
关联的RKHS中时,则两个样本投影后的点距离为1.315
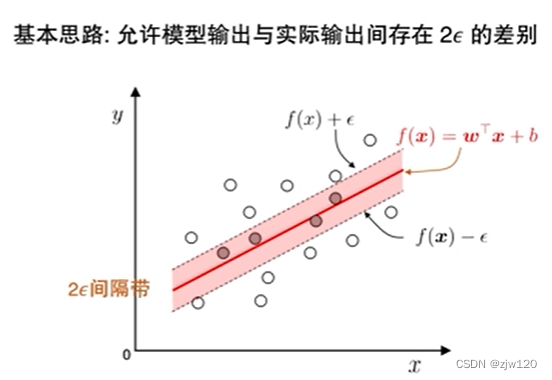
如何使用SVM
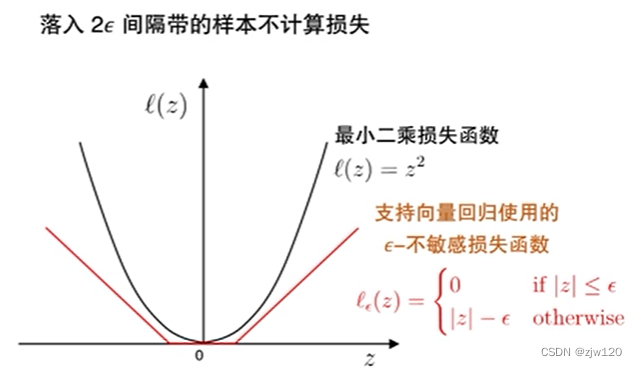
落在 2 ϵ 2\epsilon 2ϵ内不做惩罚,落在 2 ϵ 2\epsilon 2ϵ外部做惩罚;当样本距离超平面的距离大于一定程度时,有损失且损失随着距离线性增加;同时令所有损失加和最小。
间隔带两侧的松弛程度可有所不同,因此分别设定一个 ξ \xi ξ值。之后的计算同样使用拉格朗日乘子法即可。
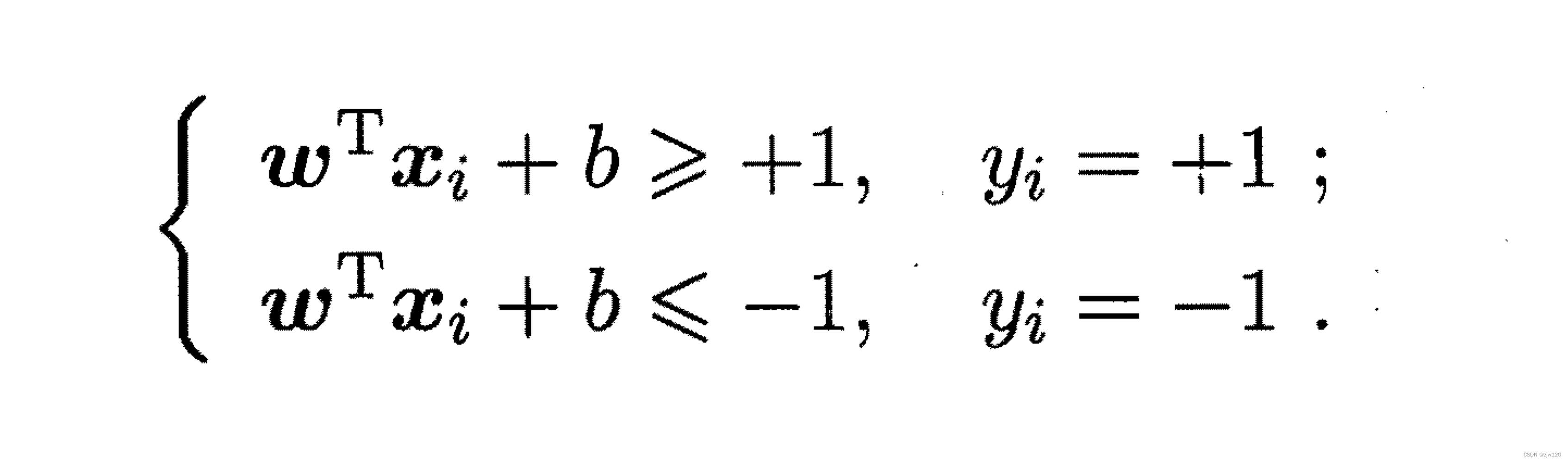






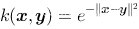



![第三章:远程登陆Linux系统-[实操篇]](https://img-blog.csdnimg.cn/e41c75379812420e906794b6b899ba76.png)