一、前言

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序，二叉搜索树将有可能退化为单支树，此时查找元素相当于在顺序表中查找元素，效率低下，时间复杂度接近O(n)。
最优情况下，二叉搜索树为完全二叉树。
最差情况下，二叉搜索树退化为单支树。

二、简介

AVL树是一颗自平衡的二叉树，是对BST的改进。每个节点均有一个平衡因子$p$（ $p=Height(T_L)-Height(T_R)$）。若每个节点的平衡因子的绝对值均小于等于1，则该树是AVL树。维护这种高度平衡所付出的代价也是很大的，故而实际应用并不多，因此更多的地方是用追求局部平衡而不是整体平衡的红黑树。

注：

1. AVL 树它的任何一个节点的左右子树都是 AVL 树。
2. AVL 树的查找、插入和删除在平均和最坏情况下都是O(logn)。

三、左旋与右旋

根据BTS树（二叉排序树）的性质，可以看出通过左旋和右旋操作后得到的树仍然是BTS树。

四、AVL树的调整

1、向AVL树中插入新数据

和BST一样，首先在叶节点插入数据。在 AVL 树中进行插入或删除节点后，可能导致 AVL 树失衡，需要对以插入路径上离插入节点最近的平衡因子绝对值大于1的节点为根的树进行调整。
这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)，RL(右左)。

1）LL型不平衡（右单旋转）

在某个子树的左子树的左子树上插入新节点，导致子树根节点的平衡因子由1变为2。

2）RR型不平衡（左单旋转）

在某个子树的左子树的左子树上插入新节点，导致子树根节点的平衡因子由-1变为-2。

3）LR型不平衡（左右双旋转）

在某个子树的左子树的右子树上插入新节点，导致子树根节点的平衡因子由1变为2。

感觉这里最不好理解，举一个较复杂的样例。其根本思想就是Z节点先进行左旋后进行右旋。
原AVL树：

插入节点11：

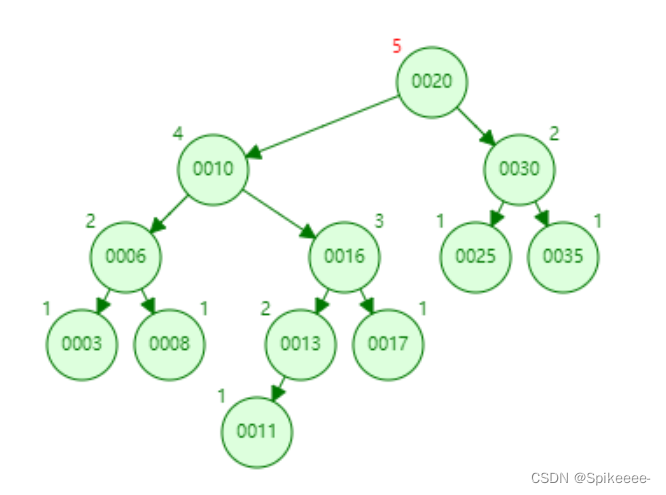
将节点16左旋右旋：

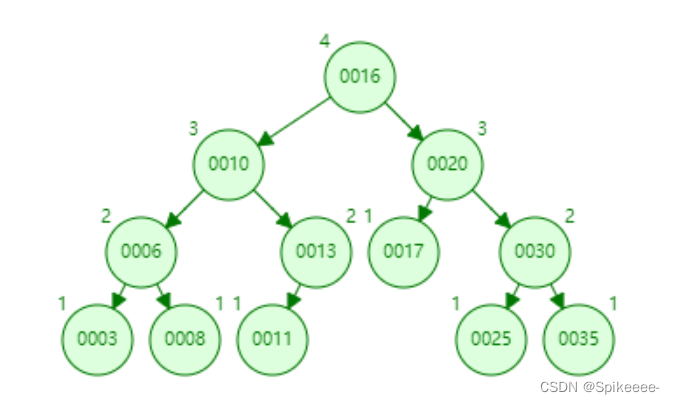
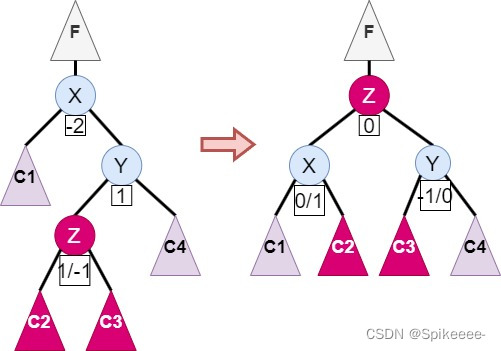
4）RL型不平衡（右左双旋转）

在某个子树的右子树的左子树上插入新节点，导致子树根节点的平衡因子由1变为2。

五、代码实现

#include <iostream>
#include <algorithm>

class AVL_Node
{
public:
    friend class AVL_Tree;
    AVL_Node() : _key(0), _cnt(0), _height(0), _lchild(0), _rchild(0) {}
    AVL_Node(int key) : _key(key), _cnt(0), _height(0), _lchild(0), _rchild(0) {}
    int height(AVL_Node *node)
    {
        if (!node)
            return -1;
        return node->_height;
    }
    void update_height()
    {
        _height = 1 + std::max(height(_lchild), height(_rchild));
    }
    int getBalenceFactor()
    {
        return height(_lchild) - height(_rchild);
    }
    void preorder(AVL_Node *node, std::ostream &os) const
    {
        if (node)
        {
            os << node->_key << " ";
            if (node->_lchild)
                preorder(node->_lchild, os);
            if (node->_rchild)
                preorder(node->_rchild, os);
        }
    }

private:
    int _key;
    int _cnt;
    int _height;
    AVL_Node *_lchild;
    AVL_Node *_rchild;
};

class AVL_Tree
{
public:
    AVL_Tree() : _root(0) {}
    AVL_Tree(AVL_Node *root) : _root(root) {}
    void insert(const int &);
    AVL_Node *insert_key(AVL_Node *node, const int &);
    AVL_Node *rightRotate(AVL_Node *Y)
    {
        /* 树结构示意图：
                Y
               / \
              X   O
             / \
            O   O
        */
        AVL_Node *X = Y->_lchild;
        AVL_Node *tmp = X->_rchild;
        X->_rchild = Y;
        Y->_lchild = tmp;
        Y->update_height();
        X->update_height();
        return X;
    }
    AVL_Node *leftRotate(AVL_Node *Y)
    {
        /* 树结构示意图：
                Y
               / \
              O   X
                 / \
                O   O
        */
        AVL_Node *X = Y->_rchild;
        AVL_Node *tmp = X->_lchild;
        X->_lchild = Y;
        Y->_rchild = tmp;
        Y->update_height();
        X->update_height();
        return X;
    }

    void preOrder();

private:
    AVL_Node *_root;
};

void AVL_Tree::insert(const int &key)
{
    if (!_root)
    {
        _root = new AVL_Node(key);
    }
    else
    {
        _root = insert_key(_root, key);
    }
}

AVL_Node *AVL_Tree::insert_key(AVL_Node *node, const int &key)
{
    if (key == node->_key)
    {
        ++(node->_cnt);
        return node;
    }

    if (key < node->_key)
    {
        if (!node->_lchild)
            node->_lchild = new AVL_Node(key);
        else
            node->_lchild = insert_key(node->_lchild, key);
    }
    else if (key > node->_key)
    {
        if (!node->_rchild)
            node->_rchild = new AVL_Node(key);
        else
            node->_rchild = insert_key(node->_rchild, key);
    }

    // 更新路径上每个节点的高度。
    node->update_height();
    // 计算平衡因子。
    int p = node->getBalenceFactor();

    // LL型不平衡。
    if (p > 1 && key < node->_lchild->_key)
    {
        return rightRotate(node);
    }
    // RR型不平衡。
    if (p < -1 && key > node->_rchild->_key)
    {
        return leftRotate(node);
    }
    // LR型不平衡。
    if (p > 1 && key > node->_lchild->_key)
    {
        node->_lchild = leftRotate(node->_lchild);
        return rightRotate(node);
    }
    // RL型不平衡。
    if (p < -1 && key < node->_rchild->_key)
    {
        node->_rchild = rightRotate(node->_rchild);
        return leftRotate(node);
    }
    return node;
}

void AVL_Tree::preOrder()
{
    std::cout << "preOrder: ";
    if (_root)
        _root->preorder(_root, std::cout);
    std::cout << std::endl;
}

int main()
{
    AVL_Tree* avl = new AVL_Tree();
    avl->insert(10);
    avl->insert(20);
    avl->insert(30);
    avl->insert(40);
    avl->insert(50);
    avl->insert(25);
    
    avl->preOrder();
}