值函数近似法
经典强化学习方法的共同点是它们的求解过程都要维持一个值函数表格,策略函数也可以通过一个表格来表示,所以也称这些方法为表格法。表格法要求状态空间和动作空间都是离散的,这类强化学习任务只占所有强化学习任务的很小一部分,大部分强化学习任务具有多维连续状态和动作空间,用经典强化学习方法很难求解。其次,表格的表征容量也是有限的,即使强化学习任务的状态和动作空间离散,如果状态-动作空间极大,则表格法也无能为力。
其实,表格只是值函数和策略函数的一种表征方式,适用于小规模离散情况,对于大规模或连续情况,可以用一个复杂函数模型来表征,例如用深度神经网络来表征值函数或策略函数,这正是深度强化学习的由来。
本章考虑状态空间连续、动作空间离散的强化学习任务。假设环境存在明确的初始状态和终止状态,并且可在有限步交互后达到终止状态,则称这种强化学习任务为有局的(Episodic)。从任何一个初始状态出发,经过有限次交互后到达终止状态的过程称为一局(Episode)。
1.线性值函数近似算法
状态空间连续的有局强化学习任务显然不能使用表格法求解。虽然也可以将连续状态空间离散化,但这容易造成“维数灾难”,并且离散化后精度也不能得到保证。在经典强化学习中,Q值矩阵的本质是一个将状态-动作对映射到实数域的离散函数,对于连续状态空间问题,可以用一个函数来近似这个映射关系,这个函数可以是线性函数、非线性函数、神经网络等。
1.1线性值函数近似时序差分算法
设环境的状态空间为S,动作空间为A,称映射:
ϕ
:
S
∗
A
→
R
l
\phi :S*A\to R^{l}
ϕ:S∗A→Rl
为状态-动作特征函数,它将环境的状态-动作对映射到一个抽象的特征空间。
假设状态空间是n维空间,即:
s
=
(
s
1
,
s
2
,
s
3
,
.
.
.
,
s
n
)
∈
R
n
s=(s_{1},s_{2},s_{3},...,s_{n})\in R^{n}
s=(s1,s2,s3,...,sn)∈Rn
动作空间是有限且离散的,一个比较简单的特征函数可以写成:
ϕ
(
s
,
a
i
)
≜
(
s
1
,
s
2
,
…
,
s
n
,
0
,
1
,
0
,
.
.
.
,
0
)
T
\phi (s,a_{i})\triangleq (s_{1},s_{2},\dots ,s_{n},0,1,0,...,0)^{T}
ϕ(s,ai)≜(s1,s2,…,sn,0,1,0,...,0)T
其中,
s
i
s_{i}
si表示第i种状态,(0,…,0,1,0,…,0)是指将
a
i
a_{i}
ai转化成One-Hot向量。
在策略
π
\pi
π下,将动作值函数近似为状态-动作特征向量的线性函数,系数向量为
θ
\theta
θ,即:
Q
^
π
(
s
,
a
;
θ
)
≜
ϕ
(
s
,
a
)
⋅
θ
\hat{Q}_{\pi} (s,a;\theta )\triangleq \phi (s,a)\cdot \theta
Q^π(s,a;θ)≜ϕ(s,a)⋅θ
强化化学习的目标是学习近似函数系数θ,使近似线性函数的值和实际动作值
Q
π
(
s
,
a
)
Q_π(s,a)
Qπ(s,a)尽量接近。可以使用最小二乘期望作为损失函数,即:
L
(
θ
)
≜
E
π
[
(
Q
π
(
s
,
a
)
−
Q
^
π
(
s
,
a
;
θ
)
2
]
L(\theta )\triangleq E_{\pi } [(Q_{\pi }(s,a)-\hat{Q}_{\pi} (s,a;\theta )^{2}]
L(θ)≜Eπ[(Qπ(s,a)−Q^π(s,a;θ)2]
其中,
E
π
E_{\pi}
Eπ表示根据策略
π
\pi
π采样而得到的平方误差的期望。
由此,强化学习的目标即可转换为:求解以
θ
\theta
θ为决策变量、以
L
(
θ
)
L(θ)
L(θ)为目标函数的无约束优化问题:
arg
min
θ
L
(
θ
)
≜
E
π
[
(
Q
π
(
s
,
a
)
−
Q
^
π
(
s
,
a
;
θ
)
2
]
θ
∈
R
l
\arg\min_{\theta }L(\theta )\triangleq E_{\pi } [(Q_{\pi }(s,a)-\hat{Q}_{\pi} (s,a;\theta )^{2}]\\ \theta\in R^{l}
argθminL(θ)≜Eπ[(Qπ(s,a)−Q^π(s,a;θ)2]θ∈Rl
采用梯度下降法最小化损失函数
L
(
θ
)
L(θ)
L(θ),损失函数关于
θ
\theta
θ的梯度为:
▽
θ
L
(
θ
)
=
[
∂
L
(
θ
)
θ
1
,
∂
L
(
θ
)
θ
2
,
⋯
,
∂
L
(
θ
)
θ
l
]
T
\triangledown _{\mathbf{\theta} } L(\mathbf{\theta } )= [\frac{\partial L(\mathbf{\theta } )}{\theta _{1}},\frac{\partial L(\mathbf{\theta } )}{\theta _{2}},\cdots ,\frac{\partial L(\mathbf{\theta } )}{\theta _{l}}]^{T}
▽θL(θ)=[θ1∂L(θ),θ2∂L(θ),⋯,θl∂L(θ)]T
其中
∂
L
(
θ
)
θ
i
=
−
E
π
[
2
(
Q
π
(
s
,
a
)
−
Q
^
π
(
s
,
a
;
θ
)
)
ϕ
(
s
,
a
)
]
\frac{\partial L(\mathbf{\theta } )}{\theta _{i}}=-E_{\pi } [2(Q_{\pi }(s,a)-\hat{Q}_{\pi} (s,a;\theta ))\phi (s,a)]
θi∂L(θ)=−Eπ[2(Qπ(s,a)−Q^π(s,a;θ))ϕ(s,a)]
则单个样本的更新规则:
θ
←
θ
+
α
(
Q
π
(
s
,
a
)
−
Q
^
π
(
s
,
a
;
θ
)
)
ϕ
(
s
,
a
)
\theta \leftarrow \theta +\alpha (Q_{\pi }(s,a)-\hat{Q}_{\pi} (s,a;\theta ))\phi (s,a)
θ←θ+α(Qπ(s,a)−Q^π(s,a;θ))ϕ(s,a)
上式不能真正用作算法迭代式,因为真实动作值
Q
π
(
s
,
a
)
Q_{\pi}(s,a)
Qπ(s,a)是未知的。可以借助时序差分强化学习的思想来解决这一问题,用TD目标值来近似真实动作值,即:
Q
π
(
s
,
a
)
≈
R
(
s
,
a
)
+
γ
Q
^
π
(
s
′
,
a
′
;
θ
)
Q_{\pi }(s,a)\approx R(s,a)+\gamma \hat{Q}_{\pi} (s^{'},a^{'};\theta )
Qπ(s,a)≈R(s,a)+γQ^π(s′,a′;θ)
于是得到线性值函数近似法的参数更新公式:
θ
←
θ
+
α
(
R
(
s
,
a
)
+
γ
ϕ
(
s
′
,
a
′
)
⋅
θ
−
ϕ
(
s
,
a
)
⋅
θ
)
ϕ
(
s
,
a
)
\theta \leftarrow \theta +\alpha (R(s,a)+\gamma \phi (s^{'},a^{'})\cdot \theta -\phi (s,a)\cdot \theta)\phi (s,a)
θ←θ+α(R(s,a)+γϕ(s′,a′)⋅θ−ϕ(s,a)⋅θ)ϕ(s,a)
1.2特征函数
线性值函数近似方法引起人们的兴趣不仅是因为它具有良好的收敛性质,也因为它在数据搜索和计算上的高效性,但线性值函数近似法的数值表现还取决于状态-动作特征函数。
状态-动作特征函数需要准确地描述状态-动作对的特征,它其实是为强化学习的训练过程提前准备了一些关于环境状态和动作的先验知识。一种比较简单的构造状态-动作特征向量的方式是直接将状态特征向量和动作特征向量拼接成状态-动作特征向量。
由于本章的讨论限于连续状态空间、离散动作空间的强化学习问题,离散动作一般直接使用One-Hot向量作为其特征向量,所以本节重点讨论连续状态空间的状态特征向量构造问题。如果是连续状态空间、连续动作空间强化学习问题,则只需将这些方法再应用到连续动作空间,得出连续动作的特征向量,然后将它们拼接成状态-动作特征向量。
常见线性值函数:多项式特征函数、傅里叶特征函数、粗编码、瓦片编码、径向基函数。
2.神经网络值函数近似法
对于比较复杂的动作值函数来讲,用线性函数近似显然是不够的。
用泛化能力更强的深度神经网络来近似动作值函数。
将线性函数换成深度神经网络会带来许多新的问题,例如神经网络的结构、损失函数、训练数据、训练方法等。
2.1DQN算法原理
2.1.1Q网络
将深度神经网络近似地动作值函数嵌入Q-learning算法框架就可得到Deep Q-learning算法,简称DQN。
DQN中用于近似动作值函数的深度神经网络简称Q网络。
根据强化学习任务的状态来选择,Q网络可以是任意一种神经网络:
(1)如果状态是由小规模向量来表示的,则可以选择一般前馈式深度神经网络。
(2)如果状态是图像信息,则可以选择卷积神经网络;如果状态是序列数据,则可以选择循环神经网络。
(3)如果状态是图像信息,则可以选择卷积神经网络;如果状态是序列数据,则可以选择循环神经网络。
无论选择什么网络,Q网络的输入输出结构是不变的,因此,可以将Q网络看作一个黑箱,只考虑其输入输出结构。
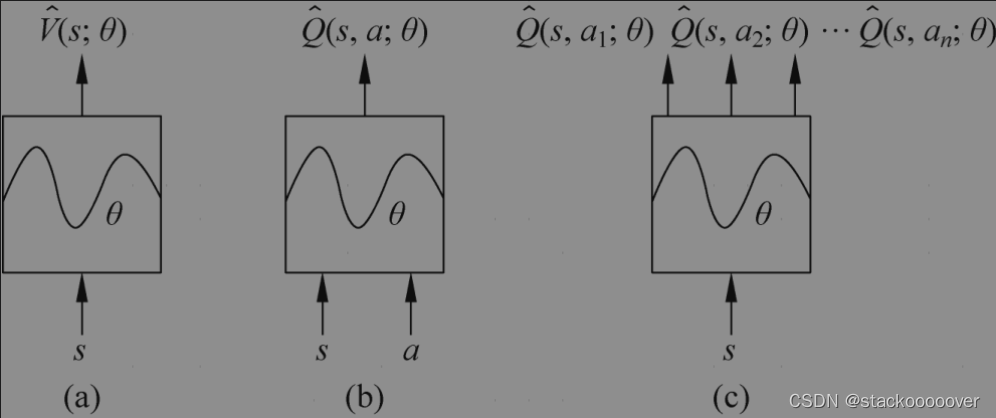
Q网络有以下3种输入输出结构:
(1)输入为状态s,输出为状态值
V
^
(
s
;
θ
)
\hat{V}(s;\theta )
V^(s;θ)。
(2)输入为状态-动作对(s,a),输出为动作值
Q
^
(
s
,
a
;
θ
)
\hat{Q}(s,a;\theta )
Q^(s,a;θ)。
(3)输入为状态s,输出为该状态下的所有动作值
Q
^
(
s
,
a
1
;
θ
)
,
Q
^
(
s
,
a
2
;
θ
)
,
⋯
,
Q
^
(
s
,
a
n
;
θ
)
\hat{Q}(s,a_{1} ;\theta ),\hat{Q}(s,a_{2} ;\theta ),\cdots ,\hat{Q}(s,a_{n} ;\theta )
Q^(s,a1;θ),Q^(s,a2;θ),⋯,Q^(s,an;θ)。
2.1.2损失函数
损失函数仍然是最小二乘的期望,即:
L
(
θ
)
≜
E
(
s
,
a
)
∼
π
[
(
Q
π
(
s
,
a
)
−
Q
^
π
(
s
,
a
;
θ
)
2
]
L(\theta )\triangleq E_{(s,a)\sim \pi } [(Q_{\pi }(s,a)-\hat{Q}_{\pi} (s,a;\theta )^{2}]
L(θ)≜E(s,a)∼π[(Qπ(s,a)−Q^π(s,a;θ)2]
由于不能直接计算,所以仍然使用TD目标值来近似真实动作值,即:
Q
π
(
s
,
a
)
≈
R
(
s
,
a
)
+
γ
Q
^
π
(
s
′
,
a
′
;
θ
)
Q_{\pi }(s,a)\approx R(s,a)+\gamma \hat{Q}_{\pi} (s^{'},a^{'};\theta )
Qπ(s,a)≈R(s,a)+γQ^π(s′,a′;θ)
2.1.3经验回放技术
经验回放技术是DQN的关键技术,可以说正是因为引入了经验回放技术,才能使深度学习和强化学习有机结合。
深度学习是监督学习,需要大量带标签的训练数据,但强化学习本身的机制并不能大量提供带标签的数据,这是将深度学习和强化学习结合的难点。
经验回放技术将历史经验数据存放在一个经验回放池中,这些经验数据通过计算整理,可以作为深度Q网络的训练数据使用,很好地解决了上述矛盾,达到了深度学习和强化学习的有机结合。
Q网络的输入是状态-动作对
(
s
,
a
)
(s,a)
(s,a),输出是预测动作值
Q
^
π
(
s
,
a
;
θ
)
\hat{Q}_{\pi} (s,a;\theta )
Q^π(s,a;θ),所以Q网络的训练数据也应该由状态-动作对和其对应的真实动作值组成,真实动作值使用TD目标值来近似真实动作值估计。
在DQN的训练过程中,智能体每次与环境交互都会产生一段MDP序列
(
s
,
a
,
R
,
s
′
,
e
n
d
)
(s,a,R,s′,end)
(s,a,R,s′,end)表示在状态
s
s
s下执行动作
a
a
a,环境状态转移到
s
′
s′
s′,并且反馈即时奖励
R
R
R和交互回合是否结束的指示end,令:
y
≜
{
R
,
i
f
e
n
d
=
T
r
u
e
R
+
γ
Q
^
π
(
s
′
,
a
′
;
θ
)
,
i
f
e
n
d
=
F
a
l
s
e
y\triangleq \left\{\begin{matrix} R,&if\space end=True\\ R+\gamma \hat{Q}_{\pi} (s^{'},a^{'};\theta ),&if \space end=False \end{matrix}\right.
y≜{R,R+γQ^π(s′,a′;θ),if end=Trueif end=False
则
y
y
y就是状态-动作对
(
s
,
a
)
(s,a)
(s,a)对应的真实动作值
Q
(
s
,
a
)
Q(s,a)
Q(s,a)的估计,称
y
y
y为TD目标值。这样,在当前时刻,之前交互生成的每段MDP序列
(
s
,
a
,
R
,
s
′
,
e
n
d
)
(s,a,R,s′,end)
(s,a,R,s′,end)都可以生成一个训练数据
(
(
s
,
a
)
,
y
)
((s,a),y)
((s,a),y),这些训练数据又可以用来训练当前Q网络。
经验回放技术就是指将历史上交互生成的MDP序列片段存储起来,然后在当前时刻转化成训练数据,并用这些训练数据来训练当前Q网络的过程。
在实际应用中,经验回放池是从无到有的,当在回放池中的训练数据还很少时(小于一个批量)是不能进行Q网络训练的,此时就要继续搜集经验数据,而暂时不开始训练Q网络,但随着交互的进行,回放池中的数据会一直增加。一般会设置一个回放池最大容量,当超出最大容量时,就将最初搜集的训练数据删除。删除最初的数据是因为随着训练的进行,越往后搜集到的经验数据质量越高。
2.1.4训练Q网络
训练Q网络实际上是求解优化问题:
arg
min
θ
L
(
θ
)
≜
E
π
[
(
Q
π
(
s
,
a
)
−
Q
^
π
(
s
,
a
;
θ
)
2
]
\arg\min_{\theta }L(\theta )\triangleq E_{\pi } [(Q_{\pi }(s,a)-\hat{Q}_{\pi} (s,a;\theta )^{2}]\
argθminL(θ)≜Eπ[(Qπ(s,a)−Q^π(s,a;θ)2]
在深度学习中,我们使用批量(Batch)数据来估计均值,再考虑到式TD目标值对
Q
(
s
,
a
)
Q(s,a)
Q(s,a)的近似估计,上述优化公式改写为:
arg
min
θ
L
θ
(
θ
)
≜
1
B
∑
i
=
1
B
(
y
i
−
Q
^
π
(
s
,
a
;
θ
)
)
2
\arg\min _{\theta }L_{\theta }(\theta )\triangleq \frac{1}{B} \sum_{i=1}^{B} (y_{i}-\hat{Q}_{\pi} (s,a;\theta))^{2}
argθminLθ(θ)≜B1i=1∑B(yi−Q^π(s,a;θ))2
其中,B为批量大小(Batch Size)。基于随机梯度下降的参数
θ
θ
θ更新公式为:
θ
←
θ
+
α
1
B
∑
i
=
1
B
(
y
i
−
Q
^
π
(
s
,
a
;
θ
)
)
▽
θ
Q
^
π
(
s
,
a
;
θ
)
\theta \leftarrow \theta +\alpha \frac{1}{B} \sum_{i=1}^{B} (y_{i}-\hat{Q}_{\pi} (s,a;\theta))\triangledown_{\theta} \hat{Q}_{\pi} (s,a;\theta)
θ←θ+αB1i=1∑B(yi−Q^π(s,a;θ))▽θQ^π(s,a;θ)
实际上,在Q网络训练时并不直接使用上述迭代式,而是通过神经网络的误差反向传播机制逐层更新权重参数和偏置参数。
2.2DQN算法流程
通常认为DQN算法有两个版本:DQN和DQN-2015。
DQN-2015主要对DQN的经验回放技术做了一些改进。
2.2.1DQN

2.2.2DQN-2015
在前一章节,TD目标值和预测动作值的计算使用了相同的Q网络,这相当于用由Q网络自身产生的数据来训练自己,导致预测值和目标值关联性太强,不利于算法的收敛和模型泛化能力的提高。
在Volodymyr Mnih等学者于2015年发表的论文中,他们对DQN算法的这一缺陷进行了优化,提出了双Q网络的构想。双Q网络的核心思想是使用两个结构相同但参数不同的Q网络来分别负责动作值预测和TD目标值计算任务。
负责动作值预测的Q网络叫作预测网络或当前网络,负责TD目标值计算的Q网络叫作目标网络。
预测网络和目标网络的网络结构相同,但参数更新频率和方式不同。预测网络在每个时间步都进行参数更新,更新方式是常规的Q网络训练,而目标网络每隔若干个时间步才进行参数更新,更新方式是直接复制预测网络的当前参数。
双Q网络的设计将动作值预测和TD目标值计算分离,使训练输出和预测输出的相关性大幅降低,有效地解决了训练过程的稳定性和收敛性问题。

3.DQN案例(CartPole-v0倒立钟摆)
import torch
from torch import nn
import numpy as np
import gym
import matplotlib.pyplot as plt
if torch.cuda.is_available():
device = 'cuda'
else:
device = 'cpu'
BATCH_SIZE = 32 # 批处理数据量
LR = 0.01 # 学习率
EPISILON = 0.9 # 贪婪阈值
GAMMA = 0.9 # 折扣系数
TARGET_REPLACE_ITER = 100 # 目标网络跟新频率
MEMORY_CAPACITY = 500 # 经验回放池大小
env = gym.make('CartPole-v1', render_mode='human')
STATE_SIZE = env.observation_space.shape[0] # 状态维度
ACTION_SIZE = env.action_space.n # 动作维度
# 定义Q网络
class QNet(nn.Module):
def __init__(self):
super(QNet, self).__init__()
self.flatten = nn.Flatten()
self.linear_ReLU_stack = nn.Sequential(
nn.Linear(STATE_SIZE, 20),
nn.ReLU(),
nn.Linear(20, 20),
nn.ReLU(),
nn.Linear(20, ACTION_SIZE)
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_ReLU_stack(x)
return logits
# 定义DQN2015
class DQN2015(object):
def __init__(self):
self.eval_net, self.target_net = QNet().to(device), QNet().to(device) # 评价网络和目标网络
self.learn_step_counter = 0 # 学习步数记录
self.memory_counter = 0 # 回放池存储量
# 存储空间容量:(s,a,r,s_next),a,r为标量,s,s_next是维度STATE_SIZE的向量
self.memory = np.zeros((MEMORY_CAPACITY, STATE_SIZE * 2 + 2))
self.optimazer = torch.optim.Adam(self.eval_net.parameters(), lr=LR) # 优化器
self.loss_func = nn.MSELoss().to(device) # 均方误差损失函数
def choose_action(self, x): # 动作选择策略
x = torch.unsqueeze(torch.FloatTensor(x), 0).to(device)
action_value = self.eval_net(x) # 神经网络模拟的动作值
# e-greedy动作选择:小于阈值,贪婪;大于阈值,随机
if np.random.uniform() < EPISILON:
action_value = self.eval_net(x) # 神经网络模拟的动作值
action = torch.max(action_value, 1)[1].data.cpu().numpy()
action = action[0]
else:
action = np.random.randint(0, ACTION_SIZE)
return action
def store_transition(self, s, a, r, s_next):
transition = np.hstack((s, a, r, s_next))
# 如果没有满,把数据插入index后,如果满了,覆盖之前的旧数据
index = self.memory_counter % MEMORY_CAPACITY # 新数据在
self.memory[index, :] = transition
self.memory_counter += 1
def learn(self):
# 如果到达目标网络更新轮数,将评价网络的参数给目标网络
if self.learn_step_counter % TARGET_REPLACE_ITER == 0:
self.target_net.load_state_dict(self.eval_net.state_dict())
self.learn_step_counter += 1
# 在[0,MEMORY_CAPACITY)内随机抽取BATCH_SIZE个数,可能会重复
sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE)
b_memory = self.memory[sample_index, :]
# 以BATCH_SIZE为一组,分别取出s,a,r,s_next的值
b_s = torch.FloatTensor(b_memory[:, :STATE_SIZE]).to(device)
b_a = torch.LongTensor(b_memory[:, STATE_SIZE:STATE_SIZE + 1]).to(device)
b_r = torch.FloatTensor(b_memory[:, STATE_SIZE + 1:STATE_SIZE + 2]).to(device)
b_s_next = torch.FloatTensor(b_memory[:, -STATE_SIZE:]).to(device)
q_eval = self.eval_net(b_s).gather(1, b_a) # 将b_a中动作编号作为索引,取出对应动作的Q值(动作预测值)
q_next = self.target_net(b_s_next).detach() # 取出目标网络对应的next动作q值
q_target = b_r + GAMMA * q_next.max(1)[0].view(BATCH_SIZE, 1) # TD目标值
loss = self.loss_func(q_eval, q_target)
self.optimazer.zero_grad()
loss.backward()
self.optimazer.step()
if __name__ == '__main__':
dqn = DQN2015()
reward_list = []
for i in range(500):
s, _ = env.reset()
episode_reward_sum = 0
print(f'*********************************第{i}轮****************************')
while True:
env.render()
a = dqn.choose_action(s)
s_next,r,done,info,_ = env.step(a)
# 可以修改reward值让其训练速度加快
x, x_dot, theta, theta_dot = s_next
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
new_r = r1 + r2
dqn.store_transition(s,a,new_r,s_next)
episode_reward_sum+=r
s = s_next
if dqn.memory_counter>MEMORY_CAPACITY:
dqn.learn()
if done:
print(f'episode:{i},reward_sum:{episode_reward_sum}')
reward_list.append(episode_reward_sum)
break
x_list = [x for x in range(0,500)]
plt.title('Episode Reward')
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.plot(x_list,reward_list)
plt.show()
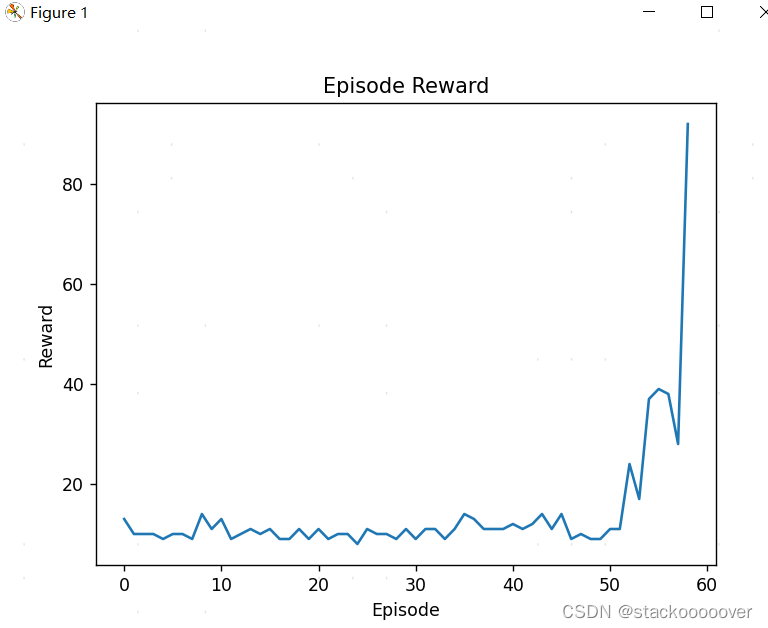
智能体可视化

reward曲线(可以看到,在第50轮的时候,已经开始收敛)