粒子群优化算法求解TSP旅行商问题C++(2020.11.12)_jing_zhong的博客-CSDN博客
混合粒子群算法(PSO):C++实现TSP问题 - 知乎 (zhihu.com)
一、原理
又是一个猜答案的算法,和遗传算法比较像,也是设置迭代次数,控制什么时候结束,然后设置粒子种群,每个种群代表一个访问城市的路径,代价函数就是访问一遍的路径和。
初始的时候,随机初始化30个粒子群(可自己设置),然后从这30个例子群里,找一个种群代价最优的结果,存入gbest路径。接着就是每次迭代更新粒子种群,更新思路是每个粒子包含一条访问城市的路径,对每个粒子中的点产生一个速度(这个速度有一共对应公式,v = w * v_cur + c1 * r1 * (x_best - x_cur) +c2 * r2(x_gbest - x_cur)),通过这个速度更新访问城市的路径(x = x + v),当然这个速度作用于城市序号上,会产生小数和重叠,以及不能让这个速度太大,需要限定在一定范围内,如果出现城市序号重复,则需要将重复的序号换成没有出现的序号。
最后每迭代一次,计算一次全局最优粒子,直到迭代结束。
如果访问29个城市,暴力枚举需要计算28!= 304 888 344 611 713 860 501 504 000 000 。可见随着城市数量的增加,计算量是指数级上升,如果使用粒子群算法,计算量30*500=15000,计算量是线性的,确实很有优势。
二、代码
1 1150.0 1760.0
2 630.0 1660.0
3 40.0 2090.0
4 750.0 1100.0
5 750.0 2030.0
6 1030.0 2070.0
7 1650.0 650.0
8 1490.0 1630.0
9 790.0 2260.0
10 710.0 1310.0
11 840.0 550.0
12 1170.0 2300.0
13 970.0 1340.0
14 510.0 700.0
15 750.0 900.0
16 1280.0 1200.0
17 230.0 590.0
18 460.0 860.0
19 1040.0 950.0
20 590.0 1390.0
21 830.0 1770.0
22 490.0 500.0
23 1840.0 1240.0
24 1260.0 1500.0
25 1280.0 790.0
26 490.0 2130.0
27 1460.0 1420.0
28 1260.0 1910.0
29 360.0 1980.0
#include <iostream>
#include <string>
#include <fstream>
#include <time.h>
#include <random>
using namespace std;
const int citycount = 29;
double vmax = 1, vmin = -1;
std::default_random_engine random(time(NULL));//通过time这个随机数种子,每次产生不同的随机数
static std::uniform_real_distribution<double> distribution(0.0, std::nextafter(1.0, DBL_MAX));// C++11提供的实数均匀分布模板类 0~1
static std::uniform_real_distribution<double> distribution1(vmin, std::nextafter(vmax, DBL_MAX));//-1~1
class City
{
public:
string name;//城市名称
double x, y;//城市点的二维坐标
void shuchu()
{
std::cout << name + ":" << "(" << x << "," << y << ")" << endl;
}
};
class Graph
{
public:
City city[citycount];//城市数组
double distance[citycount][citycount];//城市间的距离矩阵
void Readcoordinatetxt(string txtfilename)//读取城市坐标文件的函数
{
ifstream myfile(txtfilename, ios::in);
double x = 0, y = 0;
int z = 0;
if (!myfile.fail())
{
int i = 0;
while (!myfile.eof() && (myfile >> z >> x >> y))
{
city[i].name = to_string(z);//城市名称转化为字符串
city[i].x = x; city[i].y = y;
i++;
}
}
else
cout << "文件不存在";
myfile.close();
//计算城市距离矩阵
for (int i = 0; i < citycount; i++)//29
for (int j = 0; j < citycount; j++)
{
distance[i][j] = sqrt((pow((city[i].x - city[j].x), 2) + pow((city[i].y - city[j].y), 2)) / 10.0);//计算城市ij之间的伪欧式距离
if (round(distance[i][j] < distance[i][j])) distance[i][j] = round(distance[i][j]) + 1;
else distance[i][j] = round(distance[i][j]);//round向上取整
}
}
void shuchu()
{
cout << "城市名称 " << "坐标x" << " " << "坐标y" << endl;
for (int i = 0; i < citycount; i++)
city[i].shuchu();
cout << "距离矩阵: " << endl;
for (int i = 0; i < citycount; i++)
{
for (int j = 0; j < citycount; j++)
{
if (j == citycount - 1)
std::cout << distance[i][j] << endl;
else
std::cout << distance[i][j] << " ";
}
}
}
};
Graph Map_City;//定义全局对象图,放在Graph类后
int * Random_N(int n)
{
int *geti;
geti = new int[n];
int j = 0;
while (j < n)
{
while (true)
{
int flag = -1;
int temp = rand() % n + 1;//随机取1~29
if (j > 0)
{
int k = 0;
for (; k < j; k++)
{
if (temp == *(geti + k))break;
}
if (k == j)
{
*(geti + j) = temp;
flag = 1;
}
}
else
{
*(geti + j) = temp;
flag = 1;
}
if (flag == 1)break;
}
j++;
}
return geti;
}
double Evaluate(int *x)//计算粒子适应值的函数
{
double fitnessvalue = 0;
for (int i = 0; i < citycount - 1; i++)
fitnessvalue += Map_City.distance[x[i] - 1][x[i + 1] - 1];
fitnessvalue += Map_City.distance[x[citycount - 1] - 1][x[0] - 1];//城市尾与第一个城市的距离,x是一组路线的序号
return fitnessvalue;
}
class Particle
{
public:
int *x;//粒子的位置 一条路径
int *v;//粒子的速度
double fitness;
void Init()
{
x = new int[citycount];
v = new int[citycount];
int *M = Random_N(citycount);//随机生成一组路径
for (int i = 0; i < citycount; i++)
x[i] = *(M + i);
fitness = Evaluate(x);//计算这组路径的代价
for (int i = 0; i < citycount; i++)
{
v[i] = (int)distribution1(random);//产生-1~1之间的随机数
}
}
void shuchu()
{
for (int i = 0; i < citycount; i++)
{
if (i == citycount - 1)
std::cout << x[i] << ") = " << fitness << endl;
else if (i == 0)
std::cout << "f(" << x[i] << ",";
else
std::cout << x[i] << ",";
}
}
};
void Adjuxt_validParticle(Particle p)//调整粒子有效性的函数,使得粒子的位置符合TSP问题解的一个排列
{
int route[citycount];//1-citycount
bool flag[citycount];//对应route数组中是否在粒子的位置中存在的数组,参考数组为route
int biaoji[citycount];//对粒子每个元素进行标记的数组,参考数组为粒子位置x
for (int j = 0; j < citycount; j++)
{
route[j] = j + 1;
flag[j] = false;
biaoji[j] = 0;
}
//首先判断粒子p的位置中是否有某个城市且唯一,若有且唯一,则对应flag的值为true,
for (int j = 0; j < citycount; j++)
{
int num = 0;
for (int k = 0; k < citycount; k++)
{
if (p.x[k] == route[j])
{
biaoji[k] = 1;//说明粒子中的k号元素对应的城市在route中,并且是第一次出现才进行标记
num++; break;
}
}
if (num == 0) flag[j] = false;//粒子路线中没有route[j]这个城市
else if (num == 1) flag[j] = true;//粒子路线中有route[j]这个城市
}
for (int k = 0; k < citycount; k++)
{
if (flag[k] == false)//粒子路线中没有route[k]这个城市,需要将这个城市加入到粒子路线中
{
int i = 0;
for (; i < citycount; i++)
{
if (biaoji[i] != 1)break;
}
p.x[i] = route[k];//对于标记为0的进行替换
biaoji[i] = 1;
}
}
}
class PSO
{
public:
Particle *oldparticle; //当前粒子种群信息
Particle *pbest; //每个个体最优
Particle gbest;//群体最优
double c1, c2, w;
int Itetime;
int popsize;
void Init(int Pop_Size, int itetime, double C1, double C2, double W)
{
Itetime = itetime;//迭代500次
c1 = C1;//2
c2 = C2;//2
w = W;//0.8
popsize = Pop_Size;//30
oldparticle = new Particle[popsize];//30个粒子,每个粒子包含一条随机路径
pbest = new Particle[popsize];//30个粒子
for (int i = 0; i < popsize; i++)//初始化30次
{
oldparticle[i].Init();//初始化30个粒子群
pbest[i].Init();//初始化30个粒子群
for (int j = 0; j < citycount; j++)
{
pbest[i].x[j] = oldparticle[i].x[j];
pbest[i].fitness = oldparticle[i].fitness;
}
}
gbest.Init(); //初始化一个粒子群
gbest.fitness = INFINITY;//初始设为极大值
for (int i = 0; i < popsize; i++)//遍历30个粒子群
{
if (pbest[i].fitness < gbest.fitness)//如果当前粒子群代价比种群最小的代价还小,则更新其
{
gbest.fitness = pbest[i].fitness;
for (int j = 0; j < citycount; j++)//29个城市点
gbest.x[j] = pbest[i].x[j];//最优路径的路径
}
}
}
void Shuchu()
{
for (int i = 0; i < popsize; i++)
{
std::cout << "粒子" << i + 1 << "->";
oldparticle[i].shuchu();
}
std::cout << "当前最优粒子:" << std::endl;
gbest.shuchu();
}
void PSO_TSP(int Pop_size, int itetime, double C1, double C2, double W, double Vlimitabs, string filename)
{
Map_City.Readcoordinatetxt(filename);//计算城市间距离矩阵
Map_City.shuchu();//输出初始城市位置和距离矩阵
vmax = Vlimitabs; //3
vmin = -Vlimitabs;//-3
Init(Pop_size, itetime, C1, C2, W);//在随机初始的粒子群中,找到一个最优的粒子
std::cout << "初始化后的种群如下:" << endl;
Shuchu();//输出初始种群及最优路径
//向文件中写入城市坐标,距离矩阵
ofstream outfile;
outfile.open("result.txt", ios::trunc);
outfile << "城市名称 " << "坐标x" << " " << "坐标y" << endl;
for (int i = 0; i < citycount; i++)
outfile << Map_City.city[i].name << " " << Map_City.city[i].x << " " << Map_City.city[i].y << endl;
outfile << "距离矩阵: " << endl;
for (int i = 0; i < citycount; i++)
{
for (int j = 0; j < citycount; j++)
{
if (j == citycount - 1)
outfile << Map_City.distance[i][j] << endl;
else
outfile << Map_City.distance[i][j] << " ";
}
}
outfile << "初始化后的种群如下:" << endl;
for (int i = 0; i < popsize; i++)
{
outfile << "粒子" << i + 1 << "->";
for (int j = 0; j < citycount; j++)//29
{
if (j == citycount - 1)
outfile << oldparticle[i].x[j] << ") = " << oldparticle[i].fitness << endl;
else if (j == 0)
outfile << "f(" << oldparticle[i].x[j] << ",";
else
outfile << oldparticle[i].x[j] << ",";
}
}
for (int ite = 0; ite < Itetime; ite++)//500次
{
for (int i = 0; i < popsize; i++)//30
{
//更新粒子速度和位置
for (int j = 0; j < citycount; j++)//29
{
//v= w*v_oldP + c1*r1*(x_bestP - x_oldP) +c2*r2(x_gbest - x_oldP)
oldparticle[i].v[j] = (int)(w*oldparticle[i].v[j] + c1 * distribution(random)*(pbest[i].x[j] - oldparticle[i].x[j]) + c2 * distribution(random)*(gbest.x[j] - oldparticle[i].x[j]));
if (oldparticle[i].v[j] > vmax)//粒子速度越界调整
oldparticle[i].v[j] = (int)vmax;
else if (oldparticle[i].v[j] < vmin)
oldparticle[i].v[j] = (int)vmin;
oldparticle[i].x[j] += oldparticle[i].v[j];//x=x+v
if (oldparticle[i].x[j] > citycount)oldparticle[i].x[j] = citycount;//粒子位置越界调整 让路径的每个点像速度一样变化取整
else if (oldparticle[i].x[j] < 1) oldparticle[i].x[j] = 1;
}
//粒子位置有效性调整,必须满足解空间的条件
Adjuxt_validParticle(oldparticle[i]);//对重复的城市去重
oldparticle[i].fitness = Evaluate(oldparticle[i].x);//计算当前粒子的代价
pbest[i].fitness = Evaluate(pbest[i].x);
if (oldparticle[i].fitness < pbest[i].fitness)//如果当前粒子的代价比之前历史中粒子的代价都小,则替换为历史最小代价
{
for (int j = 0; j < citycount; j++)
pbest[i].x[j] = oldparticle[i].x[j];
}//更新单个粒子的历史极值
for (int j = 0; j < citycount; j++)
gbest.x[j] = pbest[i].x[j];//更新全局极值
for (int k = 0; k < popsize && k != i; k++)//30 从单个最优中找一个全局最优保存起来
{
if (Evaluate(pbest[k].x) < Evaluate(gbest.x))
{
for (int j = 0; j < citycount; j++)
gbest.x[j] = pbest[k].x[j];
gbest.fitness = Evaluate(gbest.x);
}
}
}//迭代30次
outfile << "第" << ite + 1 << "次迭代后的种群如下:" << endl;
for (int i = 0; i < popsize; i++)
{
outfile << "粒子" << i + 1 << "->";
for (int j = 0; j < citycount; j++)
{
if (j == citycount - 1)
outfile << oldparticle[i].x[j] << ") = " << oldparticle[i].fitness << endl;
else if (j == 0)
outfile << "f(" << oldparticle[i].x[j] << ",";
else
outfile << oldparticle[i].x[j] << ",";
}
}
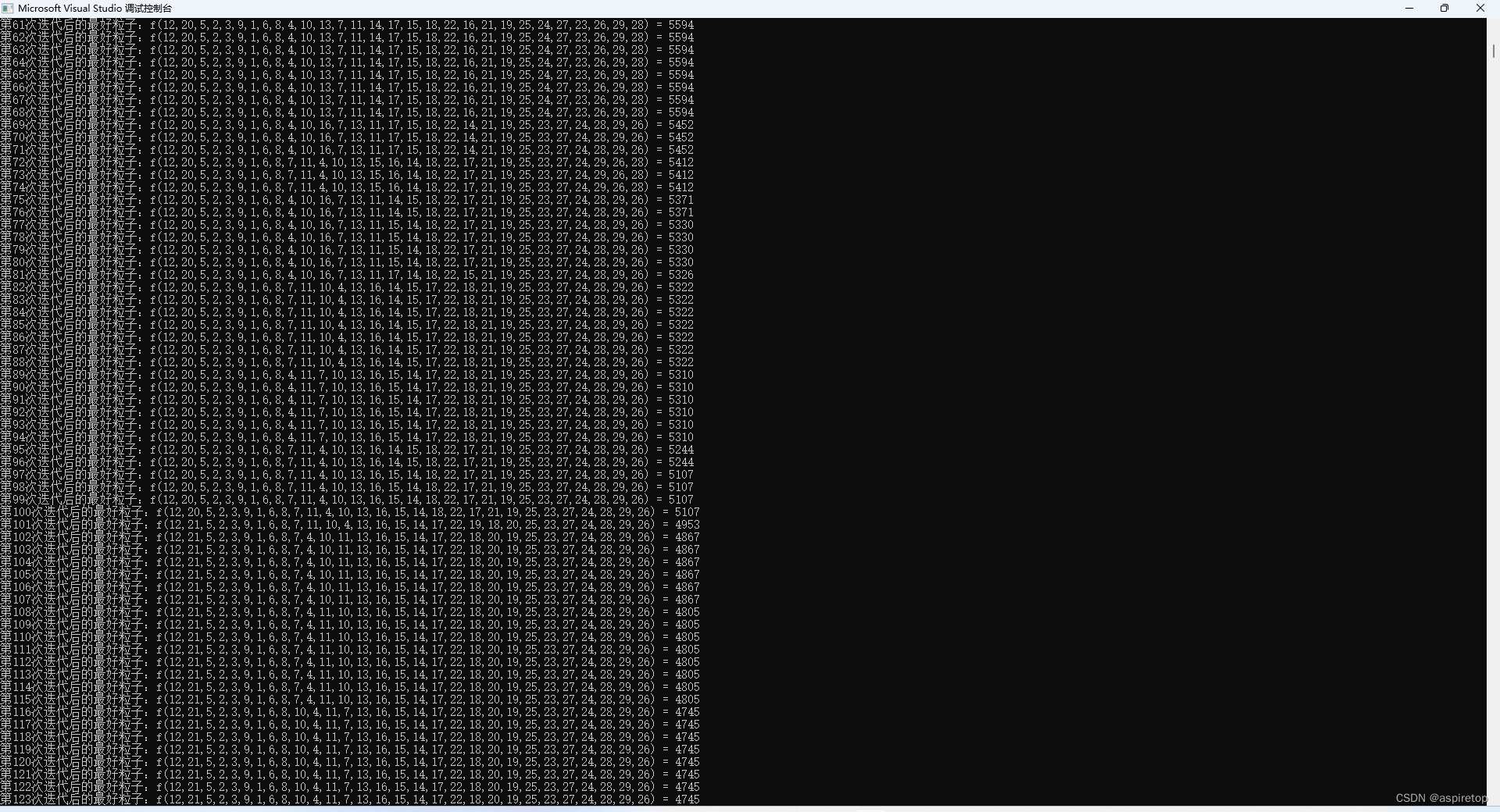
std::cout << "第" << ite + 1 << "次迭代后的最好粒子:";
outfile << "第" << ite + 1 << "次迭代后的最好粒子:" << endl;
for (int j = 0; j < citycount; j++)
{
if (j == citycount - 1)
outfile << gbest.x[j] << ") = " << gbest.fitness << endl;
else if (j == 0)
outfile << "f(" << gbest.x[j] << ",";
else
outfile << gbest.x[j] << ",";
}
gbest.shuchu();//每次迭代的全局最优
}
outfile.close();
}
};
int main()
{
PSO pso;
std::cout << "粒子群优化算法求解TSP旅行商问题" << endl;
pso.PSO_TSP(30, 500, 2, 2, 0.8, 3.0, "data.txt");
system("pause");
return 0;
}