目录
1. 三维物体的表面表达方式
1.1 边界表示法 (Boundary Representation)
1.2 空间划分法 (Spatial-Partitioning Representations)
1.3 构造体素法 (Boundary Constructive Solid Geometry)
2. 三维模型的表述方式
3. 基于符号距离场的表面重建方法
3.1 符号距离函数(Signed Distance Function)
3.2 基于隐函数的表面重建
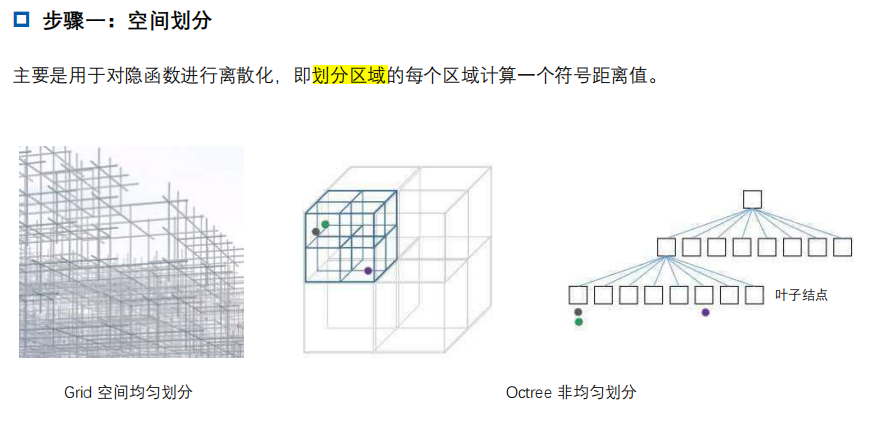
步骤一:空间划分
步骤二:符号距离场构建
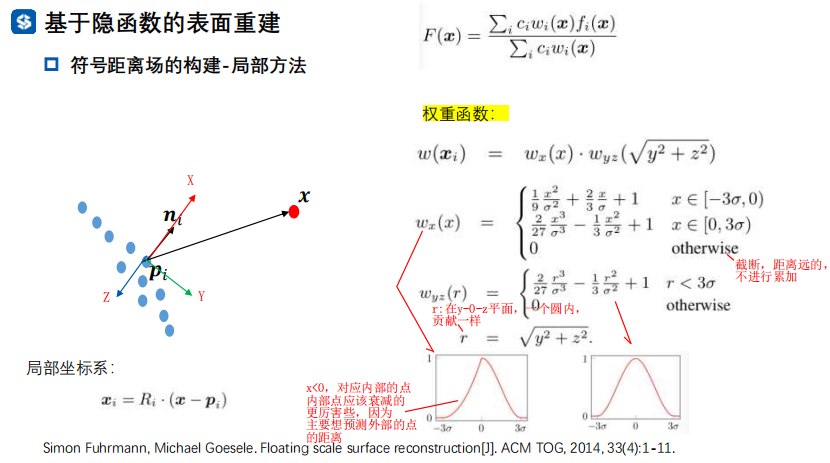
FSSR方法的符号距离函数定义
符号距离场的构建-全局方法
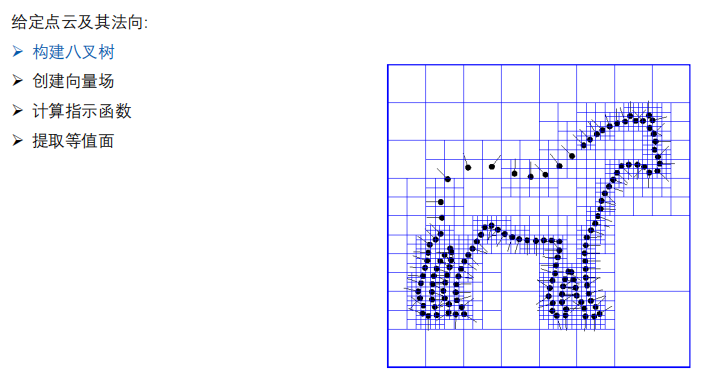
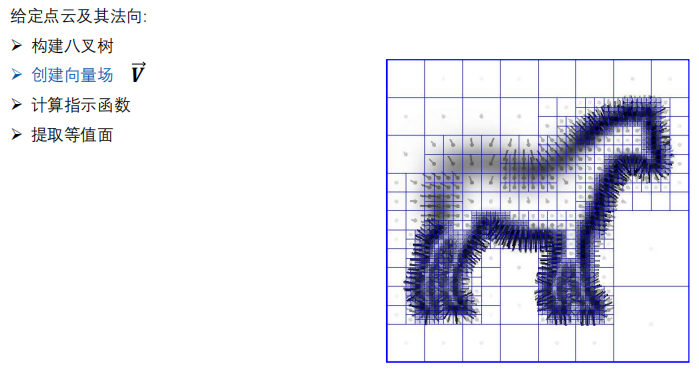
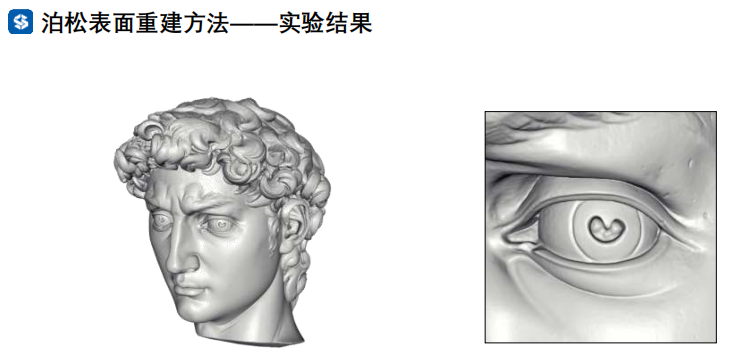
泊松表面重建方法
步骤三: Marching Cube生成表面(二维)
3.3 基于二元分割的表面重建方法
德劳内三角剖分 Delaunay Triangulation
二分类
总结
参考
1. 三维物体的表面表达方式
✓
边界表示法
✓
空间划分法
✓
构造体素法
1.1 边界表示法 (Boundary Representation)
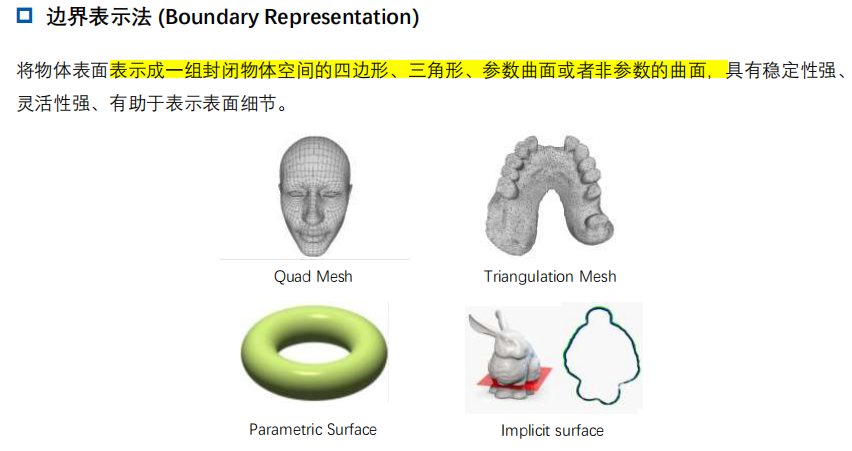
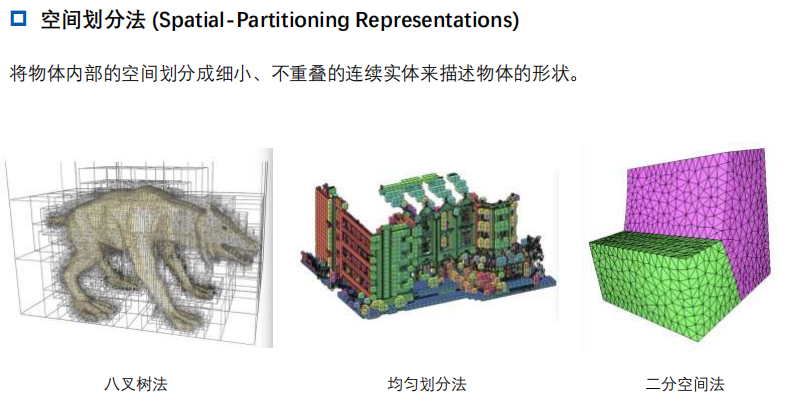
1.2 空间划分法 (Spatial-Partitioning Representations)
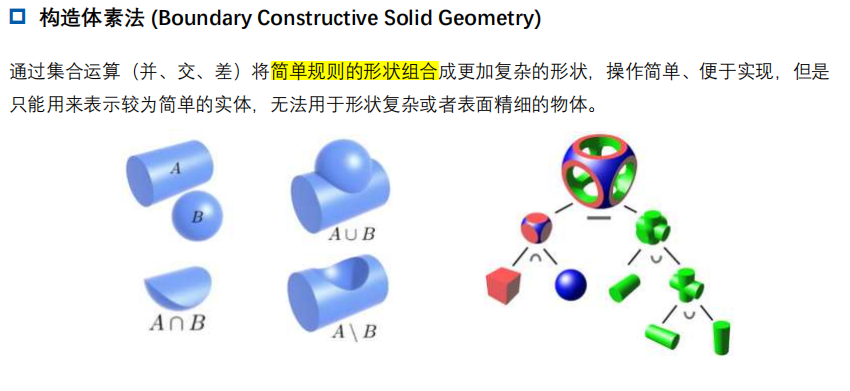
1.3 构造体素法 (Boundary Constructive Solid Geometry)
2. 三维模型的表述方式

3. 基于符号距离场的表面重建方法
✓
基本概念
✓
重建流程
✓
符号距离场的计算方法
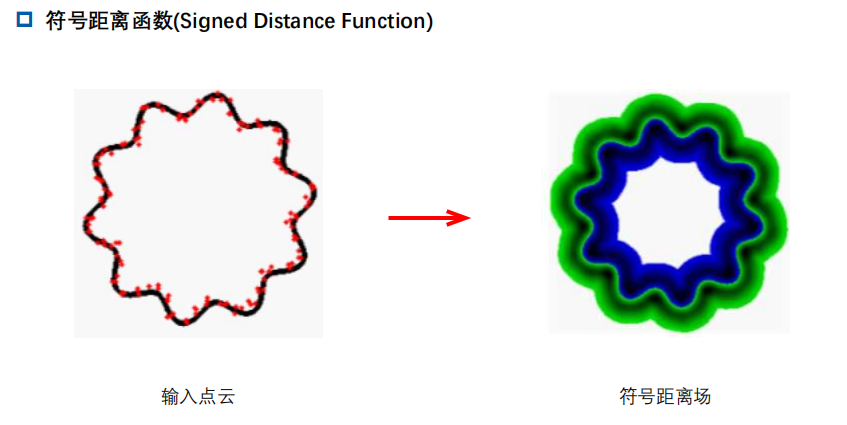
3.1 符号距离函数(Signed Distance Function)

3.2 基于隐函数的表面重建
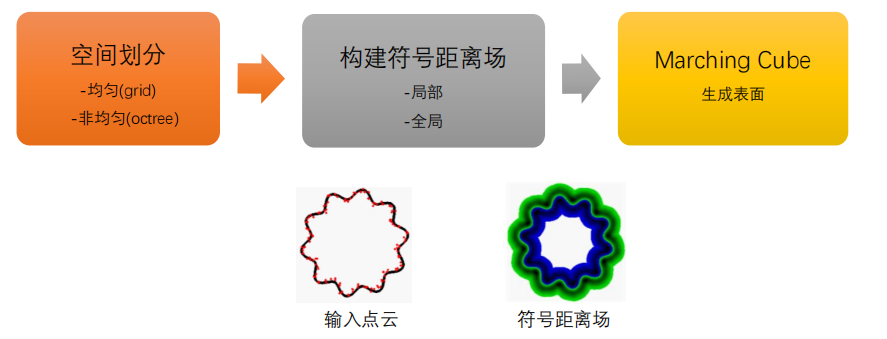
步骤一:空间划分
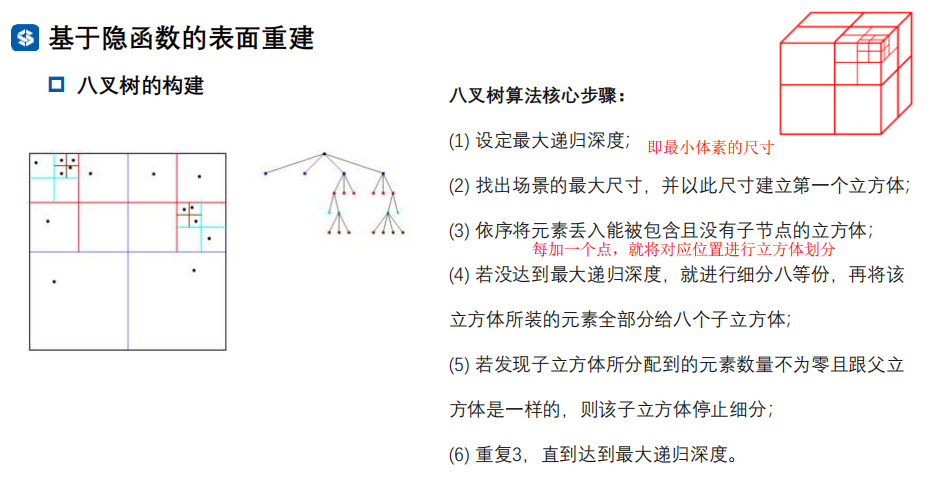
步骤二:符号距离场构建

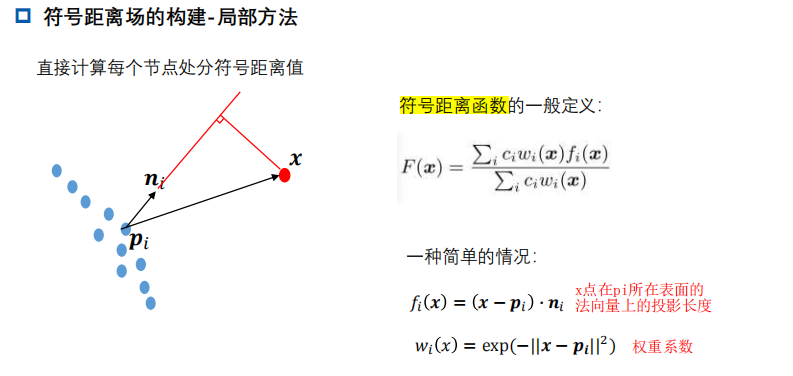
FSSR方法的符号距离函数定义

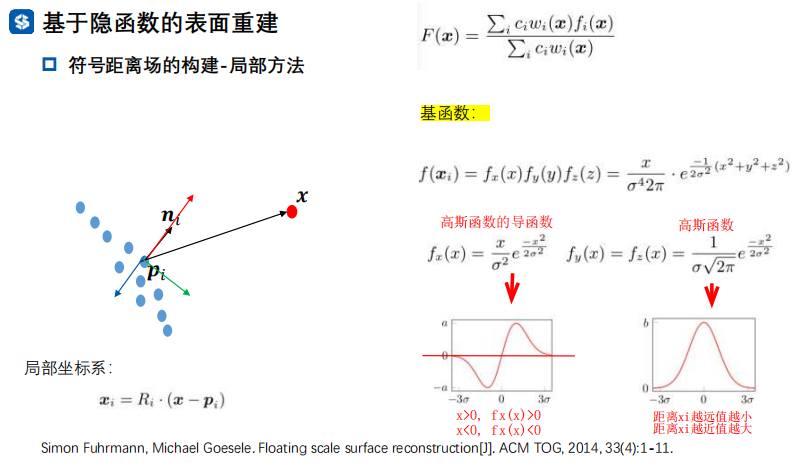
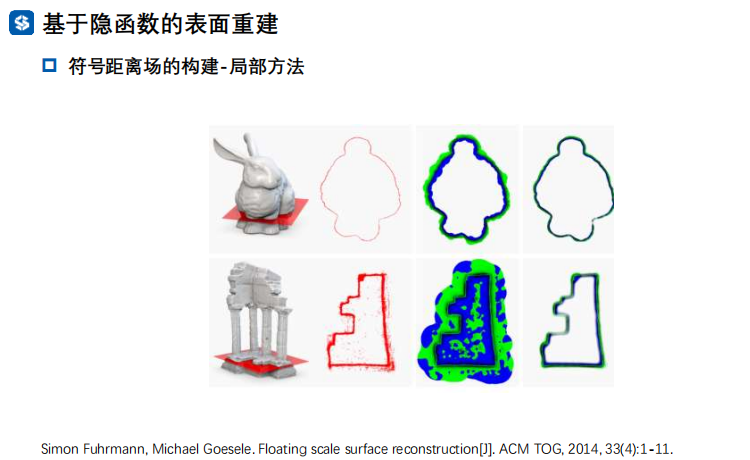
符号距离场的构建-全局方法
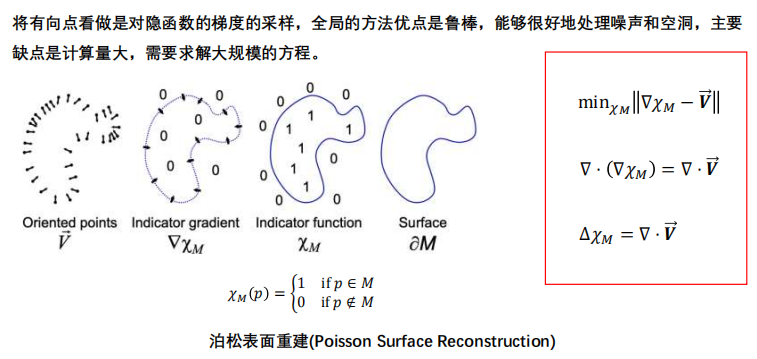
泊松表面重建方法



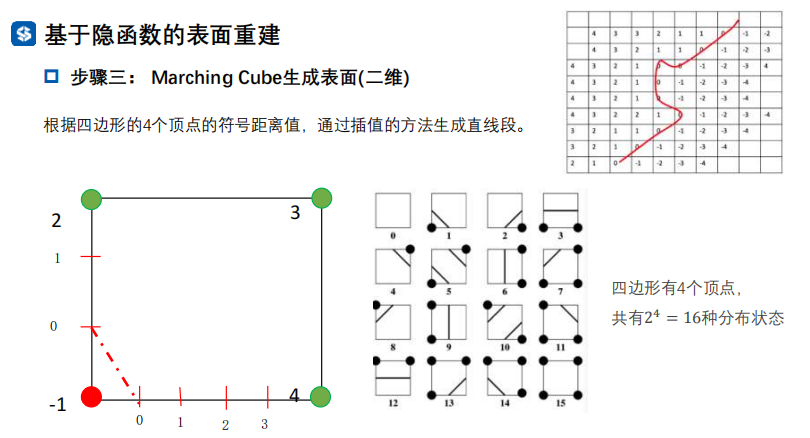
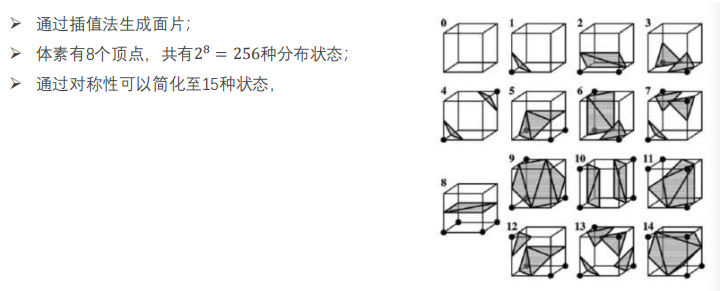
步骤三: Marching Cube生成表面(二维)
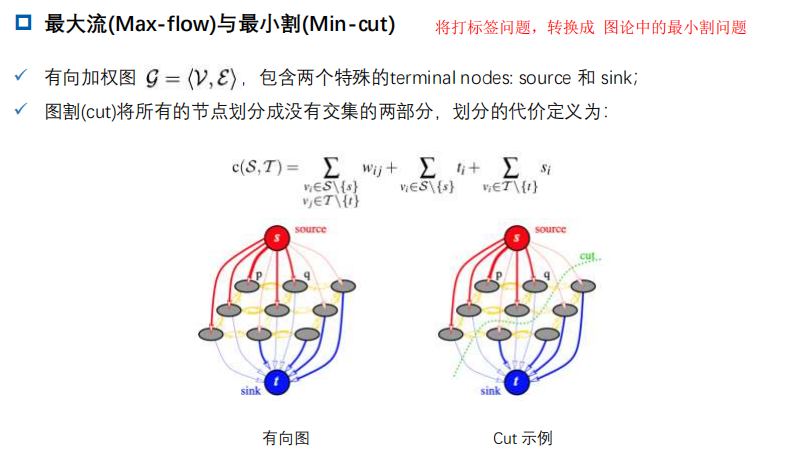
3.3 基于二元分割的表面重建方法
主要思想: 将空间划分成一组cell(voxel/tetrahedron),采用二元分割的思想,将这些cell划分成内部和外部两类, 介于interior和exterior面,即为物体的surface。
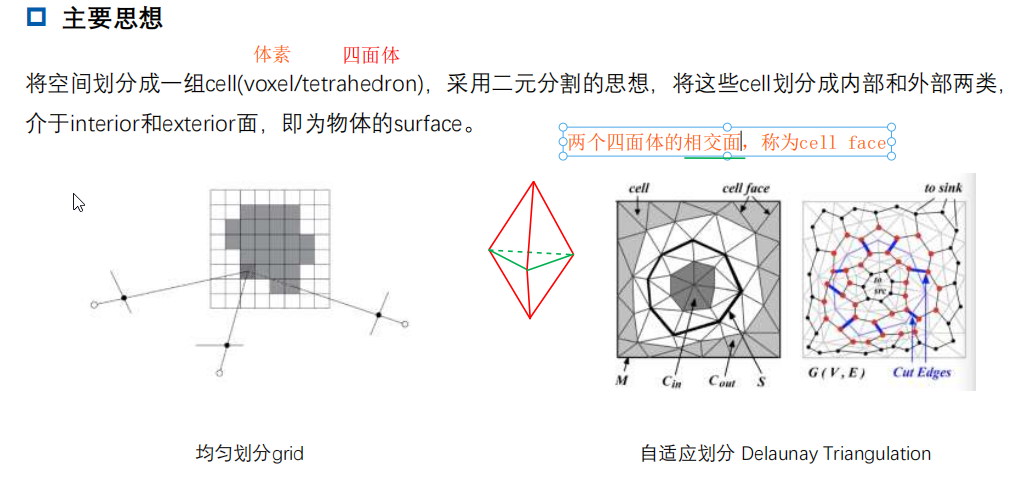
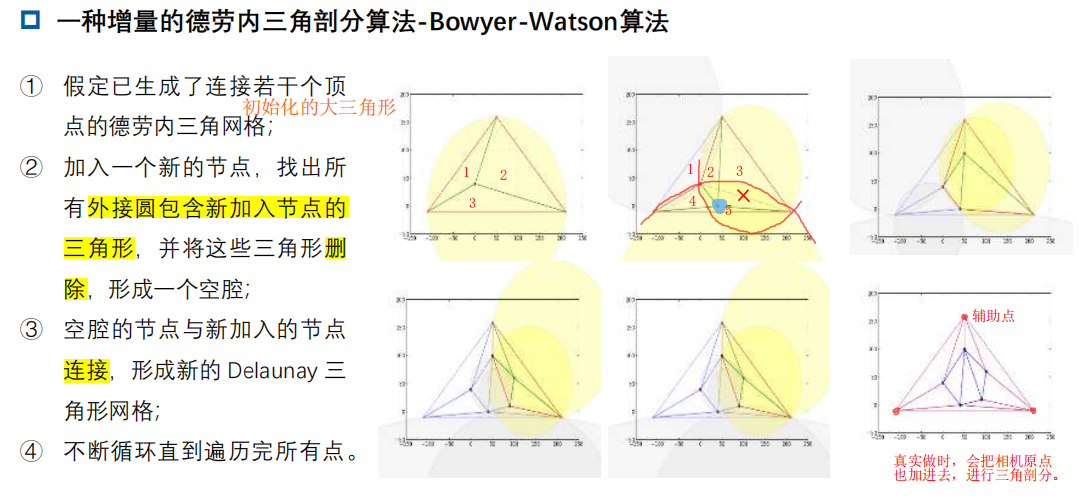
德劳内三角剖分 Delaunay Triangulation
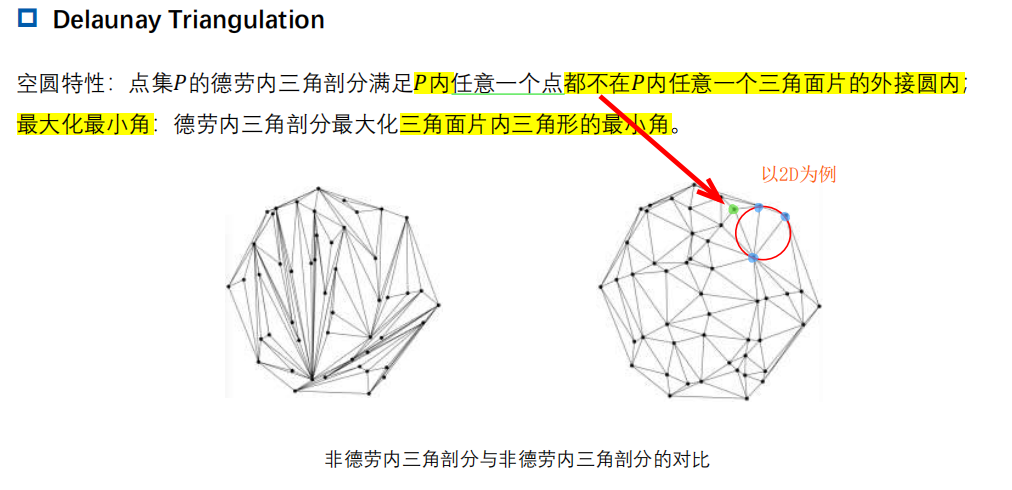
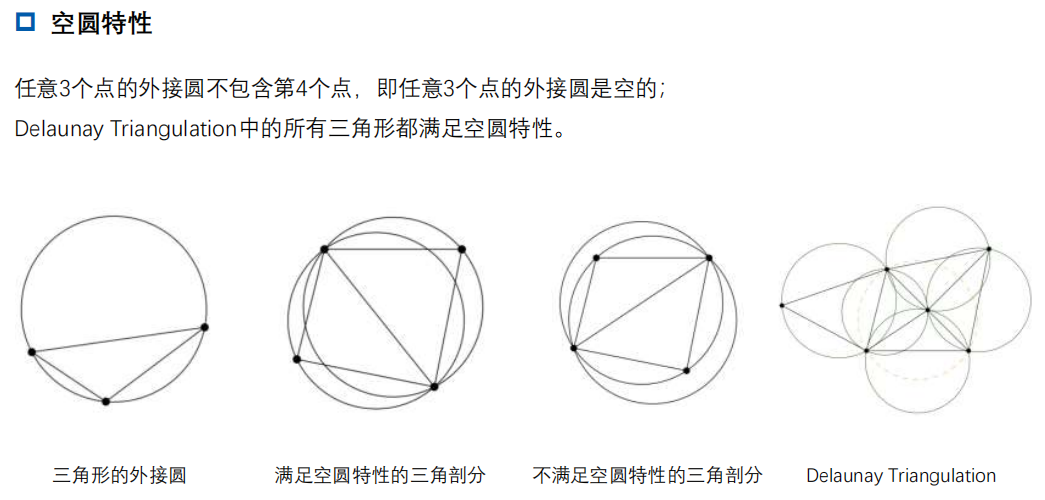
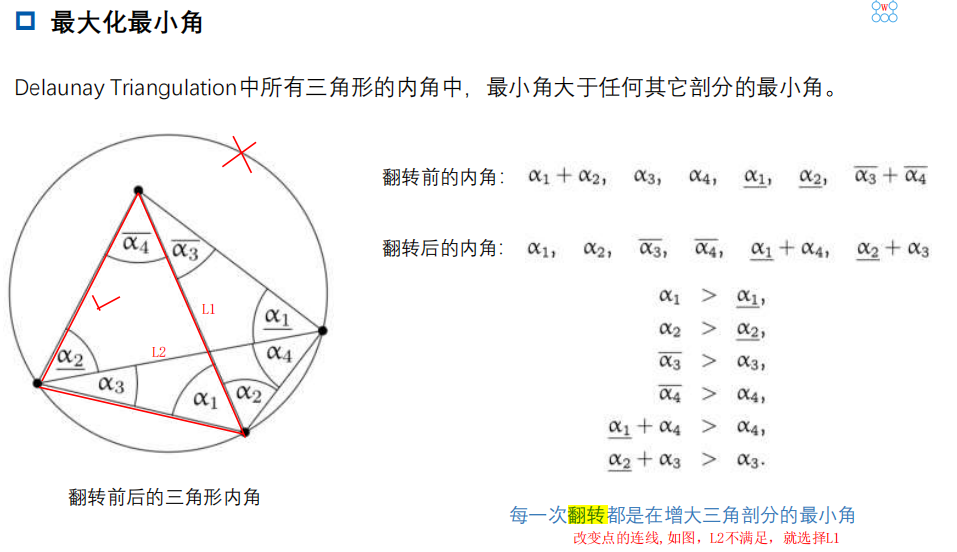
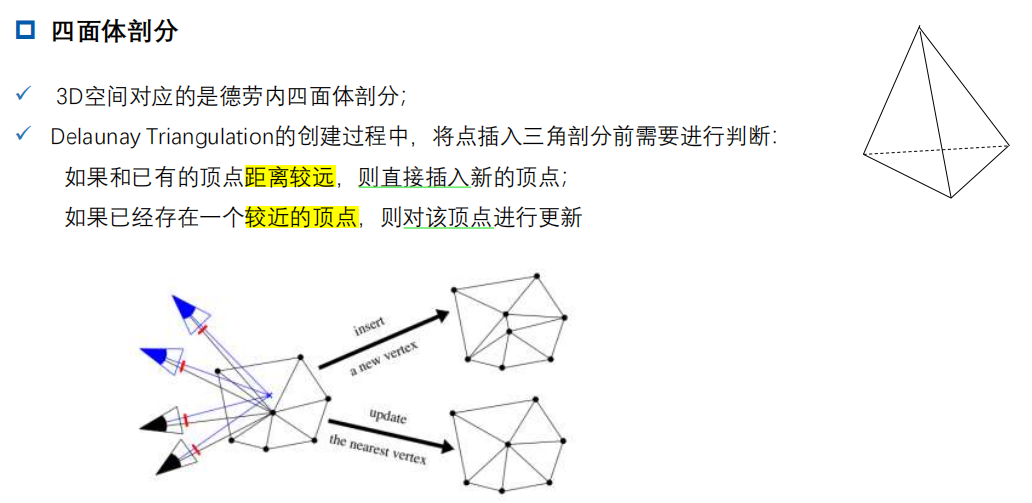
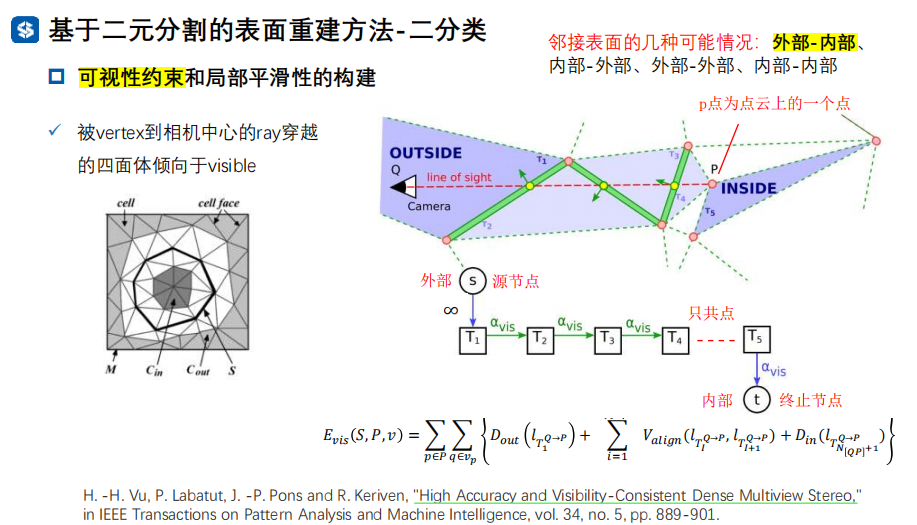
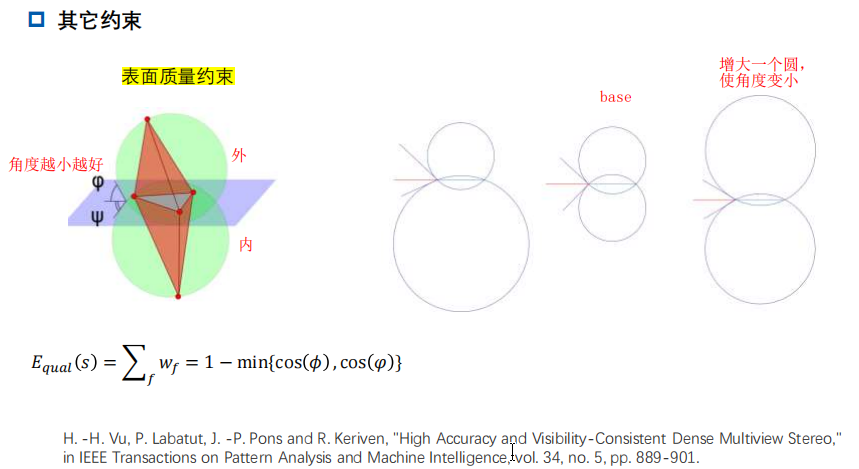
二分类

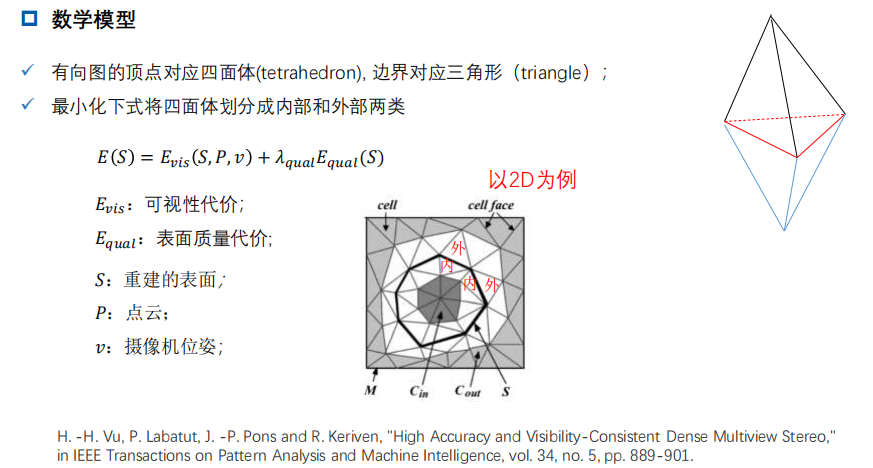
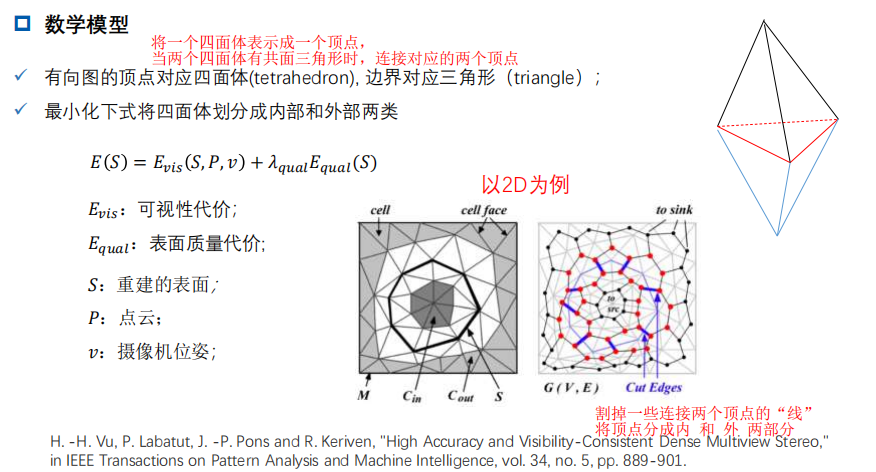


总结
- ✓ 算法流程简单,容易实现;
- ✓ 适用于大规模场景以及小物体的重建,能够处理复杂表面;
- ✓ 重建的效果依赖Delaunay Triangulation的质量,容易受到噪声和外点的影响;
- ✓ 通常需要结合Mesh refinement获取更加精细的表面细节。
常用的表面重建算法
- ✓ 泊松表面重建算法 http://hhoppe.com/proj/poissonrecon/
- ✓ Delaunay Triangualtion + Graph Cut https://github.com/cdcseacave/openMVS
- ✓ SSd 重建算法 http://mesh.brown.edu/ssd/paper.html
- ✓ FSSR 重建算法 http://www.regard3d.org/index.php/documentation/details/surface
参考
深蓝学院 基于图像的三维重建