第一章 神经网络是如何实现的
一个神经网络用不同的数据做训练,就可以识别不同的东西,那么神经网络究竟是怎么训练的?
三、神经网络是如何训练的?
1. 小朋友如何认识小动物?
- 小时候,每当看到一个小动物时,妈妈就会告诉我这是什么动物,见得多了,慢慢地就认识这些小动物了。

2. 建立数据集
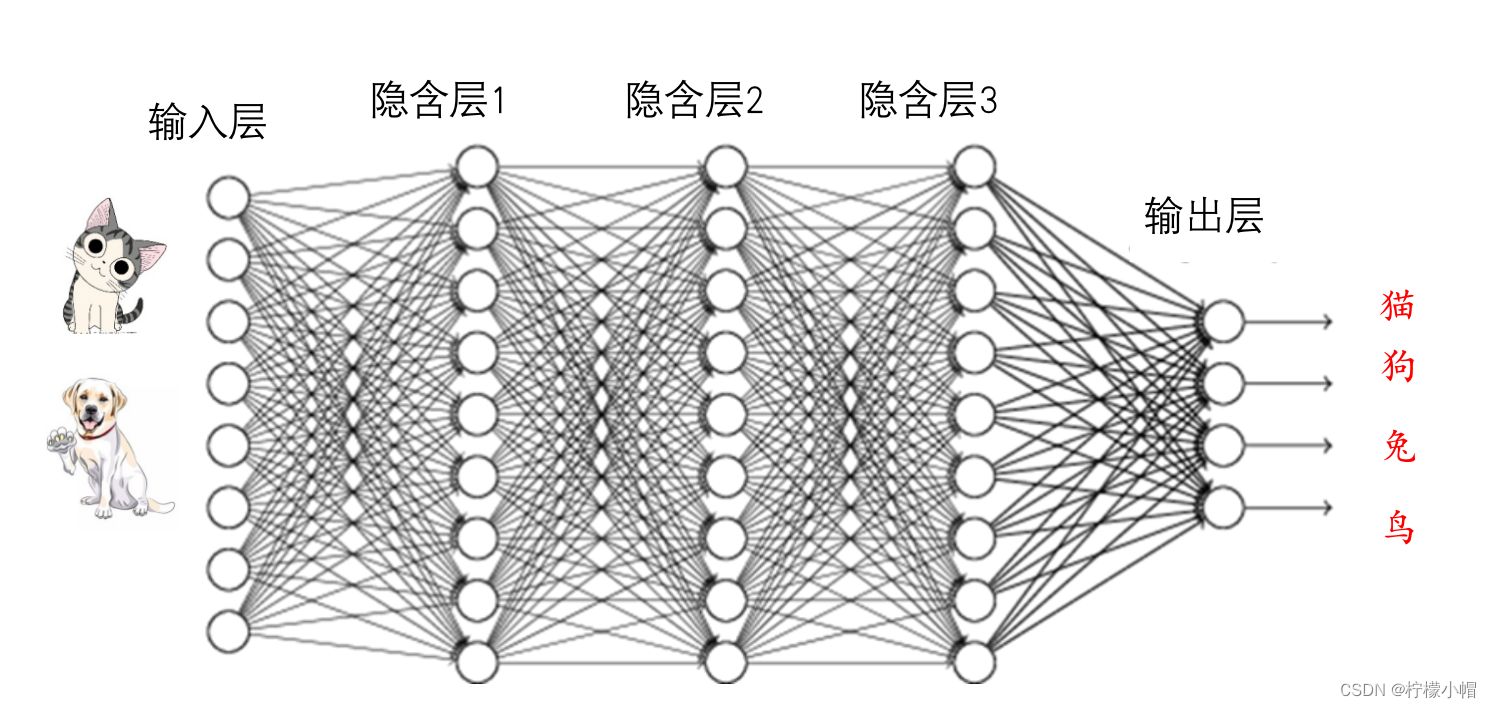
- 神经网络也是通过一个个样本认识动物的。人很聪明,见到一次猫,下次可能就认识这是猫了,但是神经网络有点笨,需要给他大量的样本才可能训练好。比如我们要建一个可以识别猫和狗两种动物的神经网络,首先需要收集大量的猫和狗的照片,不同品种、不同大小、不同姿势的照片都要收集,并标注好哪些照片是猫,哪些照片是狗,就像妈妈告诉你哪个是猫哪个是狗一样。这是训练一个神经网络的第一步,数据越多越好。其实我们人类有时候也会这么做。
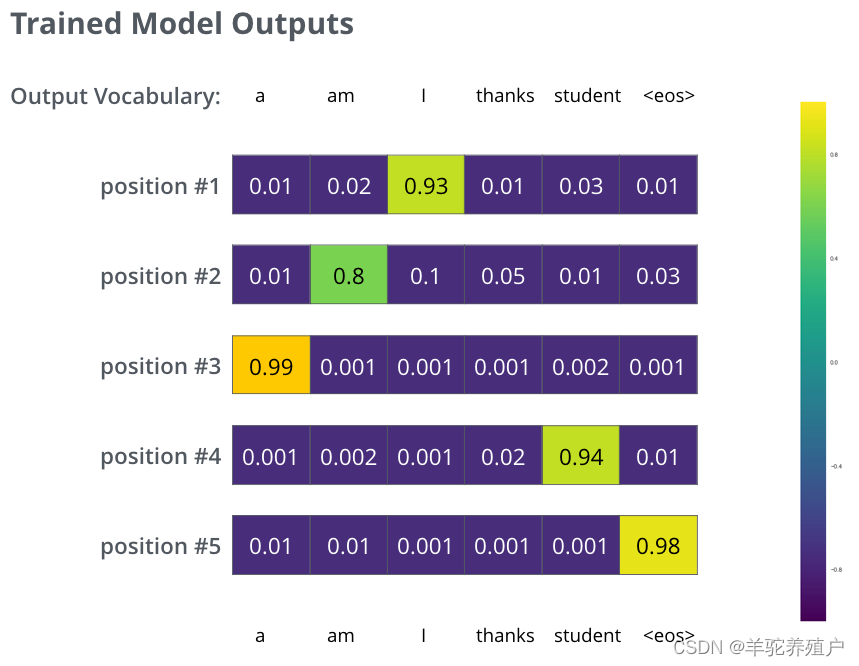
- 准备好数据之后,下一步就要进行训练了。所谓训练,就是调整神经网络的权重,使得当输入一个猫的照片时,猫对应的输出接近于1,狗对应的输出接近于0,而当输入一个狗的照片时,狗对应的输出接近于1,猫对应的输出接近于0。

3. 淋浴器示意图
- 我们每天是不是要洗澡?洗澡时,是怎么调节热水器的温度的?
- 热水器上有两个旋钮阀门,一个调节热水,一个调节冷水,如果感觉水热了,就调大冷水,如果感觉水冷了,就调大热水。
- 同时,感觉水热时也可以调小热水,感觉水冷也可以调小冷水。
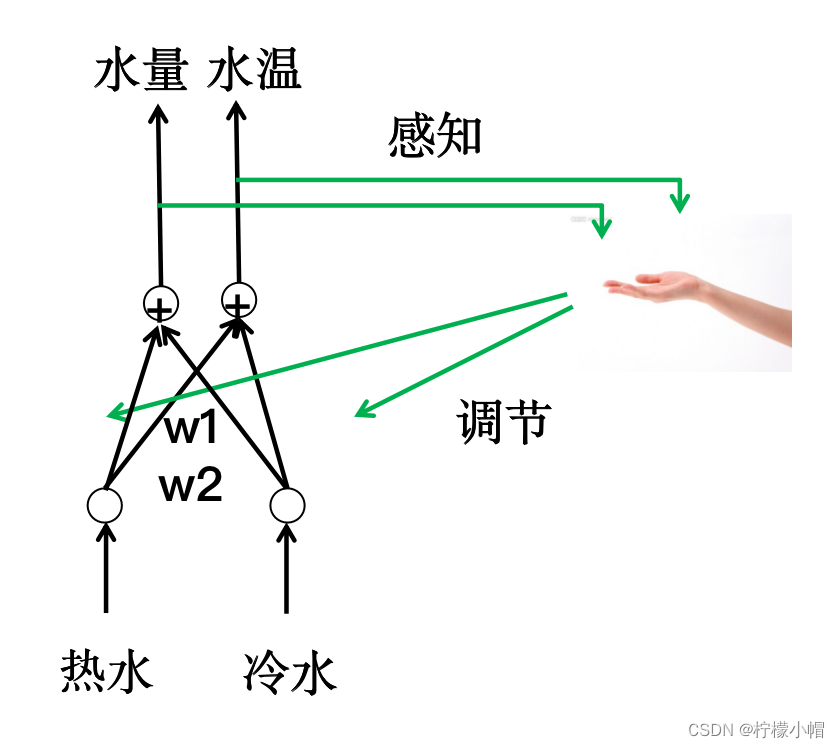
- 调整热水器温度有不同的方法,究竟调整哪个可能还需要看水量的大小。比如感觉水热了,但是水量也很大,这时就可以调节热水变小,如果水量不够大,则可以调节冷水变大。总之要根据水温和水量两个因素进行调节。
- 如果感觉水温与自己的理想温度差别比较大,就一次把阀门多调节一些,如果差别不大就少调节一些,经过多次调整之后,就可以得到比较理想的水温和水量了。
- 如何评价一个神经网络是否训练好了,这与训练神经网络是紧密相关的。在热水器的例子中,什么情况下会认为热水器调节好了?
- 如果觉得水温和水量跟希望的差不多,就认为调节好了。
- 但是对于计算机来说,什么叫差不多呢?需要有个衡量标准。
4. 如何评价调节效果?
-
我们用 t 水温 t_{水温} t水温表示希望设定的水温,而用 o 水温 o_{水温} o水温表示实际的水温,用 t 水量 t_{水量} t水量 表示希望的水量,用 o 水量 o_{水量} o水量表示实际的水量,这样就可以用希望值与实际值的误差来衡量是否“差不多”,即当误差比较小时,则认为水温和水量调节的差不多了。但是由于误差有可能是正的(实际值小于希望值时),也可能是负的(实际值大于希望值时),不方便使用,所以我们常常用输出的“误差平方和”作为衡量标准。如下式所示:
E ( 阀门 ) = ( t 水温 − o 水温 ) 2 + ( t 水量 − o 水量 ) 2 E_{(阀门)} = (t_{水温} - o_{水温})^2 + (t_{水量} - o_{水量})^2 E(阀门)=(t水温−o水温)2+(t水量−o水量)2 -
其中E是阀门大小的函数,通过适当调节冷、热水阀门的大小,就可以使得E取得比较小的值,当E比较小时,就认为热水器调节好了。这里的“阀门”就相当于神经网络的权值w。
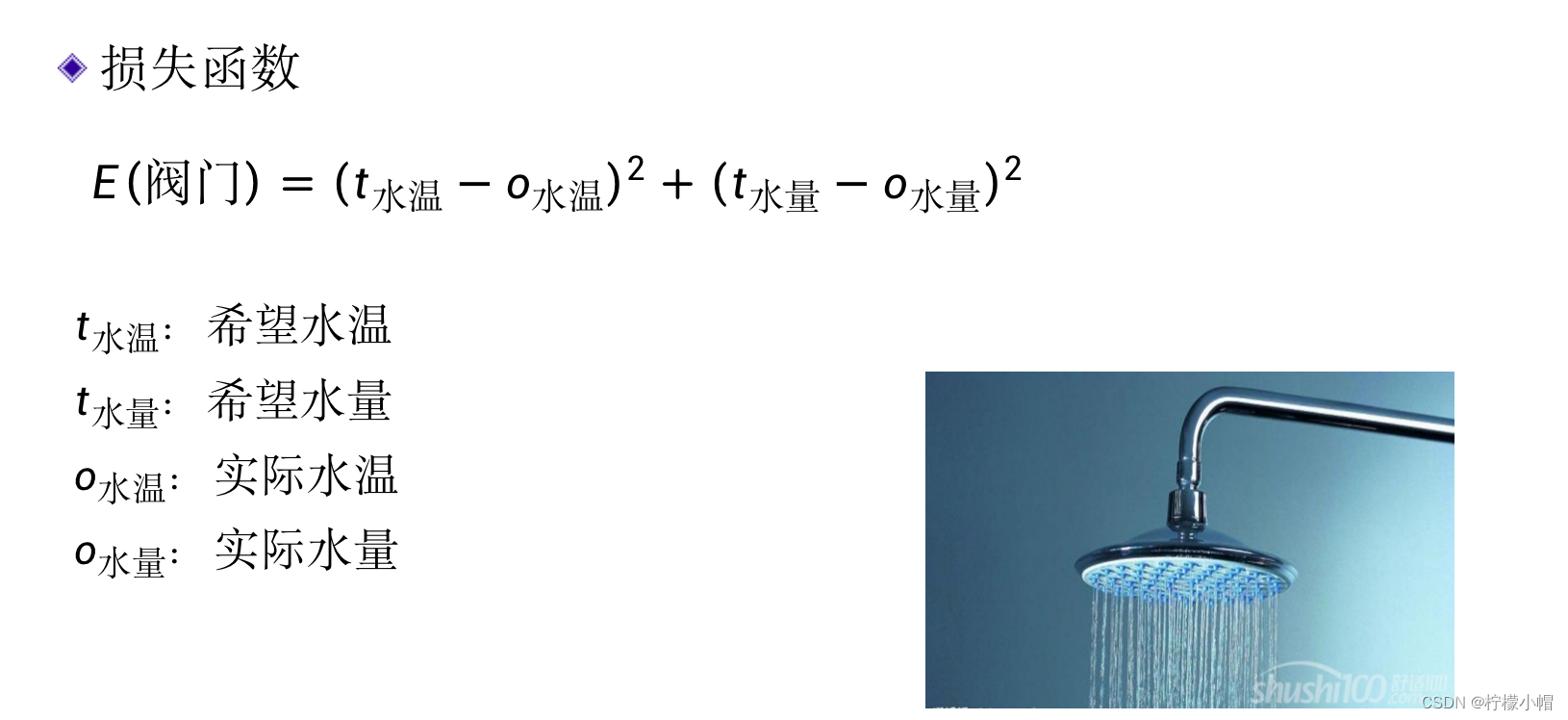
5. 损失函数 – 误差平方和
- 对于一个神经网络来说,我们假定有M个输出,对于一个输入样本d,用
o
k
d
(
k
=
1
,
2
,
⋯
,
M
)
o_{kd}(k=1,2,\cdots, M)
okd(k=1,2,⋯,M) 表示网络的M个实际输出值,这些输出值对应的目标输出值为
t
k
d
(
k
=
1
,
2
,
⋯
,
M
)
t_{kd}(k=1,2,\cdots, M)
tkd(k=1,2,⋯,M) ,对于该样本d神经网络输出的误差平方和可以表示为:
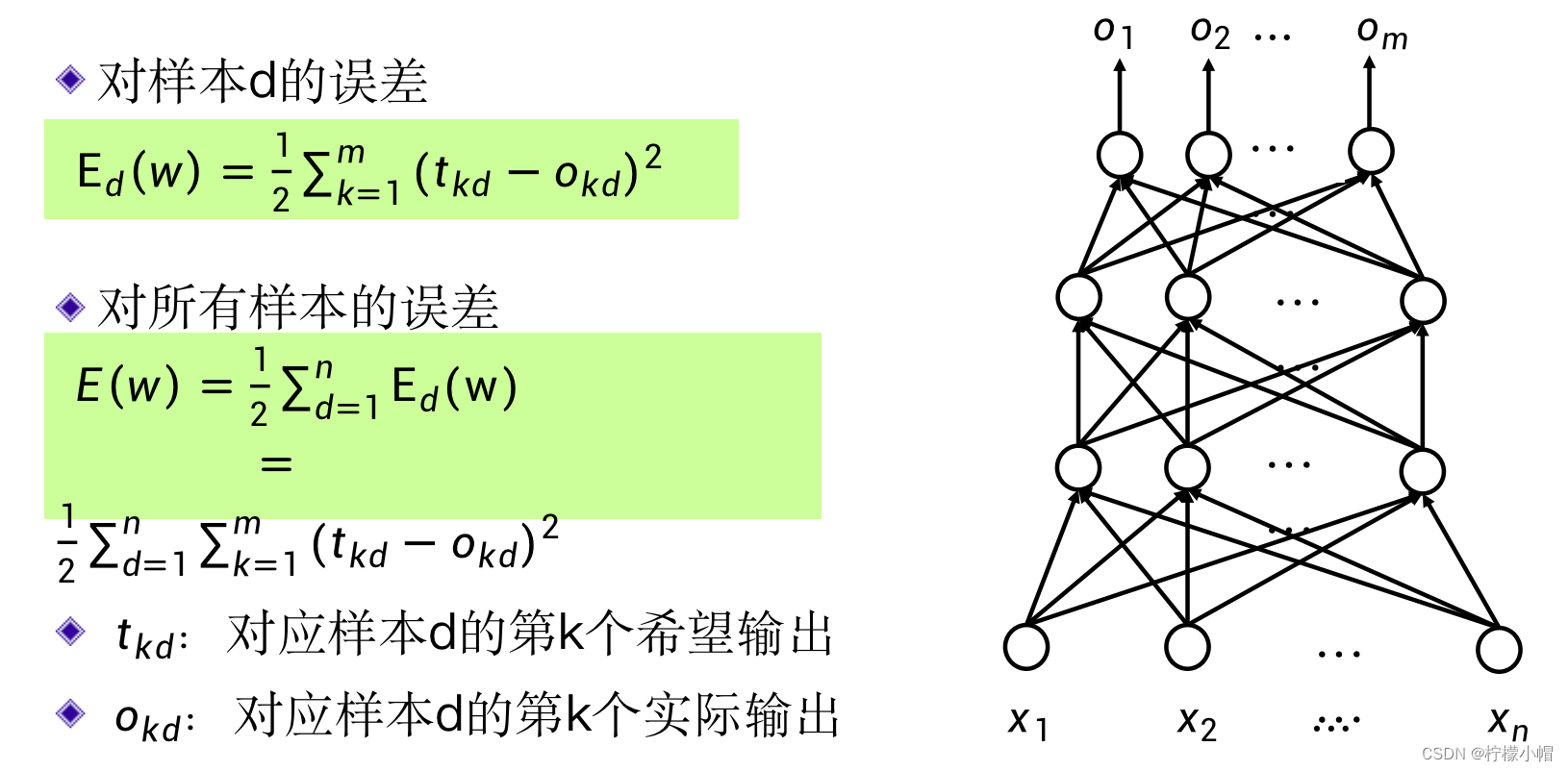
E d ( w ) = ∑ k = 1 M ( t k d − o k d ) 2 E_d(w) = \sum^{M}_{k=1}{(t_{kd} - o_{kd})^2} Ed(w)=k=1∑M(tkd−okd)2 - 这是对于某一个样本d的输出误差平方和,如果是对于所有的样本呢?只要把所有样本的输出误差平方和累加到一起即可,我们用E(w)表示:
E ( w ) = ∑ d = 1 N E d ( w ) = ∑ d = 1 N ∑ k = 1 N ( t k d − o k d ) 2 E(w) = \sum^{N}_{d=1}E_d(w) = \sum^{N}_{d=1} \sum^{N}_{k=1}{(t_{kd} - o_{kd})^2} E(w)=d=1∑NEd(w)=d=1∑Nk=1∑N(tkd−okd)2 - 这里的N表示样本的总数。我们通常称E(w)为损失函数,当然还有其他形式的损失函数,误差平方和只是其中的一个。这里的w是一个由神经网络的所有权重组成的向量。神经网络的训练问题,就是求得合适的权值,使得损失函数最小。
6. 如何训练?
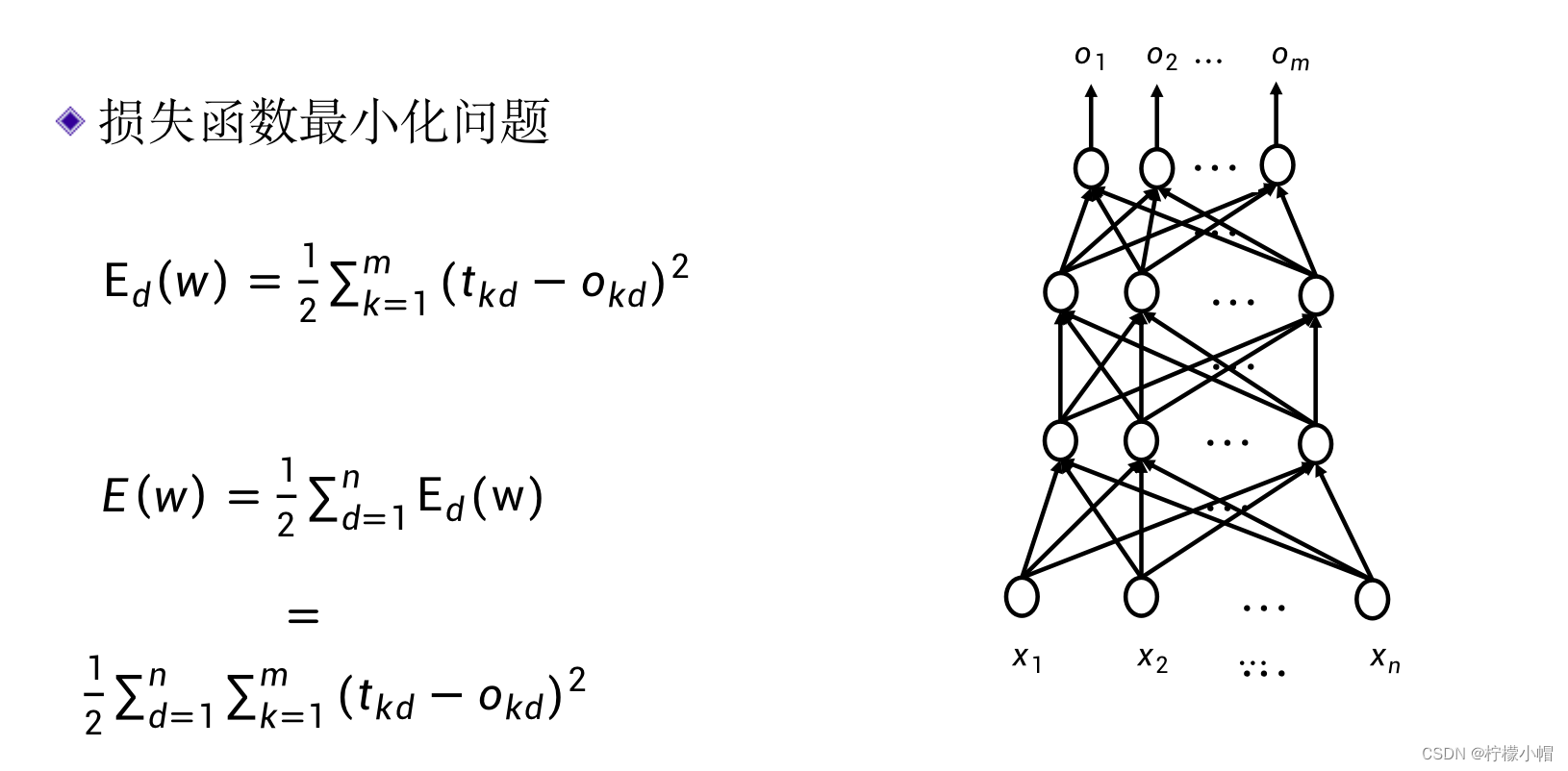
- 一个神经网络有那么多的权值,怎么求解?
7. 梯度下降法
7.1 简单例子
- 先从一个简单的例子说起,假定函数
f
(
θ
)
f(\theta)
f(θ) 如图所示 ,该函数只有一个变量
θ
\theta
θ,我们想求它的最小值,怎么计算呢?
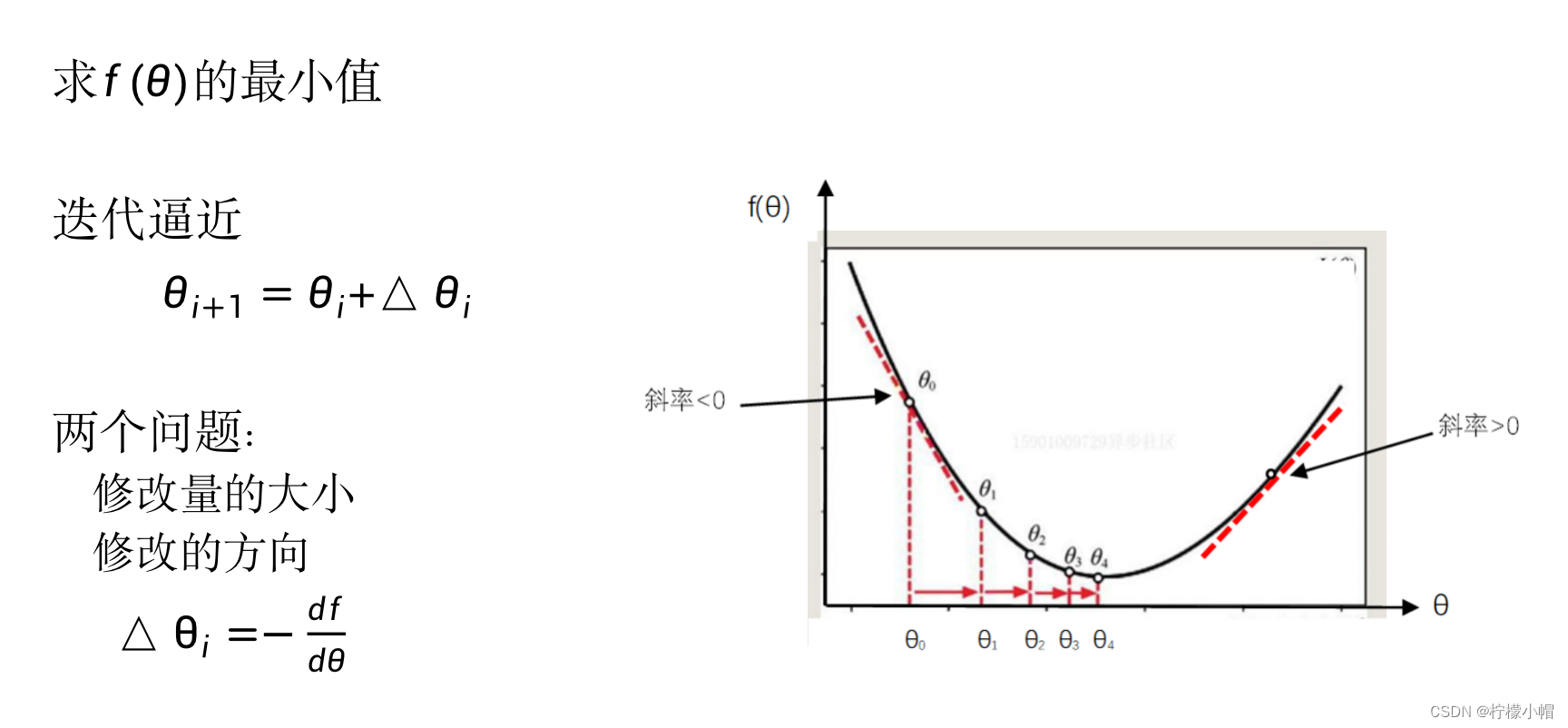
- 基本想法是,开始我们随机地取一个 θ \theta θ 值为 θ 0 \theta_0 θ0 ,然后对 θ 0 \theta_0 θ0 进行修改得到 θ 1 \theta_1 θ1 ,再对 θ 1 \theta_1 θ1 做修改得到 θ 2 \theta_2 θ2 ,这么一步步地迭代下去,使得 f ( θ i ) f(\theta_i) f(θi) 一点点接近最小值。
- 假设当前值为 θ i \theta_i θi ,对 θ i \theta_i θi 的修改量为 Δ θ i \Delta\theta_i Δθi ,则:
Δ θ i + 1 = θ i + Δ θ i \Delta\theta_{i+1} = \theta_i + \Delta\theta_i Δθi+1=θi+Δθi
- 如何计算 θ i \theta_i θi 呢?有两点需要确定:一个是修改量的大小,一个是修改的方向,即加大还是减少。
- 在图的两边距离最小值比较远的地方比较陡峭,而靠近最小值处则比较平缓,所以在没有其他信息的情况下,有理由认为,越是陡峭的地方距离最小值就越远,此处对 θ \theta θ 的修改量应该加大,而平缓的地方则说明距离最小值比较近了,修改量要比较小一些,以免越过最小值点。所以修改量的大小,也就是 θ i \theta_i θi 的绝对值,应该与该处的陡峭程度有关,越是陡峭修改量越大,而越是平缓则修改量越小。
7.2 导数度量
- 如何度量曲线某处的陡峭程度呢?
- 函数的导数,在某一点的导数就是曲线在该点切线的斜率,斜率的大小直接反应了该处的陡峭程度。可以用导数值作为曲线在某点陡峭程度的度量。
- 如何确定
θ
\theta
θ 的修改方向,也就是
θ
\theta
θ 是加大还是减小?
-
在某一点的导数就是曲线在该点切线的斜率,图的左半部分,曲线的切线是从左上到右下的,其斜率也就是导数值是小于0的负数,而在图的右半部分,曲线的切线是从左下到右上的,其斜率也就是导数值是大于0的正数。
-
左边的导数值是负的,这时 θ \theta θ 值应该加大,右边的导数值是正的,这时 θ \theta θ 值应该减小,这样才能使得θ值向中间靠近,逐步接近 f ( θ ) f(\theta) f(θ)取值最小的地方。所以, θ \theta θ 的修改方向刚好与导数值的正负号相反。因此,我们可以这样修改 θ i \theta_i θi 值:
Δ θ i + 1 = θ i + Δ θ i \Delta\theta_{i+1} = \theta_i + \Delta\theta_i Δθi+1=θi+Δθi
Δ θ i = − d f d θ \Delta\theta_i = - \frac{df}{d\theta} Δθi=−dθdf -
其中 − d f d θ -\frac{df}{d\theta} −dθdf 表示函数 f ( θ ) f(\theta) f(θ) 的导数。
-
7.3 步长
- 还有一个问题,如果导数值比较大可能会使得修改量过大,错过了最佳值,出现如图所示的“震荡”,降低了求解效率。
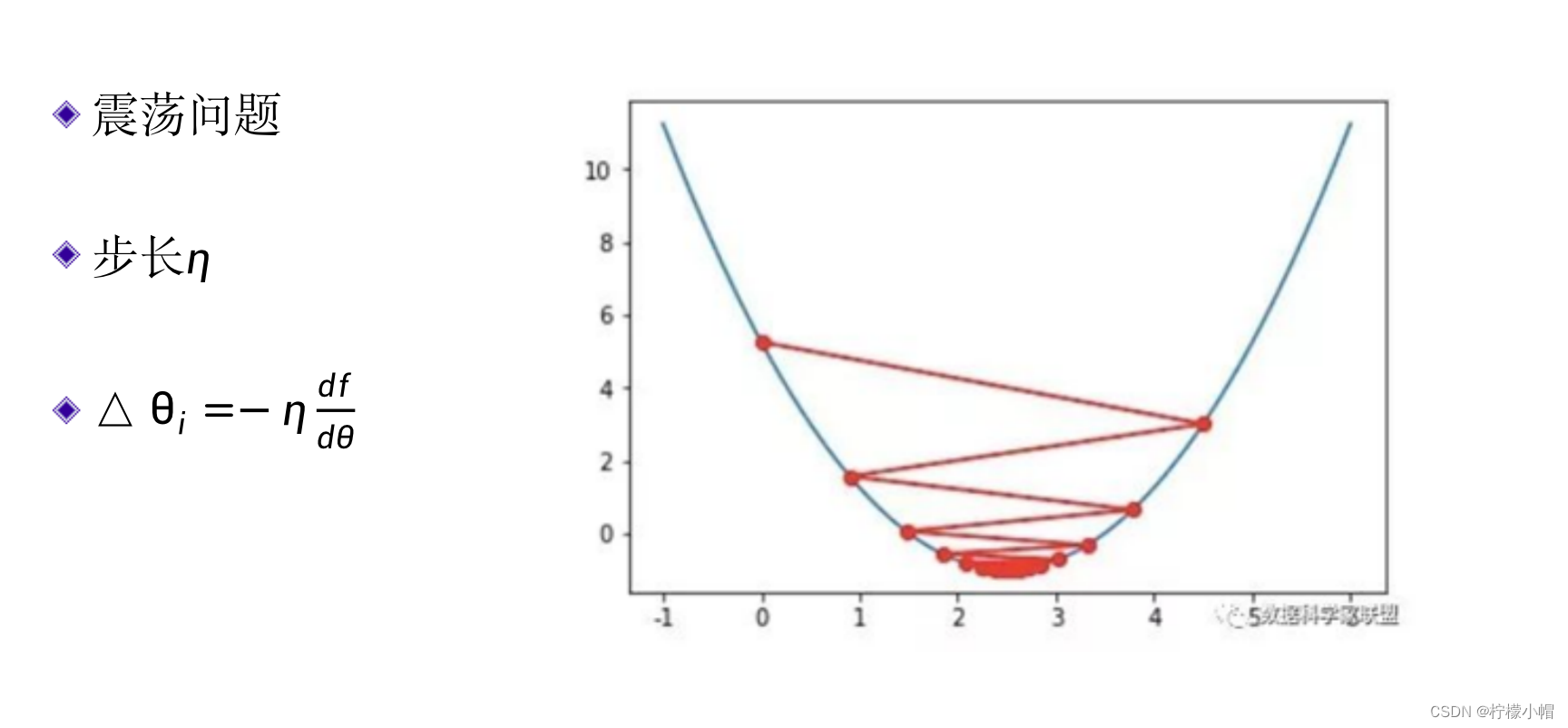
- 一种简单的处理办法是对修改量乘以一个叫做步长的常量η,这是一个小于1的正数,让修改量人为地变小。也就是:
Δ θ i = − η d f d θ \Delta\theta_i = - \eta\frac{df}{d\theta} Δθi=−ηdθdf - 步长η需要选取一个合适的值,往往根据经验和实验决定。
7.4 损失函数最小值
-
训练神经网络要优化的目标,就是求误差平方和的最小值,也就是损失函数E(w)的最小值。
-
我们可以用同样的方法求解E(w)的最小值,所不同的是E(w)是一个多变量函数,所有的权重都是变量,都要求解,每个权重的修改方式与前面讲的 θ \theta θ 的修改方式是一样的,只是导数要用偏导数代替。如果用 w i w_i wi 表示某个权重的话,则采用下式对权重 w i w_i wi 进行更新:
w i n e w = w i o l d + Δ w i w_i^{new} = w_i^{old} + \Delta w_i winew=wiold+Δwi
Δ w i = − η δ E ( w ) δ w i \Delta w_i = -\eta\frac{\delta E(w)}{\delta w_i} Δwi=−ηδwiδE(w) -
其中 w i o l d w_i^{old} wiold 、 w i n e w w_i^{new} winew 分别表示 w i w_i wi 修改前、修改后的值, δ E ( w ) δ w i \frac{\delta E(w)}{\delta w_i} δwiδE(w) 表示E(w)对 w i w_i wi 的偏导数。所有对 w i w_i wi 的偏导数组成的向量称为梯度,记作 ∇ w E ( w ) \nabla_wE(w) ∇wE(w) :
∇ w E ( w ) = [ δ E ( w ) δ w 1 , δ E ( w ) δ w 2 , ⋯ , δ E ( w ) δ w n ] \nabla_wE(w) = [ \frac{\delta E(w)}{\delta w_1},\frac{\delta E(w)}{\delta w_2}, \cdots, \frac{\delta E(w)}{\delta w_n} ] ∇wE(w)=[δw1δE(w),δw2δE(w),⋯,δwnδE(w)]
- 所以对所有w的修改,可以用梯度表示为:
w n e w = w o l d + Δ w w^{new} = w^{old} + \Delta w wnew=wold+Δw
Δ w = − η ∇ w E ( w ) \Delta w = -\eta \nabla_w E(w) Δw=−η∇wE(w) - 这里的 w o l d w^{old} wold 、 w n e w w^{new} wnew 、 Δ w \Delta_w Δw 、 ∇ w E ( w ) \nabla_w E(w) ∇wE(w) 均为向量, η \eta η 是常量。两个向量相加为对应元素相加,一个常量乘以一个向量,则是该常量与向量的每个元素相乘,结果还是向量。
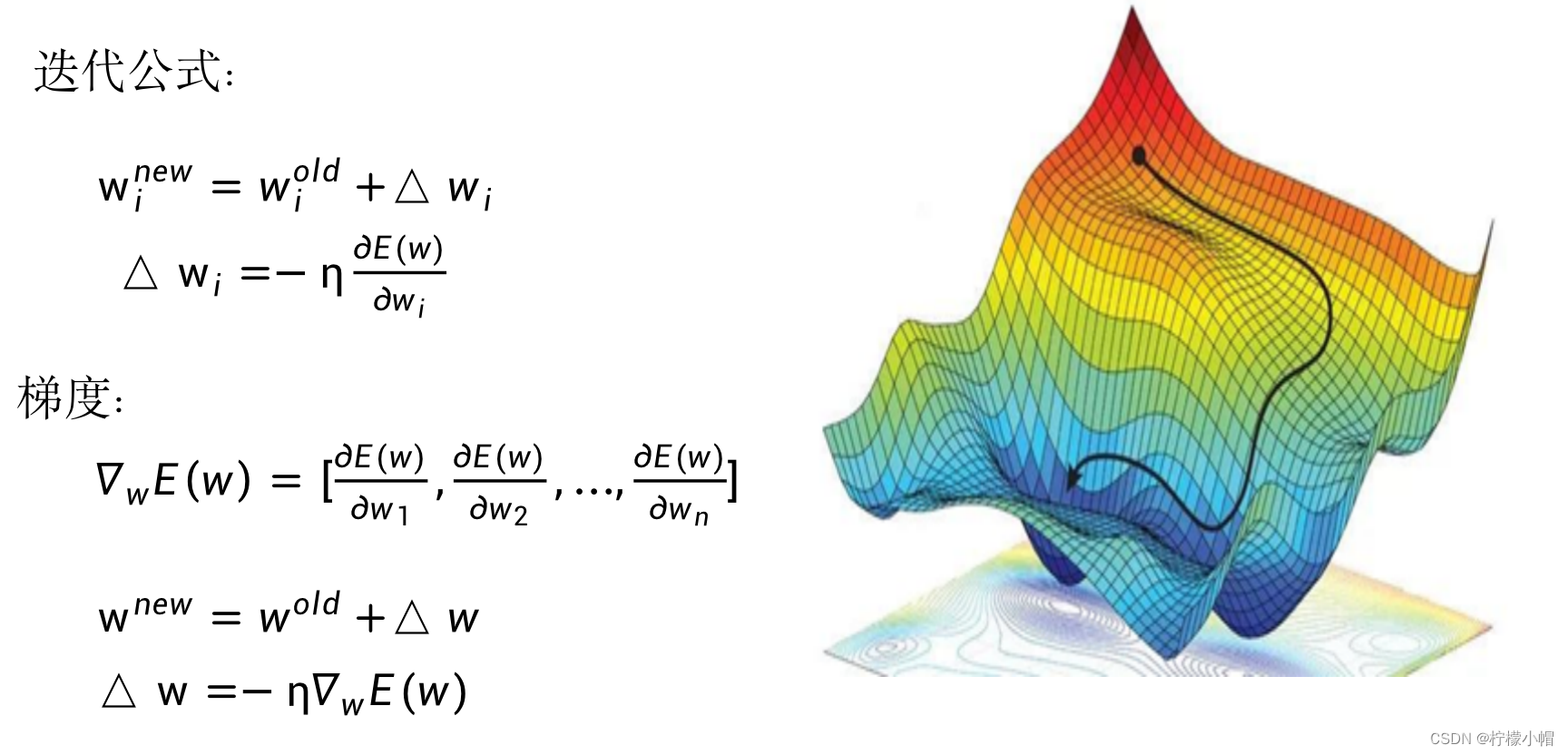
7.5 梯度物理含义
- 这里的梯度物理含义是什么呢?
- 如同只有一个变量时的导数表示函数曲线在某个点处的陡峭程度一样,梯度反应的是多维空间中一个曲面在某点的陡峭程度。就如同我们下山时,每次都选择我们当前站的位置最陡峭的方向一样。所以这种求解函数最小值的方法又称作梯度下降算法。
- 要训练神经网络,主要问题就是如何计算梯度。
7.6 梯度下降算法分类
- 对于神经网络来说,由于包含很多在不同层的神经元,计算梯度还是有些复杂的。在计算时,也分三种情况,一种是这里所说的标准梯度下降方法。在计算梯度时要用到所有的训练样本,一般来说训练样本量是很大的,每更新一次权重都要计算所有样本的输出,计算量会比较大。另一种极端的方法是,对每个样本都计算一次梯度,然后更新一次权重,这种方法称为随机梯度下降。由于每个样本都调整一次w的值,所以计算速度会比较快,一般情况下可以比较快地得到一个还不错的结果。在使用这个方法时,要求训练样本要随机排列,比如训练一个识别猫和狗的神经网络,不能前面都用猫训练,后面都用狗训练,而是猫和狗随机交错地使用,这样才可能得到一个比较好的结果。这也是随机梯度下降算法这一名称的由来。

- 一次只用一个样本会存在问题。随机梯度下降方法在训练的开始阶段可能下降的比较快,但在后期,尤其是接近最小值时,可能效果并不好,毕竟梯度是由一个样本计算得到的,并不能代表所有样本的梯度方向。另外就是可能有个别不好的样本,甚至标注错了的样本,会对结果产生比较大的影响。
- 介于用上全部样本和一次只用一个样本两种方法之间的一种方法是每次用一小部分样本计算梯度,修改权重w的值。这种方法称作小批量梯度下降算法,是目前用的最多的方法。
7.7 随机梯度下降算法介绍
-
利用随机梯度下降算法训练神经网络,就是求下式的最小值:
E d ( w ) = ∑ k = 1 M ( t k d − o k d ) 2 E_d(w) = \sum^{M}_{k=1}{(t_{kd} - o_{kd})^2} Ed(w)=k=1∑M(tkd−okd)2 -
其中d为给定的样本,M是输出层神经元的个数, t k d ( k = 1 , 2 , ⋯ , M ) t_{kd}(k=1,2,\cdots, M) tkd(k=1,2,⋯,M) 是样本d希望得到的输出值, o k d ( k = 1 , 2 , ⋯ , M ) o_{kd}(k=1,2,\cdots,M) okd(k=1,2,⋯,M) 是样本d的实际的输出值。
-
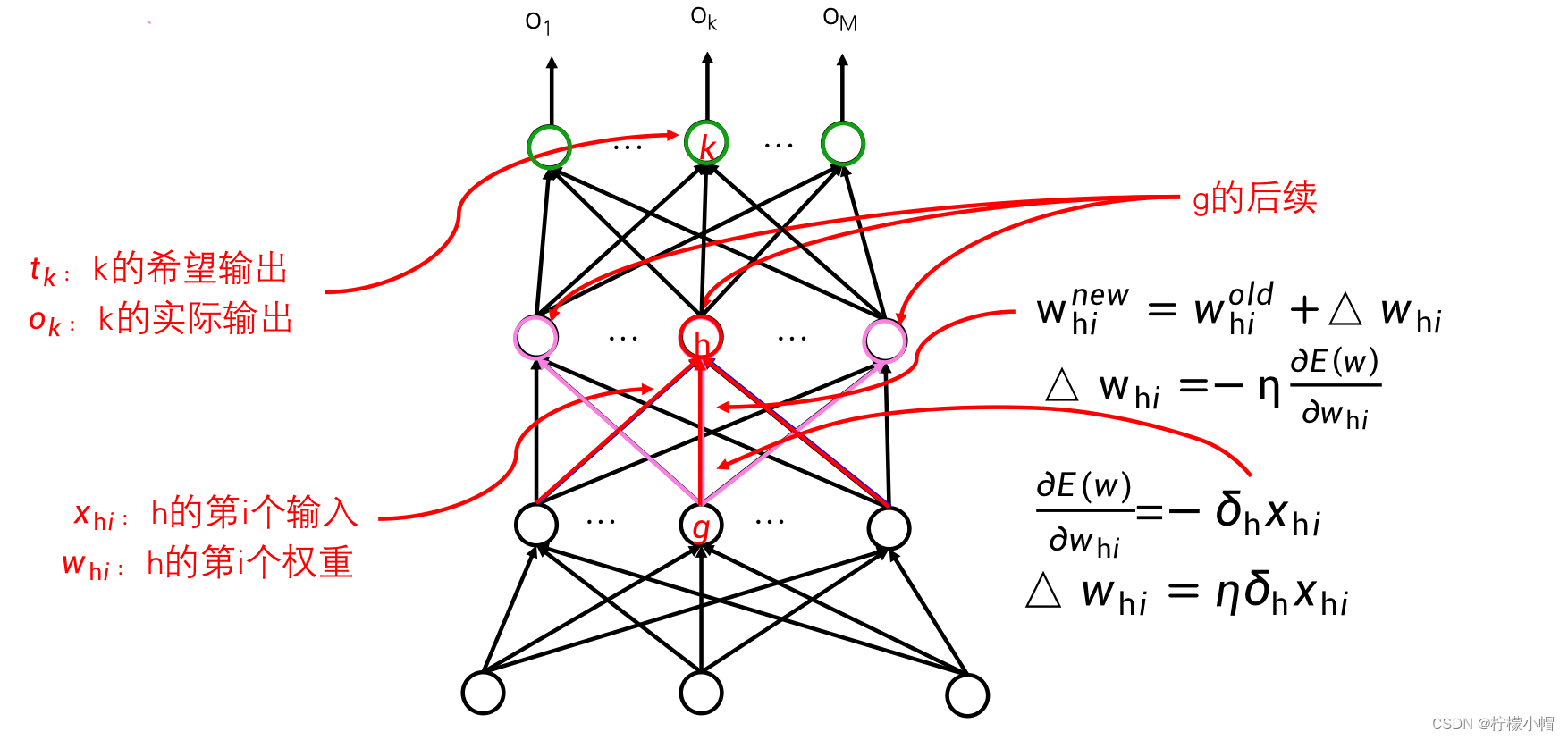
为了叙述方便,对于神经网络中的任意一个神经元j,我们约定如下符号:神经元j的第i个输入为 x j i x_{ji} xji ,相对应的权重为 w j i w_{ji} wji 。这里的神经元j可能是输出层的,也可能是隐含层的。 x j i x_{ji} xji不一定是神经网络的输入,也可能是神经元j所在层的前一层的第i个神经元的输出,直接连接到了神经元j。我们得到随机梯度下降算法如下。
7.8 随机梯度下降算法实现
-
神经网络的所有权值赋值一个比较小的随机值如[-0.05, 0.05]
-
在满足结束条件前:
- 对于每个训练样本,把样本输入神经网络,从输入层到输出层,计算每个神经元的输出
- 对于输出层神经元k,计算误差项:
δ k = ( t k − o k ) o k ( 1 − o k ) \delta_k = (t_k - o_k)o_k(1-o_k) δk=(tk−ok)ok(1−ok) - 对于隐含层神经元h,计算误差项:
δ h = o h ( 1 − o h ) ∑ k ∈ 后续 ( h ) δ k w k h \delta_h = o_h(1 - o_h)\sum_{k\in后续(h)}\delta_kw_{kh} δh=oh(1−oh)k∈后续(h)∑δkwkh
-
更新每个权值:
Δ w j i = η δ j x j i \Delta w_ji = \eta \delta_jx_{ji} Δwji=ηδjxji
w j i = w j i + Δ w j i w_{ji} = w_{ji} + \Delta w_{ji} wji=wji+Δwji -
其中算法第二行的结束条件,可以设定为所有样本中最大的 E d ( w ) E_d(w) Ed(w) 小于某个给定值时,或者所有样本中最大的 | Δ w j i \Delta w_{ji} Δwji| 小于给定值时,算法结束。
-
公式中的“ k ∈ 后续 ( h ) k\in后续(h) k∈后续(h)”的意思:
- h是隐含层的神经元,它的输出会连接到它的下一层神经元中
- “后续(h)”指的是所有的以h的输出作为输入的神经元,对于全连接神经网络来说,就是h所在层的下一层的所有神经元。
-
此行公式中:
∑ k ∈ 后续 ( h ) δ k w k h \sum_{k\in后续(h)}\delta_kw_{kh} k∈后续(h)∑δkwkh -
就是用h的每个后续神经元的误差项 δ k \delta k δk乘以h到神经元k的输入权重,再求和得到。
7.9 随机梯度下降算法总结
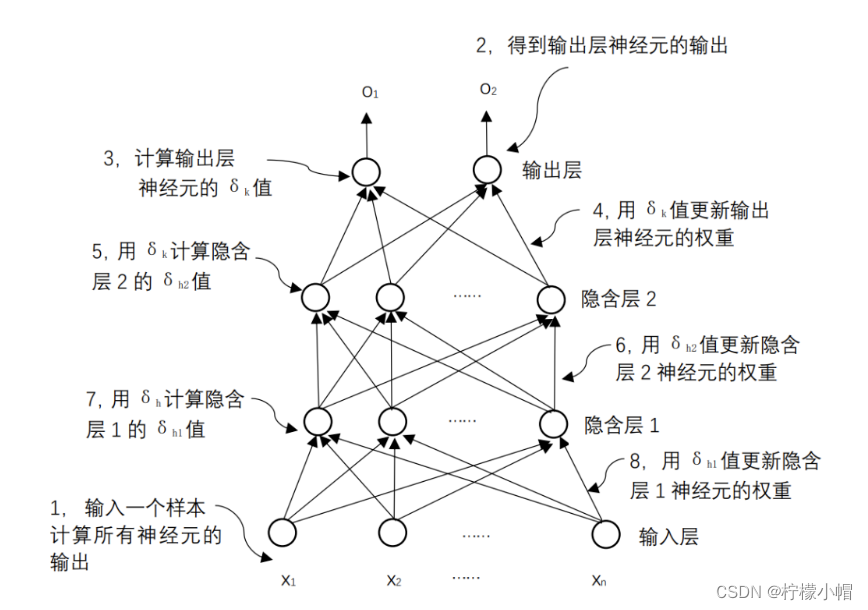
- 这个算法看起来像是从输出层开始,先计算输出层每个神经元的 δ \delta δ 值,有了 δ \delta δ 值,就可以对输出层神经元的权重进行更新。然后再利用输出层神经元的 δ \delta δ 值,计算其前一层神经元的 δ \delta δ ,这样就可以更新前一层的神经元的权重,这样一层层往前推,每次利用后一层的 δ \delta δ 值计算前一层的 δ \delta δ 值,就可以实现对所有神经元的权重更新了。
8. 符号说明
9. 反向传播算法(BP:Back Propagation)
- 又称作误差反向传播算法
- 给出了一种计算偏导数的方法
- 当给定一个训练样本后,先是利用当前的权重从输入向输出方向计算每个神经元的输出值,然后再从输出层开始反向计算每个神经元的δ值,从而对每个神经元的权重进行更新。如图所示。正是由于采用这样一种反向一层层向前推进的计算过程,所以它有个名称叫“反向传播算法”,简称BP(Backpropagation Algorithm)算法。该算法也是神经网络训练的基本算法,不只是可以训练全连接神经网络,到目前为止的任何神经网络都是采用这个算法,只是根据神经网络的结构不同,具体计算上有所差别。

10. BP 算法的条件
- 前面介绍的随机梯度算法中的具体计算方法,是在损失函数采用误差平方和,并且激活函数采用sigmoid函数这种特殊情况下推导出来的,如果用其他的损失函数,或者用其他的激活函数,其具体的计算方法都会有所改变,这一点一定要注意。

- 有多种不同的激活函数,那还有其他的损失函数吗?
11. 交叉熵损失函数
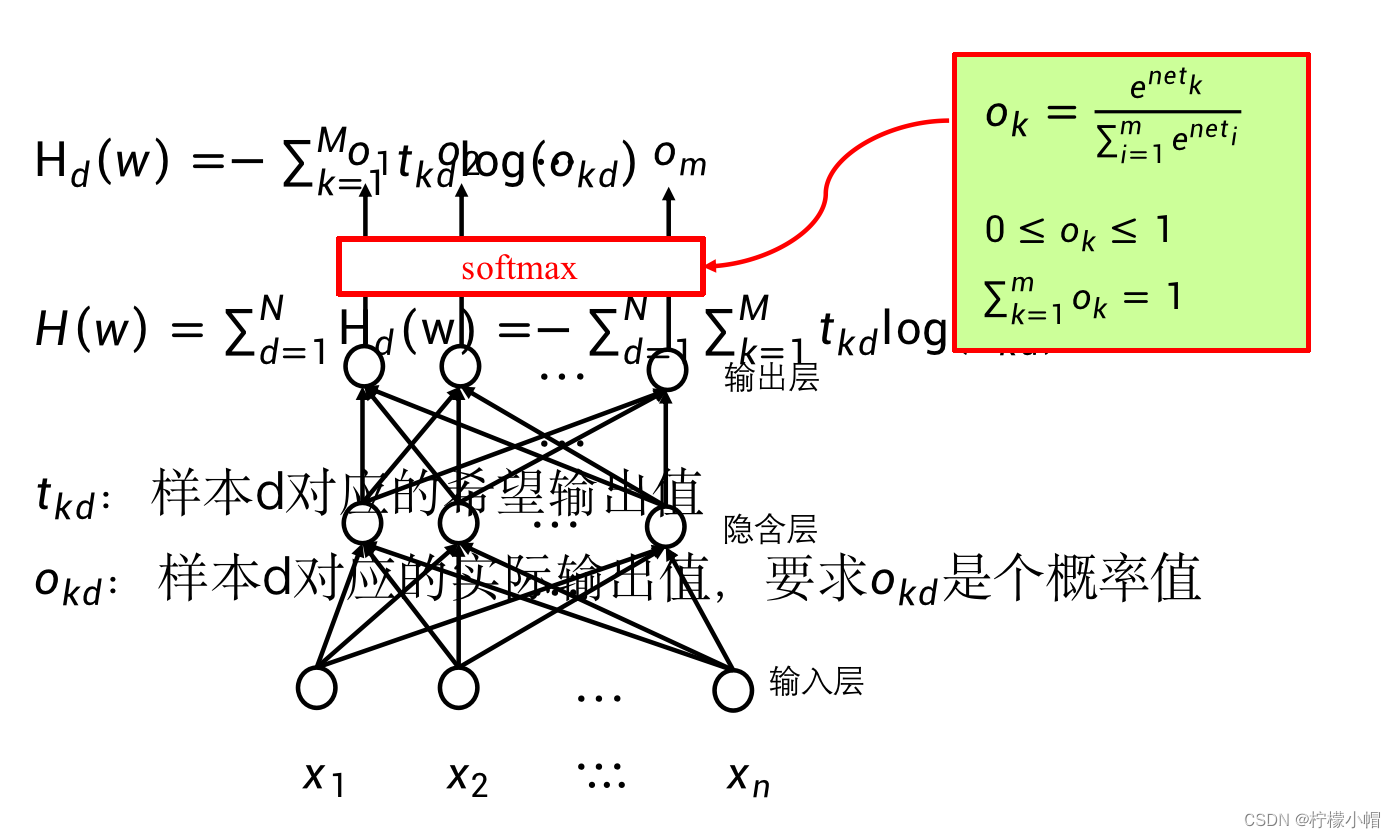
- 常用的损失函数:交叉熵损失函数
H d ( w ) = − ∑ k = 1 M t k d l o g ( o k d ) H_d(w) = -\sum^{M}_{k=1}t_{kd}log(o_{kd}) Hd(w)=−k=1∑Mtkdlog(okd) - 这是对于一个样本d的损失函数,如果是对于所有的样本,则为:
H ( w ) = − ∑ d = 1 N H d ( w ) = − ∑ d = 1 N ∑ k = 1 M t k d l o g ( o k d ) H(w) = -\sum^{N}_{d=1}H_d(w) = -\sum^{N}_{d=1}\sum^{M}_{k=1}t_{kd}log(o_{kd}) H(w)=−d=1∑NHd(w)=−d=1∑Nk=1∑Mtkdlog(okd) - 其中
t
k
d
t_{kd}
tkd 表示样本d在输出层第k个神经元的希望输出,
o
k
d
o_{kd}
okd 表示样本d在输出层第k个神经元的实际输出,
l
o
g
(
o
k
d
)
log(o_{kd})
log(okd) 表示对输出
o
k
d
o_{kd}
okd 求对数。
- 交叉熵损失函数具体的物理含义:
- 前面以猫、狗识别举例时,一个输出代表猫,一个输出代表狗。当输入为猫时,代表猫的输出希望为1,另一个希望为0,而当输入为狗时,则是代表狗的输出希望为1,另一个希望为0。这里的希望输出1或者0,可以认为就是概率值。
- 如何在神经网络输出层获得一个概率呢?
-
如果在输出层获得概率值,需要满足概率的两个主要属性,一个是取值在0和1之间,另一个是所有输出累加和为1。为此需要用到一个名为softmax的激活函数。该激活函数与前面介绍过的只作用于一个神经元的激活函数不同,softmax作用在输出层的所有神经元上。
-
设 n e t 1 、 ⋯ 、 n e t m net_1、\cdots 、 net_m net1、⋯、netm 分别为输出层每个神经元未加激活函数的输出,则经过softmax激活函数之后,第i个神经元的输出 o i o_i oi 为:
o i = e n e t i e n e t 1 + e n e t 2 + ⋯ + e n e t m o_i = \frac{e^{net_i}}{e^{net_1}+ e^{net_2}+ \cdots + e^{net_m}} oi=enet1+enet2+⋯+enetmeneti -
很容易验证这样的输出值可以满足概率的两个属性。这样我们就可以将神经网络的输出当作概率使用了,后面我们会看到这种用法非常普遍。
-
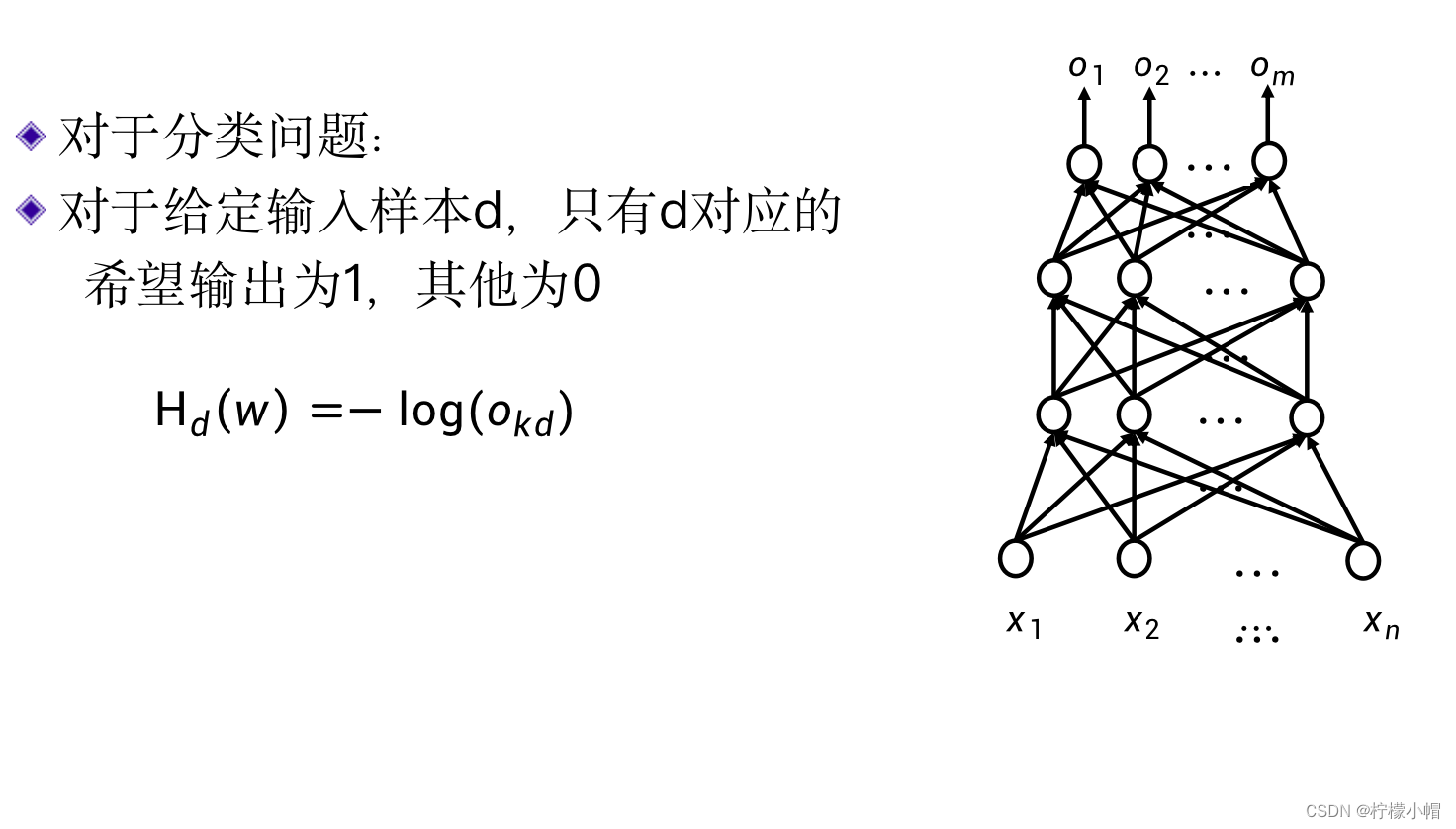
- 从概率的角度来说,我们就是希望与输入对应的输出概率比较大,而其他输出概率比较小。对于一个分类问题,当输入样本给定时,M个希望输出中只有一个为1,其他均为0,所以这时的交叉熵中求和部分实际上只有一项不为0,其他项均为0,所以:
H d ( w ) = − l o g ( o k d ) H_d(w) = -log(o_{kd}) Hd(w)=−log(okd) - 我们求 − l o g ( o k d ) -log(o_{kd}) −log(okd) 最小,去掉负号实际就是求 l o g ( o k d ) log(o_{kd}) log(okd) 最大,也就是求样本d对应输出的概率值 o k d o_{kd} okd 最大。由于输出层用的是softmax激活函数,输出层所有神经元输出之和为1,样本d对应的输出变大了,其他输出也就自然变小了。
- 误差平方和损失函数和交叉熵损失函数各有什么用处呢?
12. 两种损失函数的作用
-
从上面的分析看,交叉熵损失函数更适合于分类问题,直接优化输出的概率值。而误差平方和损失函数比较适合于预测问题。
-
如果输出是预测某个具有具体大小的数值,就是预测问题。比如说,我们根据今天的天气情况,预测明天的最高气温,就属于预测问题,因为我们预测的是气温的具体数值。

13. 总结

-
神经网络通过优化损失函数最小进行训练,损失函数有误差的平方和、交叉熵等损失函数。不同的损失函数应用于不同的应用场景,误差的平方和损失函数一般用于求解预测问题,交叉熵损失函数一般用于求解分类问题。
-
BP算法是神经网络常用的优化方法,来源于梯度下降算法。其特点是给出了一种反向传播计算误差的方法,从输出层开始,一层一层地计算误差,以便实现对权重的更新。
-
一次只使用一个样本的BP算法称为随机梯度下降算法,而一次使用若干个样本的BP算法称为批量梯度下降算法。批量梯度下降算法是更常用的神经网络优化算法。
-
BP算法是一个迭代过程,反复使用训练集中的样本对神经网络进行训练。训练集中的全部样本被使用一次称为一个轮次,一般需要多个轮次才能完成神经网络的训练。